Table of Contents
2. Balancing Forces and Torques
- 2.9 Cross products — torques
2.9 Cross products — torques

adapted from
rachaelvoorhees from arlington, va \ wikimedia CC BY 2.0}
The pictures in the margin show the sign of a seesaw,
a playground toy that works even for people with vastly different weight and size.
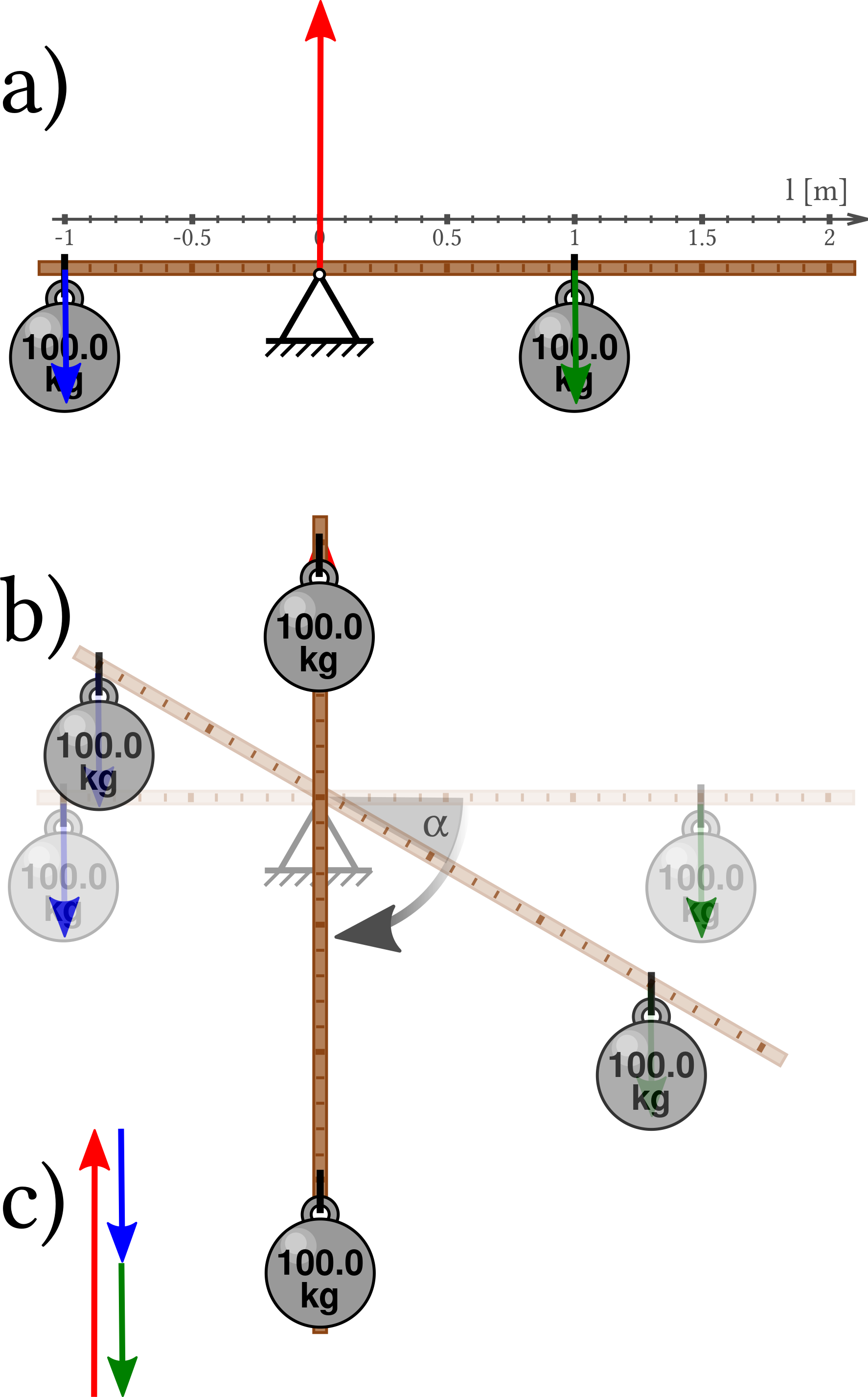
Figure 2.16a) shows a balanced scale.
When the forces acting on the scale do not add up to zero,
we pick up the scale.
It moves.
The according force balance for the beam of the scale is shown in Figure 2.16c).
In general the beam does not stay at rest,
when the two masses are not attached at the same distance from the fulcrum.
The force balance, Figure 2.16c), still hods,
and the beam turns, rather than being lifted.
The sum of attached forces tells us if an object is displaced.
In analogy we introduce the torque to describe whether it turns.
When the beam is vertical there is no torque,
and it takes its maximum when the beam is horizontal.
In the former case the forces act parallel to the beam,
and in the latter they act in orthogonal direction.
Moreover, a weight that is attached at a larger distance to the fulcrum induces a larger torque,
and the torque also increases with mass.
This is expressed in the lever rule.
based on from Jahobr/wikimedia
CC0 1.0
a) The lever is balanced when two equal masses are attached at the same distance from the fulcrum.
b) It is at (stable) rest only in a single position when equal weighs are attached at different distances.
c) In all positions the sum of the forces on the beam, by the fulcrum and by the two weights, add to zero.
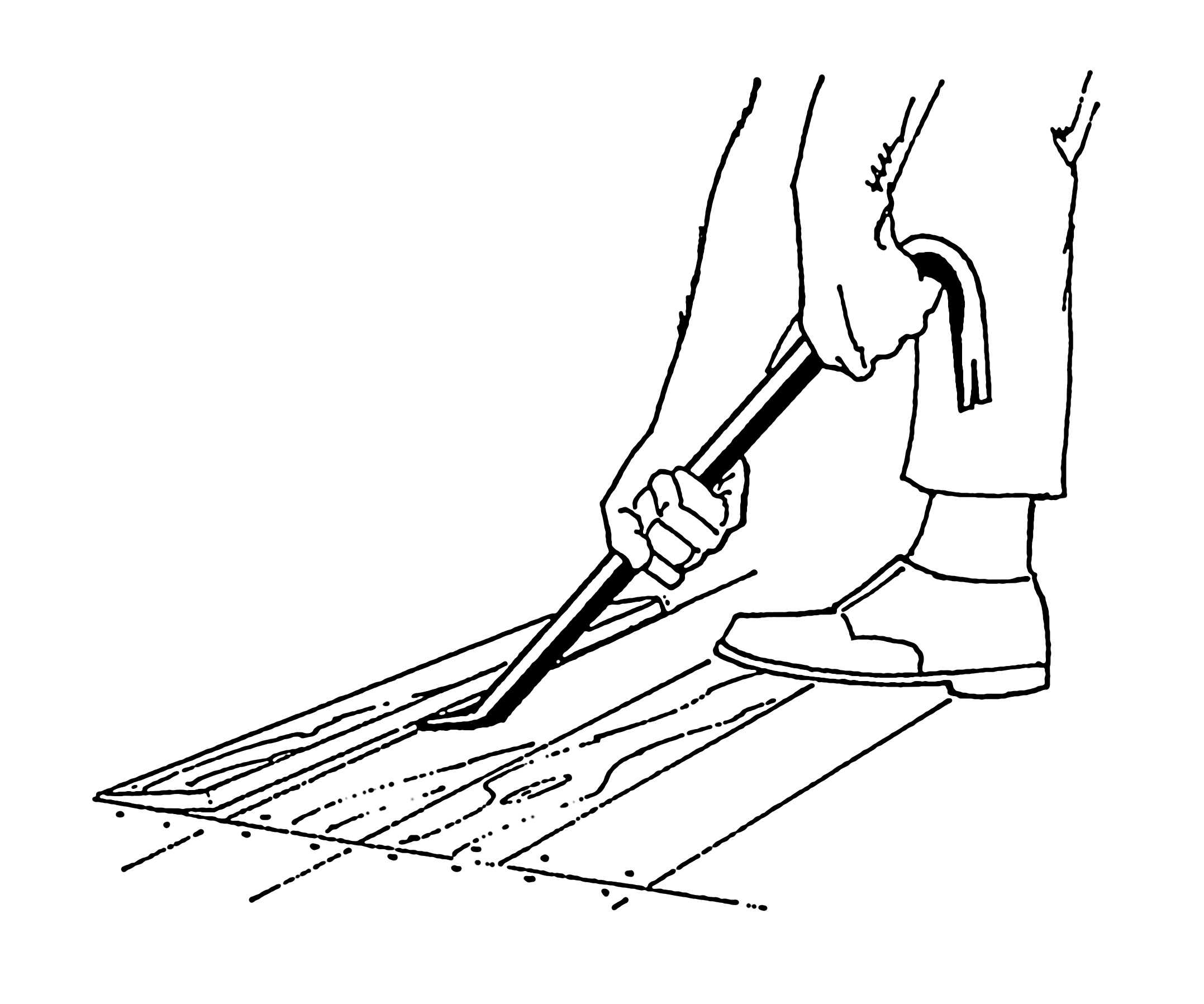
Pearson Scott Foresman / Public domain}
Figure 2.17: Action of a crowbar.

Mechanic’s Magazine cover of Vol II, Knight \& Lacey, London, 1824./wikipedia, public domain
Figure 2.18: Illustration of Archimedes' remark about moving the earth.
Example 2.23 Torques on a Lever
The torque $T$ exerted by a lever is given by the product, $T = l \, F$,
of the modulus of the force $F$ acting vertical to the lever
and the distance $l$ between the fulcrum and the point where the force is applied,
which is called length of the lever arm.
When several forces act on the same lever,
then the total torque amounts to the sum of the torques induced by the individual forces,
$T = \sum_i l_i \, F_i$.
For the scale in Figure 2.16a) and b) we find
\begin{align*}
T_a &= (1\text{m}) \; (100\text{kg}) \, (-g)
+ (-1\text{m}) \; (100\text{kg}) \, (-g)
= 0
\\
T_b &= (1.5\text{m}) \; (100\text{kg}) \, (-g) \, \cos\alpha
+ (-1\text{m}) \; (100\text{kg}) \, (-g) \, \cos\alpha
\\
&\simeq -500 \, \cos\alpha \: \text{kg m$^2$/s$^2$}
\end{align*}
The torque vanishes only when $\alpha = \pi/2$ as shown in the figure,
and for the unstable tipping point $\alpha=-\pi/2$.
Remark 2.26 Adopting a lever where force is applied on a long arm allows one to move very heavy objects or break very stable objects. Common technological applications are the crowbar and the lever. Archimedes was so impressed by this principle that he is quoted to have remarked “Δοσ μοι που στω και κινω την γην” (Archimedes, 1878), i.e. ``Give me but one firm spot on which to stand, and I will move the earth'' (Oxford Dictionary of Quotations, 1953)
Observe the sign of the torque:
In Example 2.23 it is positive for counterclockwise motion,
and negative for clockwise motion.
The axis of rotation is fixed by the fulcrum.
However, when acting the crowbar, one applies a horizontal force to get the crowbar under the obstacle.
This induces a rotation around a vertical axis.
Subsequently, a vertical force is applied to lift the obstacle.
It induces a rotation around a horizontal axes.
The relation between the directions of
the lever arm,
the force,
and the rotation axis is commonly illustrated by the right-hand rule
(Figure 2.19):
Here the arm points in the direction of the lever arm,
the fingers in the direction of the applied force,
and the thump along the rotation axis.
This suggests to define torque as a product of two vectors,
the arm $\mathbf\ell$ and the force $\mathbf F$
that provide the torque, $\mathbf T$,
which is a vector of length $|\mathbf\ell| \: |\mathbf F| \: \sin\angle{\mathbf\ell, \mathbf F}$
in a direction normal to the plane defined by $\mathbf\ell$ and $\mathbf F$.
This operation, $\mathbf T = \mathbf\ell \times \mathbf F$ defines the cross product.
We explore its properties in a mathematical digression.
2.9.1 Algebraic properties of cross products
Definition 2.14 Cross product on $\mathbb{R}^3$
The cross product on the vector space $\mathbb{R}^3$ defines a binary operation
$\times : \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}^3$
with the following properties for $\mathbf u, \mathbf v, \mathbf w \in \mathbb{R}^3$ and $c \in \mathbb{R}$
- anti-commutativity: $\mathbf u \times \mathbf v = - \mathbf v \times \mathbf u$
- distributivity: $\mathbf u \times ( \mathbf v + \mathbf w ) = \mathbf u \times \mathbf v + \mathbf u \times \mathbf w$
- compatibility with scalar multiplication: $(c\, \mathbf u) \times \mathbf v = \mathbf u \times (c\, \mathbf v) = c \, (\mathbf u \times \mathbf v)$
- symmetry of scalar triple product (Jacobi identity): $\mathbf u \cdot (\mathbf v \times \mathbf w) = \mathbf v \cdot (\mathbf w \times \mathbf u) = \mathbf w \cdot (\mathbf u \times \mathbf v)$
Moreover for every right-handed set of three orthonormal vectors $\mathbf e_1$, $\mathbf e_2$, and $\mathbf e_3$ we require
- normalization: $\mathbf e_1 \cdot (\mathbf e_2 \times \mathbf e_3) = 1$
 Schorschi2 at de.wikipediaderivative work: Wizard191, public domain
Schorschi2 at de.wikipediaderivative work: Wizard191, public domain
Figure 2.19: Right-hand rule.
Remark 2.27 The cross product of a vector with itself vanishes \begin{align*} \forall \mathbf v \in\mathbb{R}^3 : \mathbf v \times \mathbf v = \mathbf 0 \end{align*}
Proof. Vanishing of $\mathbf v \times \mathbf v$ is a consequence of anti-commutativity: \begin{align*} \mathbf v \times \mathbf v = - \mathbf v \times \mathbf v \quad\Rightarrow 2 \: \mathbf v \times \mathbf v = \mathbf 0 \quad\Rightarrow \mathbf v \times \mathbf v = \mathbf 0 \\ \end{align*}
Theorem 2.4 Right-handed orthonormal basis in $\mathbb{R}^3$
Let $\mathbf e_1, \mathbf e_2 \in \mathbb{R}^3$ be orthonormal vectors, $\mathbf e_1 \cdot \mathbf e_2 = \delta_{12}$.
Then $\mathbf e_1$, $\mathbf e_2$, and $\mathbf e_3=\mathbf e_1 \times \mathbf e_2$
form a right-handed orthonormal basis for $\mathbb{R}^3$,
and we have
\begin{align*}
\mathbf e_i \cdot ( \mathbf e_j \times \mathbf e_k)
= \left\{ \begin{array}{rll}
1 & \quad\text{for } & ijk \in\{ 123, 231, 312 \} \\
-1 & \quad\text{for } & ijk \in\{ 132, 213, 321 \} \\
0 & \quad\text{else}
\end{array} \right.
\end{align*}
Remark 2.28 (Levi-Civita tensor $\varepsilon_{ijk}$)
It is convenient to introduce the abbreviation $\varepsilon_{ijk}$ for
\begin{align*}
\varepsilon_{ijk} =
\left\{
\begin{array}{rll}
1 & \quad\text{for } & ijk \in\{ 123, 231, 312 \} \\
-1 & \quad\text{for } & ijk \in\{ 132, 213, 321 \} \\
0 & \text{ else }
\end{array}
\right.
\end{align*}
This symbol is denoted as Levi-Civita tensor $\varepsilon_{ijk}$. With this symbol the relations between right-handed orthogonal unit vectors of a basis can more concisely be written as
\begin{align*}
\mathbf e_i \cdot ( \mathbf e_j \times \mathbf e_k ) = \varepsilon_{ijk}
\end{align*}
Moreover, it immediately provides the following representation of the scalar triple product $\mathbf u \cdot ( \mathbf v \times \mathbf w)$ in terms of coordinates $u_i$, $v_j$, $w_k$, $i,j,k \in\{1,2,3\}$,
\begin{align*}
\left.
\begin{array}{ll}
\mathbf u &= \sum_{i=1}^3 u_i \, \mathbf e_i \\
\mathbf v &= \sum_{j=1}^3 v_j \, \mathbf e_j \\
\mathbf w &= \sum_{k=1}^3 w_k \, \mathbf e_k
\end{array}\right\}
\quad\Rightarrow\quad
\mathbf u \cdot ( \mathbf v \times \mathbf w) = \sum_{i,j,k=1}^3 \varepsilon_{ijk} \, u_i \, v_j \, w_k
\end{align*}
or even $\mathbf u \cdot ( \mathbf v \times \mathbf w) = \varepsilon_{ijk} \, u_i \, v_j \, w_k$ with Einstein notation. The symmetry of the triple scalar product is an immediate consequence of the symmetry of the $\varepsilon$-tensor.
Proof.
The identity $\mathbf u \cdot ( \mathbf v \times \mathbf w) = \varepsilon_{ijk} \, u_i \, v_j \, w_k$
follows from the compatibility with scalar product and the relation for the basis vectors
$\mathbf e_i \cdot ( \mathbf e_j \times \mathbf e_k)$.
The details of the proof are given as Problem 2.23.
Proof of Theorem 2.4
We show that $\mathbf e_1$, $\mathbf e_2$, and $\mathbf e_3=\mathbf e_1 \times \mathbf e_2$ form three orthonormal vectors.
By assumption $\mathbf e_1$ and $\mathbf e_2$ are orthonormal.
Hence, we show that $\mathbf e_3$ is a unit vector that is orthogonal to $\mathbf e_1$ and $\mathbf e_3$:
\begin{align*}
\mathbf e_1 \cdot \mathbf e_3
&= \mathbf e_1 \cdot (\mathbf e_1 \times \mathbf e_2)
= \mathbf e_2 \cdot (\mathbf e_1 \times \mathbf e_1)
= \mathbf e_2 \cdot \mathbf 0 = 0
\end{align*}
\begin{align*}
\mathbf e_2 \cdot \mathbf e_3
&= \mathbf e_2 \cdot (\mathbf e_1 \times \mathbf e_2)
= \mathbf e_1 \cdot (\mathbf e_2 \times \mathbf e_2)
= \mathbf e_1 \cdot \mathbf 0 = 0
\end{align*}
\begin{align*}
\mathbf e_3 \cdot \mathbf e_3
&= \mathbf e_3 \cdot (\mathbf e_1 \times \mathbf e_2)
= \mathbf e_1 \cdot (\mathbf e_2 \times \mathbf e_3)
= 1
\end{align*}
Remark 2.29 (bac-cab rule) The double cross product can be expressed in terms of scalar products. Commonly this relation is stated in terms of three vectors $\mathbf a$, $\mathbf b$, and $\mathbf c \in \mathbb{R}^3$, \begin{align*} \mathbf a \times (\mathbf b \times \mathbf c) = \mathbf b \: (\mathbf a \cdot \mathbf c) - \mathbf c \: ( \mathbf a \cdot \mathbf b ) \end{align*} and referred to as bac-cab rule.
Proof.
We express the three vectors in terms of their coordinates with respect to the orthonormal basis
$\mathbf e_1$, $\mathbf e_2$, $\mathbf e_3$,
\begin{align*}
\mathbf a = \sum_{i=1}^3 a_i \, \mathbf e_i \quad
\mathbf b = \sum_{j=1}^3 b_j \, \mathbf e_j \quad
\mathbf c = \sum_{k=1}^3 c_k \, \mathbf e_k \quad
\text{with } a_i, b_j, c_k \in \mathbb{R}
\end{align*}
and use the rules defining the cross products and inner products
\begin{align*}
\mathbf a \times (\mathbf b \times \mathbf c)
&= \left( \sum_{i=1}^3 a_i \, \mathbf e_i \right) \times
\left[ \left( \sum_{j=1}^3 b_j \, \mathbf e_j \right) \times \left( \sum_{k=1}^3 c_k \, \mathbf e_k \right) \right]
\\
&= \sum_{i,j,k=1}^3 a_i \, b_j \, c_k \mathbf e_i \times ( \mathbf e_j \times \mathbf e_k )
\end{align*}
When $j=k$ or when $j$ and $k$ are both different from $i$ then the summand vanishes due to Remark 2.27.
For $i=j \neq k$ one has $\mathbf e_i \times ( \mathbf e_j \times \mathbf e_k ) = -\mathbf e_k$,
and for $i=k \neq j$ one has $\mathbf e_i \times ( \mathbf e_j \times \mathbf e_k ) = \mathbf e_j$.
Consequently,
\begin{align*}
\mathbf a \times (\mathbf b \times \mathbf c)
&= \sum_{i,k=1}^3 a_i \, b_i \, c_k (-\mathbf e_k)
+ \sum_{i,j=1}^3 a_i \, b_j \, c_i (\mathbf e_j)
\\
&= \mathbf b \: (\mathbf a \cdot \mathbf c) - \mathbf c \: ( \mathbf a \cdot \mathbf b )
\\
\end{align*}
Remark 2.30 (Jacobi identity) The cross product obeys the Jacobi identity: \begin{align*} \mathbf u \times (\mathbf v \times \mathbf w) + \mathbf v \times (\mathbf w \times \mathbf u) + \mathbf w \times (\mathbf u \times \mathbf v) = \mathbf 0 \end{align*}
Proof.
This can be verified by evaluating the triple cross products by the bac-cab rule.
Details are give as Problem 2.24.
Remark 2.31 In coordinate notation the cross product takes the form \begin{align*} \mathbf a \times \mathbf b = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \times \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} = \begin{pmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix} \end{align*}
Proof. For component $k$ of $\mathbf a \times \mathbf b$ we have \begin{align*} [ \mathbf a \times \mathbf b ]_k &= \hat{\boldsymbol e}_k \cdot ( \mathbf a \times \mathbf b ) = \hat{\boldsymbol e}_k \cdot \left[ \left( \sum_{i=1}^3 a_i \, \hat{\boldsymbol e}_i \right) \times \left( \sum_{j=1}^3 b_j \, \hat{\boldsymbol e}_j \right) \right] \\ &= \sum_{i,j=1}^3 a_i \, b_j \;\; \hat{\boldsymbol e}_k \cdot \left[ \hat{\boldsymbol e}_i \times \hat{\boldsymbol e}_j \right]_k = \sum_{i,j=1}^3 a_i \, b_j \; \varepsilon_{ijk} \end{align*} In the remark this is explicitly written out for $k\in\{1,2,3\}$.
2.9.2 Geometric interpretation of cross products
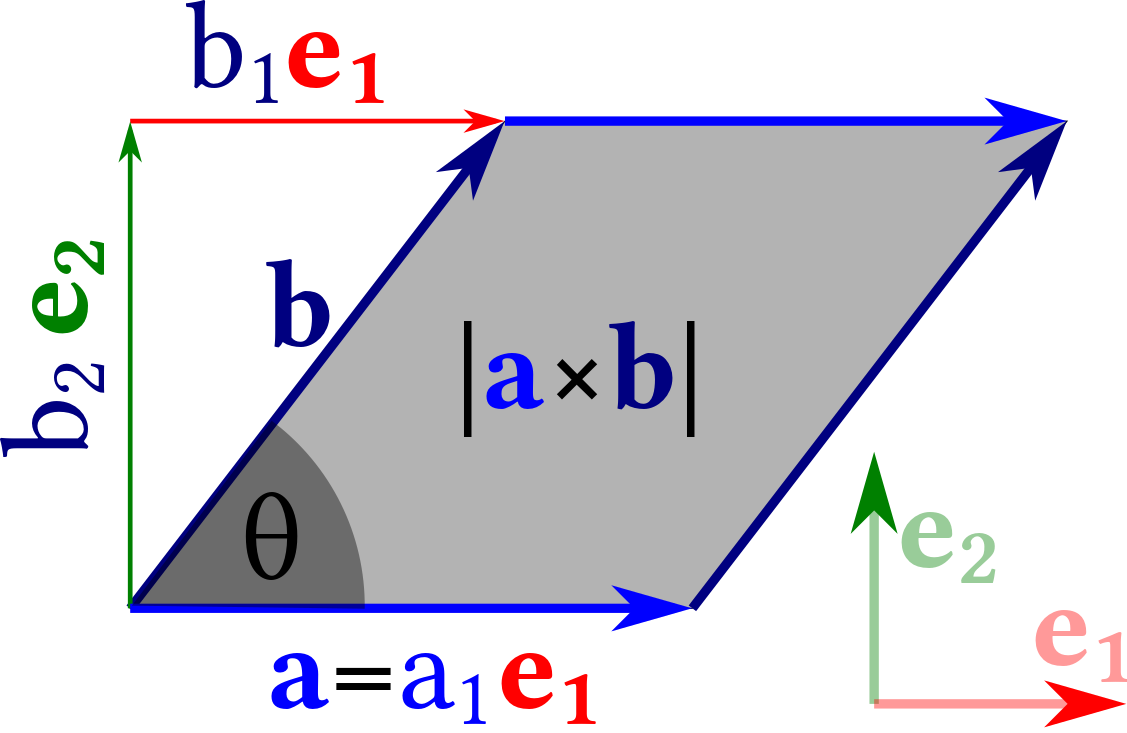
The cross product and the scalar triple product have distinct geometrical interpretations. The geometric meaning of the cross product $\mathbf a \times \mathbf b$ can best be seen by adopting a basis where the first basis vector is parallel to $\mathbf e_1 = \mathbf a / |\mathbf a|$, and the second basis vector $\mathbf e_2$ lies orthogonal to $\mathbf e_1$ in the plane spanned by $\mathbf a$ and $\mathbf b$. The third basis vector will then be $\mathbf e_3 = \mathbf e_1 \times \mathbf e_2$. The angle between $\mathbf a$ and$\mathbf b$, and hence also of $\mathbf e_1$ and$\mathbf b$ is denoted as$\theta$. Thus, $\mathbf b$ can be written as $\mathbf b = b_1 \, \mathbf e_1 + b_2 \, \mathbf e_2 = |\mathbf b| \, ( \cos\theta \, \mathbf e_1 + \sin\theta \, \mathbf e_2)$, cf.Figure 2.20. For this choice of the basis we find
\begin{align*} \mathbf a \times \mathbf b &= |\mathbf a| \, \mathbf e_1 \times ( b_1 \, \mathbf e_1 + b_2 \, \mathbf e_2 ) = |\mathbf a| \, b_1 \, \mathbf e_1 \times \mathbf e_1 + |\mathbf a| \, b_2 \, \mathbf e_1 \times \mathbf e_2 \\ &= |\mathbf a| \, |\mathbf b| \, \sin\theta \, \mathbf e_3 \end{align*}
Figure 2.20 illustrates that $|\mathbf a| \, |\mathbf b| \, \sin\theta$ amounts to the area of the parallelogram spanned by the vectors $\mathbf a$ and $\mathbf b$. Hence, the cross product amounts to a vector that is aligned vertically on the parallelogram, with a length that amounts to the area of the parallelogram.
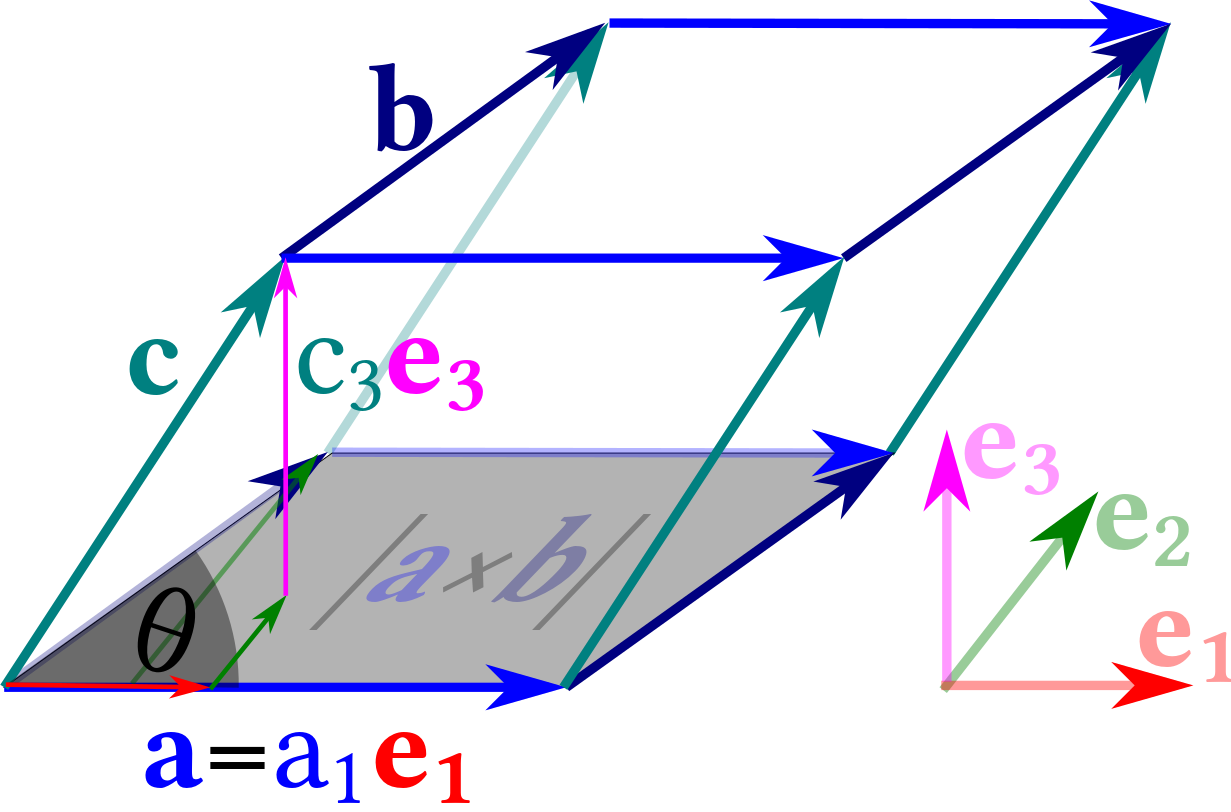
In order to evaluate also the product $( \mathbf a \times \mathbf b ) \cdot \mathbf c$ we introduce the coordinate representation of $\mathbf c$ as $\mathbf c = c_1 \, \mathbf e_1 + c_2 \, \mathbf e_2 + c_3 \, \mathbf e_3$ (Figure 2.21), and observe \begin{align*} ( \mathbf a \times \mathbf b ) \cdot \mathbf c &= |\mathbf a \times \mathbf b| \, \mathbf e_3 \cdot ( c_1 \, \mathbf e_1 + c_2 \, \mathbf e_2 + c_3 \, \mathbf e_3 ) \\ &= |\mathbf a \times \mathbf b| \, c_3 = a_1 \, b_2 \, c_3 \end{align*}
This amounts to the product of the area of the parallelogram spanned by $\mathbf a$ and $\mathbf b$
multiplied by the height of the parallelepiped spanned by the vectors $\mathbf a$, $\mathbf b$, $\mathbf c$.
Due to the special choice of the basis this volume amount to $a_1 \, b_2 \, c_3$
because all other contributions to the general expression $\sum_{ijk} a_i \, b_j \, c_k \, \varepsilon_{ijk}$ vanish.
The symmetry of the scalar triple product, property d) in Definition 2.14,
is understood from this perspective as the statement that the volume of the parallelepiped
is invariant under (cyclic) renaming of the vectors that define its edges.
As a final remark, we emphasize
that the geometric interpretation
that we have given to the cross product
holds in general — in spite of the special basis adopted in the derivation.
It is a distinguishing feature of vector spaces that the scalar numbers
that are derived from vectors take the same values every choice of the basis.
It is up to the physicist to find the basis that admits the easiest calculations.
2.9.3 The Torque
The cross product equips us with the mathematical notions to define the torque on a body.
Definition 2.15 Torque
The torque $\mathbf T$ defines a force
that is going to rotate a body around a position $\mathbf q_0$.
Let $\mathbf F_i$ be the forces that attach the body at the positions $\mathbf q_i$ with respect to the considered origin.
Then the torque is defined as
\begin{align*}
\mathbf T = \sum_i (\mathbf q_i - \mathbf q_0) \times \mathbf F_i
\end{align*}
Remark 2.32 The value of the torque depends on the choice of the reference position $\mathbf q_0$.
Remark 2.33 In general, the torques induced by different forces point in different directions. They are added as vectors. We will further discuss this below in Example 2.24.
Axiom 2.2 Torque balance
Let $N$ forces $\mathbf F_1, \dots, \mathbf F_N$ attack a body at the (body-fixed) positions $\mathbf q_i$.
The body does not rotate around the position $\mathbf q_0$ as long as the sum of the torques induced by the forces add to zero,
i.e. iff
\begin{align*}
\displaystyle \mathbf 0 = \mathbf T = \sum_{i=1}^N ( \mathbf q_i - \mathbf q_0) \times \mathbf F_i.
\end{align*}
Example 2.24 Sailing boat
When a sailboat is going broad reach, as shown in Figure 2.22, the following forces are acting on the boat:
- the wind in the sails generates a torque towards the bow around a horizontal axis that lies diagonal to the boat axis
- the buoyancy of the water generates a torque along a horizontal axis parallel to the boat the counteracts heeling
- the water drag on the hull generates a torque towards the bow around a horizontal axis that is orthogonal to the boat axis
- the fin and the rudder generate lift forces that generate a torque around a vertical axis
- the sailor stacks out in the trapeze to generate an additional torque in order to balance the torques
His aim is to minimize the heeling of the boat and to maximize the speed. The boat capsizes if he does not manage to balance the torques.
 Gwickecommonswiki, public domain
Gwickecommonswiki, public domain
Figure 2.22: A sailor stacking out in a trapeze in order to minimize the heeling of his sailboat.
2.9.4 Self Test
Problem 2.23:
Fill in the details of the proof for Remark 2.28.
Problem 2.24:
Fill in the details of the proof for Remark 2.30.
Problem 2.25: Turning a wheel
Two forces of magnitude $4\text{N}$ are acting on a wheel of radius $r$
that can freely rotate around its axis.
What magnitude should a third force, $\mathbf F$, have
that is attacking at a distance $r/2$ from the axis,
such that there is no net torque acting on the wheel?
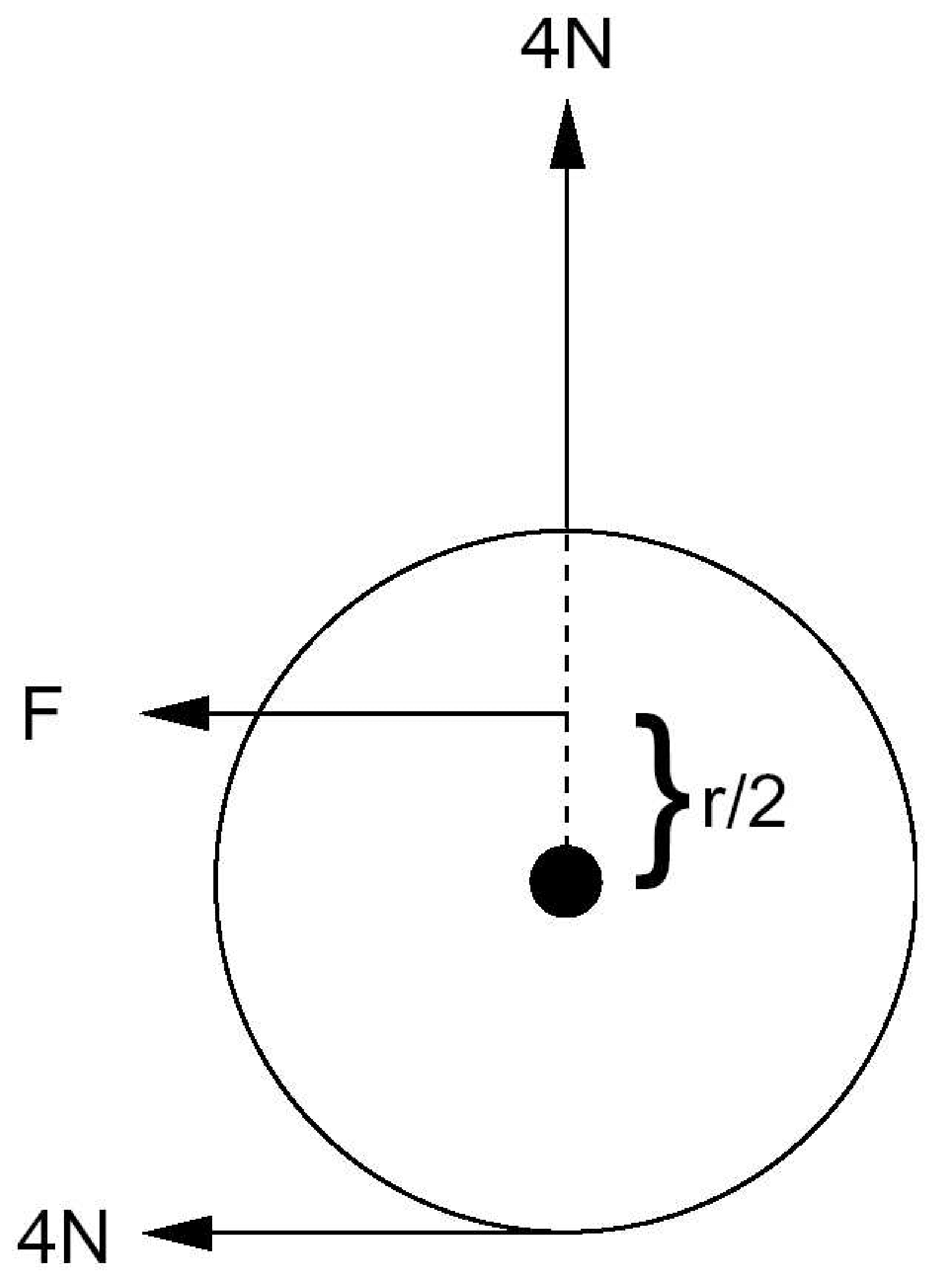 Figure 2.23: Setup for Problem 2.25.
Figure 2.23: Setup for Problem 2.25.
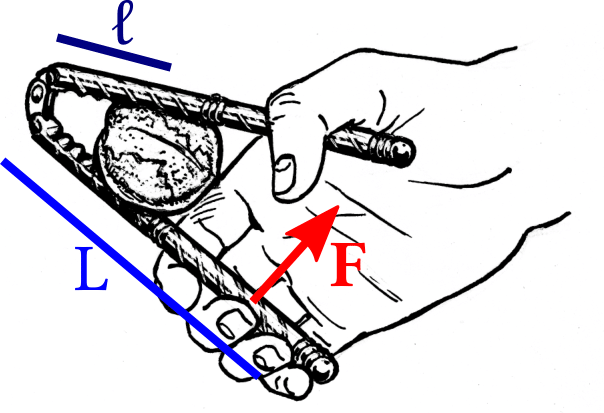 based on Pearson Scott Foresman nutcracker-tool, public domain
based on Pearson Scott Foresman nutcracker-tool, public domain
Figure 2.24: Setup for Problem 2.26.
Problem 2.26: Nutcrackers
A common type of nutcrackers employs the principle of lever arms
to crack nuts with a reasonable amount of force.
We idealize the nut as a spring with spring constant
$k = 1\text{kN/}mm$
and assume that it breaks
when it is compressed by $\Delta= 0.6mm$.
The nut is mounted at a distance of $l = 3cm$
from the joint of the nutcracker
and the hand exerts a force $\mathbf F$ at a distance $L$.
- Demonstrate that a force of magnitude $\displaystyle F = \frac{l k \Delta}{L}$ is required to crack the nut.
- Calculate the numerical value of $F$.
- If you try to crack the nut by placing it under a heavy stone: which mass should that stone have in order to crack the nut?