Die Philosophie steht in diesem großen Buch geschrieben,
dem Universum, das unserem Blick ständig offen liegt. Aber das Buch
ist nicht zu verstehen, wenn man nicht zuvor die Sprache erlernt und
sich mit den Buchstaben vetraut gemacht hat, in denen es geschrieben
ist. Es ist in der Sprache der Mathematik geschrieben, und deren
Buchstaben sind Kreise, Dreiecke und andere geometrische Figuren, ohne
die es dem Menschen unmöglich ist, ein einziges Wort davon zu
verstehen; ohne diese irrt man in einem dunklen Labyrinth herum.
Galileo Galilei — Il Saggiatore, 1623
Die Mathematik ist das Instrument, welches die Vermittlung bewirkt
zwischen Theorie und Praxis, zwischen Denken und Beobachten: sie baut
die verbindende Brücke und gestaltet sie immer tragfähiger. Daher
kommt es, daß unsere ganze gegenwärtige Kultur, soweit sie auf der
geistigen Durchdringung und Dienstbarmachung der Natur beruht, ihre
Grundlage in der Mathematik findet.
David Hilbert — Ansprache “Naturerkennen und Logik”
am 8.9.1930 während des Kongresses der Vereinigung deutscher Naturwissenschafter und Mediziner
Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen,
sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich
nicht auf die Wirklichkeit.
Albert Einstein — Festvortrag “Geometrie und Erfahrung”
am 27.1.1921 vor der Preußischen Akademie der Wissenschaften
Preface
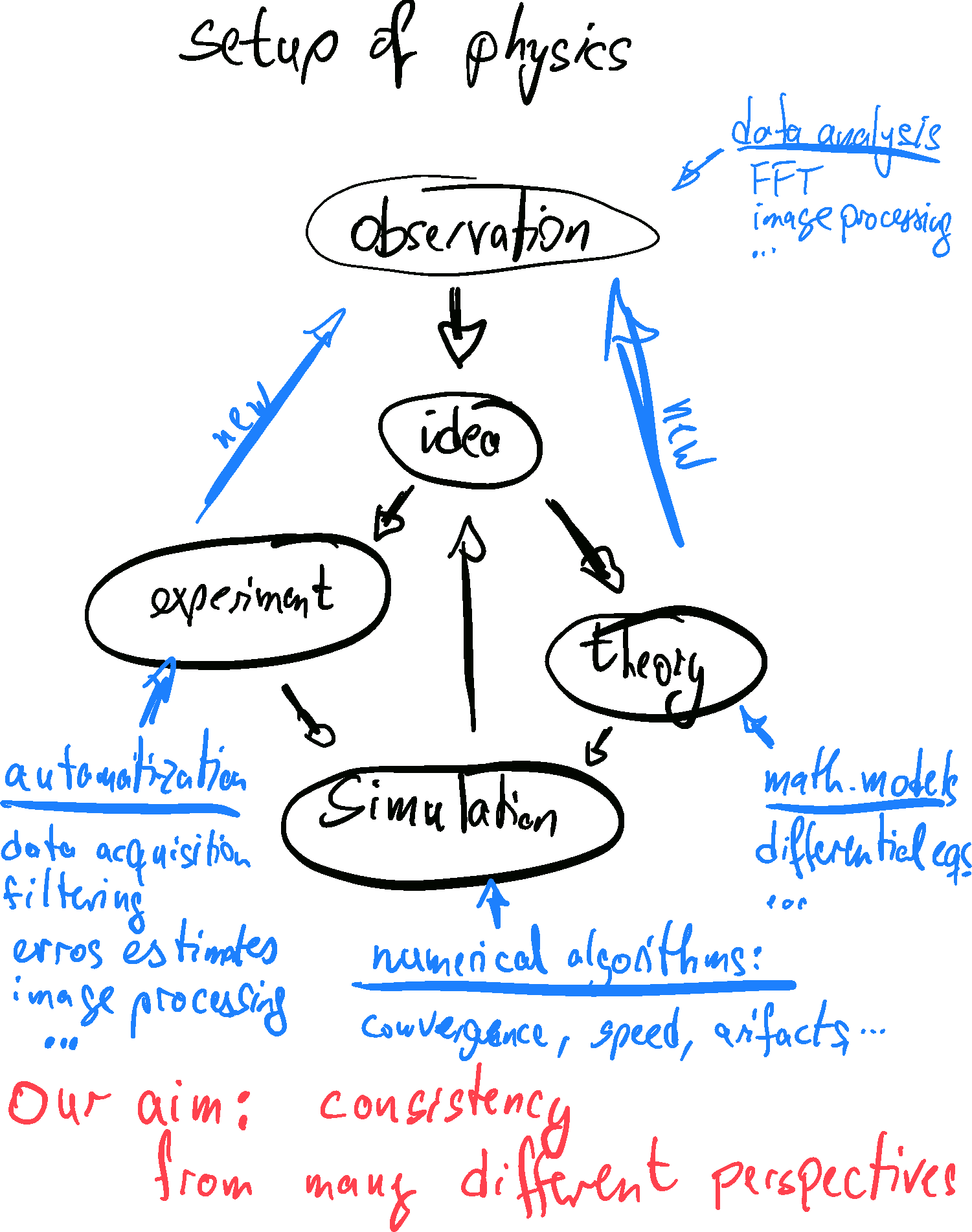
Almost 400 years ago Galilei Galileo expressed the credo of modern sciences: The language of mathematics is the appropriate instrument to decode the secrets of the universe. Arguably the fruits of this enterprise are more visible today than they have ever been in the past. Mathematical models are the cornerstone of modern science and engineering. They provide the tools for optimizing engines, and the technology for data and communication sciences. No car will run, no plane will fly, no cell phone ring without the technical equipment and the software to make it run. Moreover, again and again the challenges of physics models inspired the development of new mathematics. Physics and mathematics take complementary perspectives: Mathematicians strive for a logically stringent representation of the structure of theories and models. Physicists adopt mathematics as a tool to speak about and better understand nature:
The present Lecture Notes are developed to accompany courses on ``Theoretical Mechanics'' for physics freshmen in the international physics program and for students in the teacher education program of the Universität Leipzig. The course addresses mechanics problems to introduce the students to concepts and strategies aiming at a quantitative description of observations.
To meet that aim the lectures strive to meet several purposes:
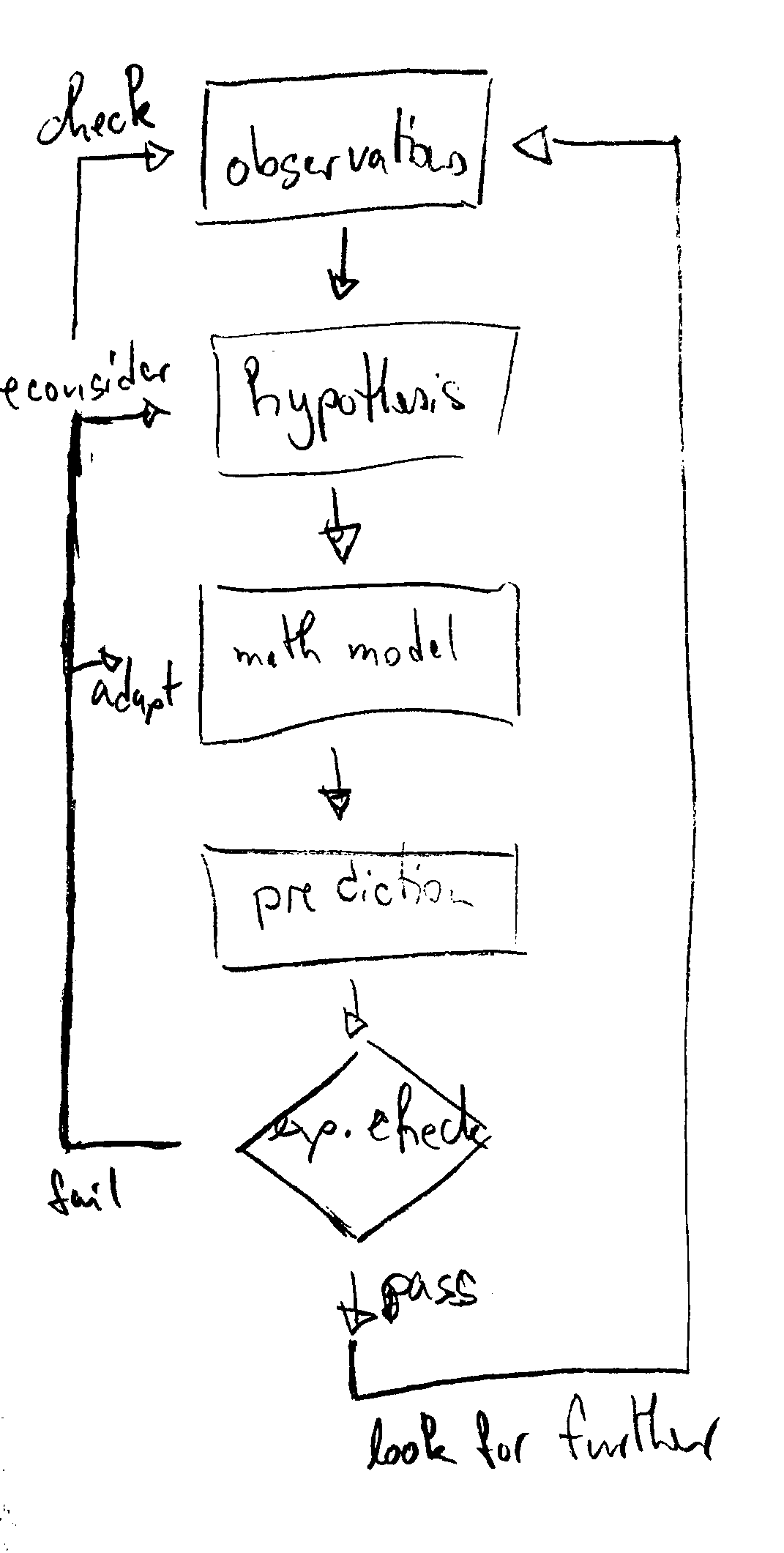
- They introduce the concept of a mathematical model, its predictions, and how they relate to observations.
- They present strategies adopted
- to develop a model,
- to explore its predictions,
- to falsify models, and
- to refine them based on comparison to observations.
- They introduce mathematical concepts used in this enterprise:
- dimensional analysis,
- non-dimensionalization,
- complex numbers,
- vector calculus, and
- ordinary differential equations.
- They provide an introduction to Newtonian and Lagrangian Mechanics.
Our approach to mathematical concepts is strongly biased to developing skills to apply mathematical tools in a modeling context, rather than striving for mathematical rigor. For the latter we point out potential pitfalls based on physical examples, and refer students to mathematics classes.
The material is organized in chapters that address subsequent mathematical and physical topics. Each chapter is introduced by a physics illustration problem. Then, we develop and discuss relevant new concepts. Subsequently, we provide a worked examples. One of them will be the solution of the problem sketched in the introduction. At the end of each section we provide problems:
- quickies to test conceptual understanding and highlight the new concepts. At times they involve a small twist or highlight pitfalls.
- exercises to gain practice in employing the concepts.
At the end of chapter further problems are given:
- more elaborate exercises where the new concepts are used to discuss non-trivial problems.
- exercises that provide complementary insight based on Python and Sage programs
- teasers with challenging problems. Typically these exercises require a non-trivial combination of different concepts that have been introduced in earlier chapters.
At the end of the chapter we recommend additional literature and provide an outlook for further reading. I am grateful to Robin Barta, Lennart Buchwald, Fabian Giese, Kolya Lettl, Menna Noufal, Annemarie Wenzel, and Maurice Zeuner for feedback on the notes. I am eager to receive further feedback. It is crucial for the development of this project to learn about typos, inconsistencies, confusing or incomplete explanations, and suggestions for additional material (contents as well as links to papers, books and internet resources) that should be added in forthcoming revisions. Everybody who is willing to provide feedback will be invited to a coffee in Café Corso.