Table of Contents
2. Balancing Forces and Torques
- 2.2 Sets
2.2 Sets
In mathematics and physics we often wish to make statements about a collection of objects, numbers, or other distinct entities.
Definition 2.1 Set
A set is a gathering of well-defined, distinct objects of our perception or thoughts.
An object $a$ that is part of a set $A$ is an element of $A$;
we write $a \in A$.
If a set $M$ has a finite number $n$ of elements we say that its cardinality is $n$.
We write $|M| = n$.
Remark. Notations and additional properties:
- When a set $M$ has a finite number of elements, e.g., $+1$ and $-1$, one can specify the elements by explicitly stating the elements, $M = \{ +1, -1 \}$. In which order they are states does not play a role, and it also does not make a difference when elements are provided several times. In other words the set $M$ of cardinality two can be specified by any of the following statements
\[ M = \{ -1, +1 \} = \{ +1, -1 \} = \{ -1, 1, 1, 1, \} = \{ -1, 1, +1, -1 \} \]
- If $e$ is not an element of a set $M$, we write $e \not\in M$. For instance $-1 \in M$ and $2 \not\in M$.
- There is exactly one set with no elements, i.e., with cardinality zero. It is denoted as empty set, $\emptyset$.
Example 2.2 Sets
- Set of capitals of German states:
$A_C = \{$Berlin, Bremen, Hamburg, Stuttgart, Mainz, Wiesbaden, München, Magdeburg, Saarbrücken, Potsdam, Kiel, Hannover, Dresden, Schwerin, Düsseldorf, Erfurt$\}$
- Set of small letters in German:
$A_L = \{$a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, ä, ö, ü, ß$\}$
- Set of month with $28$ days:1)
$A_M = \{$January, February, March, April, May, June, July, August, September, October, November, December$\}$
The cardinalities of these sets are
$|A_C| = 16$, $|A_L = 30|$, and $|A_M| = 12$.
Example 2.3 Sets of sets
A set can be an element of a set.
For instance the set
\[
M = \left\{ 1, \, 3, \, \left\{1, \, 2 \right\} \right\}
\]
has three elements
$1$, $3$ and $\left\{1, \, 2 \right\}$
such that
\(
|M| = 3
\),
and
\begin{align*}
1 &\in M \, , &
\left\{ 1, \, 2 \right\} \in M \, , \qquad
2 &\not\in M \, &
\left\{1\right\} &\notin M \, .
\end{align*}
Often it is bulky to list all elements of a set. In obvious cases we use ellipses such as $A_L = \{$a, b, c, \dots, z, ä, ö, ü, ß$\}$ for the set given in Example 2.2. Alternatively, one can provide a set $M$ by specifying the properties $A(x)$ of its elements $x$ in the following form \begin{align*} \underbrace{M}_{\text{The set } M} \underbrace{=}_{\text{contains}} \underbrace{\{}_{\text{all elements }} \underbrace{x}_{\text{$x$,}} \: \underbrace{:}_{\text{with :}} \: \underbrace{A(x)}_{\text{properties} \dots} \}. \end{align*} where the properties specify one of several properties of the elements. The properties are separated by commas, and must all be true for all elements of the set.
Example 2.4 Set definition by property
The set of digits $D = \left\{ 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9 \right\}$
can also be defined as follows
$D = \left\{ 1, \dots, 9 \right\} = \left\{ x : 0 < x \leq 9, x \in \mathbb{Z} \right\}$.
In the latter definition $\mathbb{Z}$ denotes the set of all integer numbers.
In order to specify the properties in a compact form we use logical junctors as short hand notation. In the present course we adopt the notations not $\lnot$, and $\land$, or $\lor$, implies $\Rightarrow$, and is equivalent $\Leftrightarrow$ for the relations indicated in Table 2.1.
| $A$ | $0$ | $0$ | $1$ | $1$ | |
|---|---|---|---|---|---|
| $B$ | $0$ | $1$ | $0$ | $1$ | |
| $ \lnot A $ | 1 | 1 | 0 | 0 | not $A$ |
| $ \lnot B $ | 1 | 0 | 1 | 0 | not $B$ |
| $ A \lor B $ | 0 | 1 | 1 | 1 | $A$ or $B$ |
| $ A \land B $ | 0 | 0 | 0 | 1 | $A$ and $B$ |
| $ A \Rightarrow B $ | 1 | 1 | 0 | 1 | $A$ implies $B$ |
| $ A \Leftrightarrow B $ | 1 | 0 | 0 | 1 | $A$ is equivalent to $B$ |
| $ A \lor \lnot B $ | 1 | 0 | 1 | 1 | $A$ or not $B$ |
| $ \lnot A \land B $ | 0 | 1 | 0 | 0 | not $A$ or $B$ |
| $ A \land \lnot B $ | 0 | 0 | 1 | 0 | $A$ and not $B$ |
Table 2.1: List of the results of different junctors acting on two statements $A$ and $B$. Here $0$ and $1$ indicate that a statement is wrong or right, respectively. In the rightmost column we state the contents of the expression in the left column in words. The final three lines provide examples of more complicated expressions.
The definition of the digits in Example 2.4 entails that all elements of $D$ are also numbers in $\mathbb{Z}$: we say that $D$ is a subset of $\mathbb{Z}$.
Definition 2.2 Subset and Superset
The set $M_1$ is a subset of $M_2,$
if all elements of $M_1$ are also contained in $M_2$.
We write2)
$M_1 \subseteq M_2$.
We denote $M_2$ then as superset of $M_1$,
writing $M_2 \supseteq M_1$.
The set $M_1$ is a proper subset of $M_2$ when at least one of the elements of $M_2$ is not contained in $M_1$.
In this case $|M_1| < |M_2|$,
and we write $M_1 \subset M_2$ or $M_2 \supset M_1$.
Example 2.5 Subsets
- The set of month with names that end with 'ber' is a subset of the set $A_M$ of Example 2.2:
\begin{align*} \{ \text{September, October, November, December} \} \subseteq A_M \end{align*}
- For the set $M$ of Example 2.3 one has
\begin{align*} \{ 1 \} \subseteq M \, , \quad \left\{ 1, \, 3 \right\} \subseteq M \, , \quad \left\{1, \, 2 \right\} \not\subseteq M \, , \quad \left\{ 2, \, \left\{1, \, 2 \right\} \right\} \not\subseteq M \, . \end{align*} Note that $\left\{1, \, 2 \right\}$ is an element of $M$. However, it is not a subset. The last two sets are no subsets because $2 \not\in M$.
Two sets are the same when they are subsets of each other.
Theorem 2.1 Equivalence of Sets
Two sets $A$ and $B$ are equal or equivalent, iff
\begin{align*}
(A \subseteq B) \; \land \; (B \subseteq A) \, .
\end{align*}
Remark. In mathematics “iff” indicates that something holds “if and only if”. Observe its use in the following two statements: A number is an even number if it is the product of two even numbers. A number is an even number iff it is the product of an even number and another number.
Remark. In logical expressions we first evaluate $\in$, $\not\in$ and other set operations that are used to build logical expressions. Then we evaluate the junctor $\lnot$ that is acting on a a single logical expression. Finally the other junctors $\land$, $\lor$, $\Rightarrow$, and $\Leftrightarrow$ are evaluated. Hence, the brackets are not required in Theorem 2.1.
Proof of Theorem 2.1
$A \subseteq B$ implies that $a \in A \Rightarrow a \in B$.
$B \subseteq A$ implies $b \in B \Rightarrow b \in A$.
If $A \subseteq B$ and $B \subseteq A$, then we also have $a \in A \Leftrightarrow a \in B$.
$\rule{3mm}{3mm}$
The description of sets by properties of its members, Example 2.4, suggests that one will often be interested in operations on sets. For instance the odd and even numbers are subsets of the natural numbers. Together they form this set, and one is left with the even numbers when removing the odd numbers from the natural numbers. Hence, we define the following operations on sets.
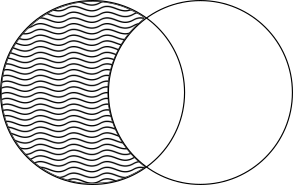
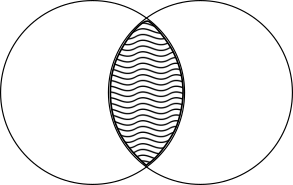Figure 2.2: Intersection of two sets.
$\quad$
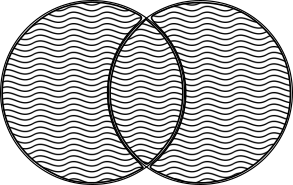Figure 2.3: Union of two sets.
$\quad$
Figure 2.4: Difference of two sets.
$\quad$
Figure 2.5: Complement of a set.
$\quad$
Definition 2.3 Set Operations
For two sets $M_1$ and $M_2$ we define the following operations:
- Intersection: $M_1 \bigcap M_2 = \left\{ m \; \vert \; m \in M_1 \land m \in M_2 \right\}$,
- Union: $M_1 \bigcup M_2 = \left\{ m \; \vert \; m \in M_1 \lor m \in M_2 \right\}$,
- Difference: $M_1 \backslash M_2 = \left\{ m \; \vert \; m \in M_1 \land m \notin M_2 \right\}$,
- The complement of a set $M$ in a universe $U$ is defined for subsets $M \subseteq U$ as $M^{C} = \left\{ m \in U \; \vert \; m \notin M \right\} = U \backslash M$.
- The Cartesian product of two sets $M_1$ and $M_2$ is defined as the set of ordered pairs $(a, \, b)$ of elements $a \in M_1$ and
$b \in M_2$: $\displaystyle M_1 \times M_2 = \left\{ (a, \, b) \; \vert \; a \in M_1, \, b \in M_2 \right\} $.
A graphical illustration of the operations is provided in Figure 2.2, Figure 2.3, Figure 2.4, Figure 2.5.
Example 2.6 Set operations: participants in my class
Consider the set of participants $P$ in my class.
The sets of female $F$ and male $M$ participants of the class are proper subsets of $P$ with an empty intersection $F \bigcap M$.
The set of non-female participants is $P \backslash F$.
The set of heterosexual couples in the class is a subset of the Cartesian product $F \times M$.
Furthermore, the union $F \bigcup M$ is a proper subset of $P$, when there is a participant who is neither female nor male.
Definition 2.4 Logical quantors
A logical statements $\mathsf S$ about elements $a$ of a set $A$ may hold
- for all elements of a set — we write: $\forall a \in A \; \vert \; \mathsf S$
- for some elements of a set — we write: $\exists a \in A \; \vert \; \mathsf S$
- for exactly one elements of a set — we write: $\exists! a \in A \; \vert \; \mathsf S$
Example 2.7 Logical quantors and properties of set elements
Let $|m|$ denote the number of days in a month $a \in A_M$ (Refer to Example 2.2).
Then the following statements are true:
There is exactly one month that has exactly $28$ days:
\begin{align*}
\exists! a \in A_M \; \vert \; |a| = 28
\end{align*}
Some months have exactly $30$ days:
\begin{align*}
\exists a \in A_M \; \vert \; |a| = 30
\end{align*}
All month have at least $28$ days:
\begin{align*}
\forall a \in A_M \; \vert \; |a| \geq 28
\end{align*}
2.2.1 Sets of Numbers
Many sets of numbers that are of interest in physics have infinitely many elements. We construct them in Table 2.2 based on the natural numbers \begin{align*} \mathbb N = \left\{1, \, 2, \, 3, \, \ldots \right\} \end{align*} or the natural numbers with zero \begin{align*} \mathbb N_0 = \mathbb N \bigcup \left\{ 0 \right\} \, . \end{align*} Remark. Some authors adopt the convention that zero is included in the natural numbers $\mathbb N$. When this matters you have to check which convention is adopted.
There are many more sets of numbers. For instance, in mathematics the set of constructable numbers is relevant for certain proofs in geometry, and in physics and computer graphics quaternions are handy when it comes to problems involving three-dimensional rotations. In any case one needs intervals of numbers.
| name | symbol | description |
|---|---|---|
| natural numbers | $\mathbb{N}$ | $\left\{ 1, \, 2, \, 3, \, \ldots \right\}$ |
| natural numbers with $0$ | $\mathbb{N}_0$ | $\mathbb{N} \bigcup \left\{ 0 \right\}$ |
| negative numbers | $-\mathbb{N}$ | $\left\{ -n \; \vert \; n \in \mathbb{N} \right\}$ |
| even numbers | $2 \mathbb{N}$ | $\left\{ 2\,n \; \vert \; n \in \mathbb{N} \right\}$ |
| odd numbers | $2 \mathbb{N} - 1$ | $\left\{ 2\,n -1 \; \vert \; n \in \mathbb{N}\right\}$ |
| integer numbers | $\mathbb{Z}$ | $\left( -\mathbb{N} \right) \bigcup \mathbb{N}_0$ |
| rational numbers | $\mathbb{Q}$ | $\left\{ \frac{p}{q} \; \vert \; p \in \mathbb{Z}, \, q \in \mathbb{N} \right\}$ |
| real numbers | $\mathbb{R}$ | see below |
| complex numbers | $\mathbb{C}$ | $\mathbb{R}+ \text{i}\mathbb{R},$ where $\text{i} = \sqrt{-1}$ |
Table 2.2: Summary of important sets of numbers.
Definition 2.5 Interval of Real Numbers $\mathbb{R}$ An interval is a continuous subset of a set of numbers. We distinguish open, closed, and half-open subsets.
- closed interval: $[a, \, b] = \left\{ x \; \vert \; x \geq a, \, x \leq b \right\},$
- open interval: $(a, \, b) = \; ]a, \, b[ \; = \left\{ x \; \vert \; x > a, \, x < b \right\},$
- right open interval: $[a, \, b) = [a, \, b[ \; = \left\{ x \; \vert \; x \geq a, \, x < b \right\},$
- left open interval: $(a, \, b] \; = \; ]a, \, b] = \left\{ x \; \vert \; x > a, \, x \leq b \right\}.$
Subsets of $\mathbb{R}$ will be denoted as real intervals.
2.2.2 Self Test
Problem 2.1: Relations between sets
Let $A$, $B$, $C$, and $D$ be pairwise distinct elements. Select one of the symbols \begin{align*} \qquad\qquad \in,\quad \not\in,\quad \ni,\quad \not\ni,\quad \subset,\quad \not\subset,\quad \supset,\quad \not\supset,\quad = \\ \end{align*} and avoid $\not\in, \; \not\ni, \; \not\subset, \; \not\supset$ wherever possible.
- a) $\quad\lbrace A, B \rbrace \quad {{ \Box}} \quad \lbrace A, B, C \rbrace$,
- c) $\quad\lbrace \emptyset \rbrace \quad {\Box} \quad \emptyset$,
- e) $\quad A \quad { \Box} \quad \lbrace A, B, C \rbrace$,
- g) $\quad\lbrace A, C, D \rbrace \setminus \lbrace A, B \rbrace \;\Box\; \lbrace A, B, C \rbrace$,
- b) $\lbrace A \rbrace \quad { \Box} \quad B$,
- d) $\lbrace \lbrace A \rbrace \rbrace \quad { \Box} \lbrace \lbrace A \rbrace, \lbrace B \rbrace \rbrace$,
- f) $\lbrace A, C, D \rbrace \cap \lbrace A, B \rbrace \, {\Box} \, \lbrace A, B, C, D \rbrace$,
- h) $\lbrace A, C, D \rbrace \cup \lbrace A, B \rbrace \quad { \Box} \quad A$.
Problem 2.2: Intervals
- Provide $\lbrack 1; 17 \rbrack \cap \rbrack 0; 5 \lbrack$ as a single interval.
- Provide $[-1, 4] \backslash [1, 2[$ as union of two intervals.
Problem 2.3: Sets of numbers
Which of the following statements are true?
- $\lbrace 6 \cdot z \vert z \in \mathbb{Z} \rbrace \subset \lbrace 2 \cdot z \vert z \in \mathbb{Z} \rbrace$.
- $\left\lbrace 2 \cdot z \vert z \in \mathbb{Z} \right\rbrace \cap \left\lbrace 3 \cdot z \vert z \in \mathbb{Z} \right\rbrace = \left\lbrace 6 \cdot z \vert z \in \mathbb{Z} \right\rbrace$.
- Let $T(a)$ be the set of numbers that divide $a$. Then $\quad\displaystyle \forall a, b \in \mathbb{N} \; \vert \; T(a) \cup T(b) = T(a \cdot b) $.
Example: $T(2) = \{1,2\}$, $T(3) = \{1,3\}$, and $T(6) = \{1,2,3,6\}$.