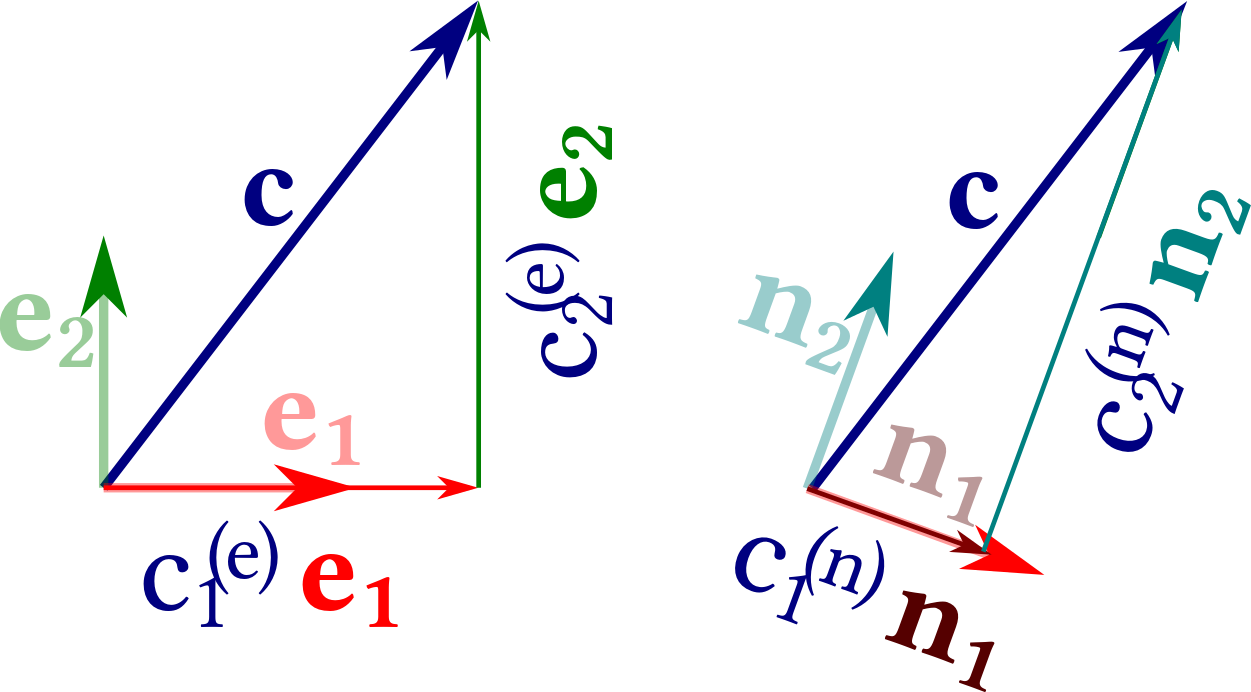2. Balancing Forces and Torques
- 2.8 Cartesian coordinates
2.8 Cartesian coordinates
Theorem 2.2 entails an extremely elegant possibility to deal with vectors. We first illustrate the idea based on a two-dimensional example, Figure 2.14, and then we develop the general theory:
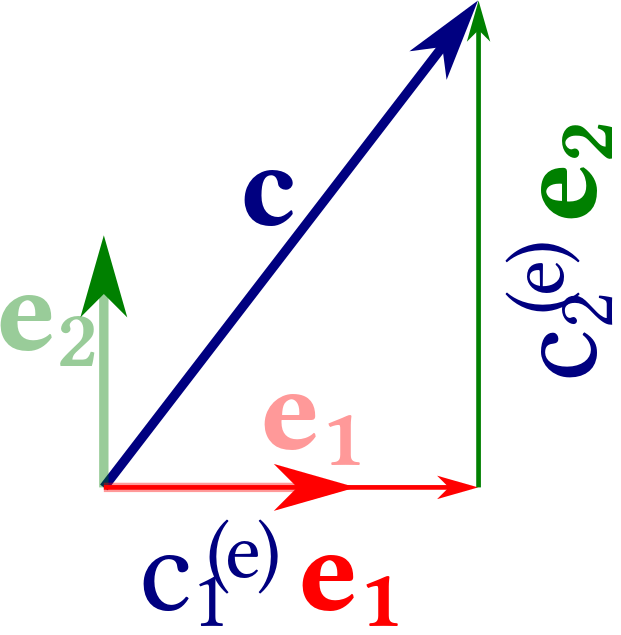
Figure 2.14: Representation of the vector $\mathbf c$ in terms of the orthogonal unit vectors $(\mathbf e_1, \mathbf e_2)$.
Let $\mathbf e_1$ and $\mathbf e_2$ be two orthogonal vectors that have unit length, \begin{align*} \langle \mathbf e_1| \mathbf e_1 \rangle = \langle \mathbf e_2 \mid \mathbf e_2 \rangle = 1 \quad\text{and}\quad \langle \mathbf e_1| \mathbf e_2 \rangle = 0 \end{align*} For every vector $\mathbf c$ in the plane described by these two vectors, we can then find two numbers $c_1^{(e)}$ and $c_2^{(e)}$ such that \begin{align*} \mathbf c = c_1^{(e)} \: \mathbf e_1 + c_2^{(e)} \: \mathbf e_2 \end{align*} Now the choice of the vectors $(\mathbf e_1, \mathbf e_2)$ entails that triangle with edge $\mathbf c$, $c_1^{(e)} \: \mathbf e_1$, and $c_2^{(e)} \: \mathbf e_2$ is right-angled and that \begin{align*} c_i^{(e)} &= |\mathbf c| \; \cos\angle(\mathbf c, \mathbf e_i) = \langle \mathbf c \mid \mathbf e_i \rangle \quad\text{for \ } i \in \{ 1, 2 \} \\ \Rightarrow\quad \mathbf c &= \langle \mathbf c \mid \mathbf e_1 \rangle \; \mathbf e_1 + \langle \mathbf c \mid \mathbf e_2 \rangle \; \mathbf e_2 \end{align*} This strategy to represent vectors applies in all dimensions.
Definition 2.13 Basis and Coordinates
Let $\mathsf{B} = \{ \mathbf e_i, \; i \in \{1, \dots, D \}$ be a set of $D$ pairwise orthogonal unit vectors
\begin{align*}
\forall i,j \in \{1, \dots, D \} : \quad
\mathbf e_i \cdot \mathbf e_j
=\left\{ \begin{array}{ll}
1 & \text{ if } i=j \\
0 & \text{ else }
\end{array}
\right.
\end{align*}
in a vector space $(\mathsf{V}, \mathbb{F}, +, \cdot)$ with inner product $\langle\_|\_\rangle$.
We say that $\mathsf{B}$ forms a basis for a $D$-dimensional vector space iff
\begin{align*}
\forall \mathbf v \in \mathsf{V}\; \exists v_i, \: i \in \{1, \dots, D \} : \quad
\mathbf v = \sum_{i=1}^D v_i^{(e)} \; \mathbf e_i
\end{align*}
In that case we also have $v_i^{(e)} = \langle \mathbf v \, | \, \mathbf e_i \rangle$, $i \in \{1, \dots, D \}$
and these numbers are called the coordinates of the vector $\mathbf v$.
The number of vectors $D$ in the basis of the vector space is denoted as
dimension of the vector space.
Representation of the vector $\mathbf c$ of Figure 2.14 in terms of the bases $(\mathbf e_1, \mathbf e_2)$ and $(\mathbf n_1, \mathbf n_2)$.
Remark 2.21 The choice of a basis, and hence also of the coordinates, is not unique. Figure 2.15 shows the representation of a vector in terms of two different bases $(\mathbf e_1, \mathbf e_2)$ and $(\mathbf n_1, \mathbf n_2)$. We suppress the superscript that indicates the basis when the choice of the basis is clear from the context.
Remark 2.22 For a given basis the representation in terms of coordinates is unique.
Proof. 1. The coordinates $a_i$ of a vector $\mathbf a$ are explicitly given by $a_i = \langle a \mid \mathbf e_i\rangle$. This provides unique numbers for a given basis set.
2. Assume now that two vectors $\mathbf a$ and $\mathbf b$ have the same coordinate representation. Then the vector-space properties imply \begin{align*} \left.\begin{array}{l} \mathbf a = \sum_i c_i \, \mathbf e_i\\ \mathbf b = \sum_i c_i \, \mathbf e_i \end{array}\right\} &\Rightarrow \begin{aligned}[t] \mathbf a - \mathbf b &= \left( \sum_i c_i \: \mathbf e_i \right) - \left( \sum_i c_i \: \mathbf e_i \right) \\ &= \sum_i (c_i - c_i) \, \mathbf e_i = \sum_i 0 \, \mathbf e_i = \mathbf 0 \end{aligned} \\ &\Rightarrow \quad \mathbf a = \mathbf b \end{align*} Hence, they must be identical.
Remark 2.23 (Kronecker $\delta_{ij}$)
It is convenient to introduce the abbreviation $\delta_{ij}$ for
\begin{align*}
\delta_{ij} = \left\{ \begin{array}{ll}
1 & \text{if } i=j,
& 0 & \text{else}
\end{array}
\right.
\end{align*}
where $i,j$ are elements of some index set. This symbol is denoted as Kronecker $\delta$. With the Kronecker symbol the condition on orthogonal unit vectors of a basis can more concisely be written as
\begin{align*}
\mathbf e_i \cdot \mathbf e_j = \delta_{ij}
\end{align*}
Moreover, for $i,j \in \{1, \dots, D\}$ the numbers, $\delta_{ij}$,
describe a $D\times D$ matrix which is the neutral element for multiplication
with another $D\times D$ matrix, and also with a vector of $\mathbb{R}^D$, when it is interpreted as a $D \times 1$ matrix.
Theorem 2.3 Scalar product on $\mathbb{R}^D$ and $\mathbb{C}^D$ The axioms of vector spaces and the inner product imply that \begin{align*} \text{on } \mathbb{R}^D : \qquad \langle \mathbf a \mid \mathbf b \rangle =& \sum_{i=1}^D \langle \mathbf a \mid i \rangle \, \langle i \mid \mathbf b \rangle = \sum_{i=1}^D a_i b_i \\ \text{on } \mathbb{C}^D : \qquad \langle \mathbf a \mid \mathbf b \rangle =& \sum_{i=1}^D \langle \mathbf a \mid i \rangle \, \langle i \mid \mathbf b \rangle = \sum_{i=1}^D a_i \bar b_i \end{align*} where the bar indicates complex conjugation of complex numbers. This can be written as follows when representing the coordinates as a 1D array of numbers \begin{align*} \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_D \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_D \end{pmatrix} = a_1 \, \bar b_1 + a_2 \, \bar b_2 + \cdots + a_D \, \bar b_D \end{align*} where the complex conjugation does not apply for real numbers. This latter form of the inner product is denoted as scalar product.
Proof. We first note that the case of real numbers can be interpreted as special case of the complex numbers with a vanishing complex part. Hence, we only provide the proof for the complex case. We use the representations $\mathbf a = \sum_i \langle \mathbf a \mid \mathbf e_i \rangle \, \mathbf e_i$ and $\mathbf b = \sum_j \langle \mathbf b \mid \mathbf e_j \rangle \, \mathbf e_j$, and work step by step from the left to the aspired result: \begin{align*} \langle \mathbf a \mid \mathbf b \rangle &= \Biggl\langle \sum_i \, \langle \mathbf a \mid \mathbf e_i \rangle \, \mathbf e_i \Biggm| \sum_j \, \langle \mathbf b \mid \mathbf e_j \rangle \, \mathbf e_j \Biggr\rangle \\ &= \sum_i \, \langle \mathbf a \mid \mathbf e_i \rangle \, \Biggl\langle \mathbf e_i \Biggm| \sum_j \langle \mathbf b \mid \mathbf e_j \rangle \, \mathbf e_j \Biggr\rangle \\ &= \sum_i \, \langle \mathbf a \mid \mathbf e_i \rangle \; \sum_j \, \overline{ \langle \mathbf b \mid \mathbf e_j \rangle } \: \langle \mathbf e_i \mid \mathbf e_j \rangle \\ &= \sum_i \, \langle \mathbf a \mid \mathbf e_i \rangle \; \sum_j \, \langle \mathbf e_j \mid \mathbf b \rangle \: \delta_{ij} \\ &= \sum_i \, \langle \mathbf a \mid \mathbf e_i \rangle \; \langle \mathbf e_i \mid \mathbf b \rangle \, . \end{align*} Due to $a_i = \langle \mathbf a \mid \mathbf e_i \rangle$ and $\bar b_i = \langle \mathbf e_i \mid \mathbf b \rangle$ we therefore have \begin{align*} \langle \mathbf a \mid \mathbf b \rangle = \sum_i a_i \: \bar b_i \\ \end{align*}
Remark 2.24
Einstein pointed out that the sums over pairs of identical indices
arise ubiquitously in calculations like to proof of Theorem 2.3.
He therefore adopted the convention that one always sums over pairs of identical indices,
and does no longer explicitly write that down.
This leads to substantially clearer representation of the calculation.
For instance, the proof looks then as follows:
\begin{align*}
\langle \mathbf a \mid \mathbf b \rangle
&= \Bigl\langle
\langle \mathbf a \mid \mathbf e_i \rangle \, \mathbf e_i \Bigm|
\langle \mathbf b \mid \mathbf e_j \rangle \, \mathbf e_j \Bigr\rangle
= \langle \mathbf a \mid \mathbf e_i \rangle \,
\Bigl\langle \mathbf e_i \Bigm|
\langle \mathbf b \mid \mathbf e_j \rangle \, \mathbf e_j \Bigr\rangle
\end{align*}
\begin{align*}
&= \langle \mathbf a \mid \mathbf e_i \rangle \;
\overline{ \langle \mathbf b \mid \mathbf e_j \rangle } \: \langle \mathbf e_i \mid \mathbf e_j \rangle
= \langle \mathbf a \mid \mathbf e_i \rangle \;
\overline{ \langle \mathbf b \mid \mathbf e_j \rangle } \:
\delta_{ij}
\end{align*}
\begin{align*}
&= \langle \mathbf a \mid \mathbf e_i \rangle \;
\langle \mathbf e_i \mid \mathbf b \rangle
\end{align*}
\begin{align*}
\Rightarrow\quad
\langle \mathbf a \mid \mathbf b \rangle &= a_i \; \bar b_i
\end{align*}
Remark 2.25 Dirac pointed out that the vector product $\langle \mathbf a \mid \mathbf b \rangle$ takes the form of the multiplication of a $1\times D$ matrix for $\mathbf a$ and a $D \times 1$ matrix for $\mathbf b$. He suggested to symbolically write down these vectors as a bra vector $\langle a|$ and a ket vector $| b \rangle$. When put together as a bra-( c)-ket $\langle a| b \rangle$ one recovers the inner product, and introducing $|\mathbf e_i \rangle\langle e_i|$ and observing Einstein notation comes down to inserting a unit matrix. For instance for $2\times 2$ vectors \begin{align*} \langle \mathbf a \mid \mathbf b \rangle = (a_1, a_2) { \bar b_1 \choose \bar b_2 } = (a_1, a_2) { \: 1 \quad 0 \: \choose \: 0 \quad 1 \:} { \bar b_1 \choose \bar b_2 } = \langle \mathbf a \mid \mathbf e_i \rangle \langle \mathbf e_i \mid \mathbf b \rangle \end{align*} Conceptually this is a very useful observation because it provides an easy rule to sort out what changes in the equations when one represents a problem in terms of a different basis.
Example 2.22 Changing coordinates from basis $(\mathbf e_i)$ to basis $(\mathbf n_i)$
We observe Dirac's observation that the expressions $| e_i\rangle\langle e_i|$
and $| n_i\rangle\langle n_i|$ sandwiched between a bra and a ket amounts to multiplication with one.
Hence, the coordinates change according to
\begin{align*}
a_i^{(n)}
= \langle \mathbf a \mid \mathbf n_i\rangle
= \langle \mathbf a \mid \mathbf e_j \rangle \langle \mathbf e_j| \mathbf n_i\rangle
= a_j^{(e)} \langle \mathbf e_j| \mathbf n_i\rangle
\end{align*}
which amounts to multiplying the vector with entries $( a_j^{(e)} , j=1,\dots, D )$ with the $D \times D$ matrix $T$ with entries $t_{ji} = \langle \mathbf e_j| \mathbf n_i\rangle$.
On the other hand, for the inner products we have
\begin{align*}
a_i^{(e)} \bar b_i^{(e)}
&= \langle \mathbf a \mid \mathbf b \rangle
= \langle \mathbf a \mid \mathbf e_i \rangle \langle \mathbf e_i \mid \mathbf b \rangle
\\
&= \langle \mathbf a \mid \mathbf n_j \rangle \langle \mathbf n_j \mid \mathbf e_i \rangle \langle \mathbf e_i \mid \mathbf n_k \rangle \langle \mathbf n_k |\mathbf b \rangle
= \langle \mathbf a \mid \mathbf n_j \rangle \langle \mathbf n_j \mid \mathbf n_k \rangle \langle \mathbf n_k |\mathbf b \rangle
\\
&= \langle \mathbf a \mid \mathbf n_j \rangle \: \delta_{jk} \: \langle \mathbf n_k |\mathbf b \rangle
= \langle \mathbf a \mid \mathbf n_j \rangle \langle \mathbf n_j |\mathbf b \rangle
= a_i^{(n)} \bar b_i^{(n)}
\end{align*}
Its value does not change,
even though the coordinates take entirely different values.
2.8.1 Self Test
Problem 2.19: Cartesian coordinates in the plane
a) Mark the following points in a Cartesian coordinate system: \begin{align*} (0, \, 0) \quad (0, \, 3) \quad (2, \, 5) \quad (4, \, 3) \quad (4, \,0) \end{align*} Add the points $(0, \, 0) \; (4, \, 3) \; (0, \, 3) \; (4, \, 0)$, and connect the points in the given order. What do you see?
b) What do you find when drawing a line segment connecting the following points? \begin{align*} (0, \, 0) \quad (1, \, 4) \quad (2, \, 0) \quad (-1, \, 3) \quad (3, \, 3) \quad (0, \, 0) \end{align*}
Problem 2.20: Geometric and algebraic form of the scalar product
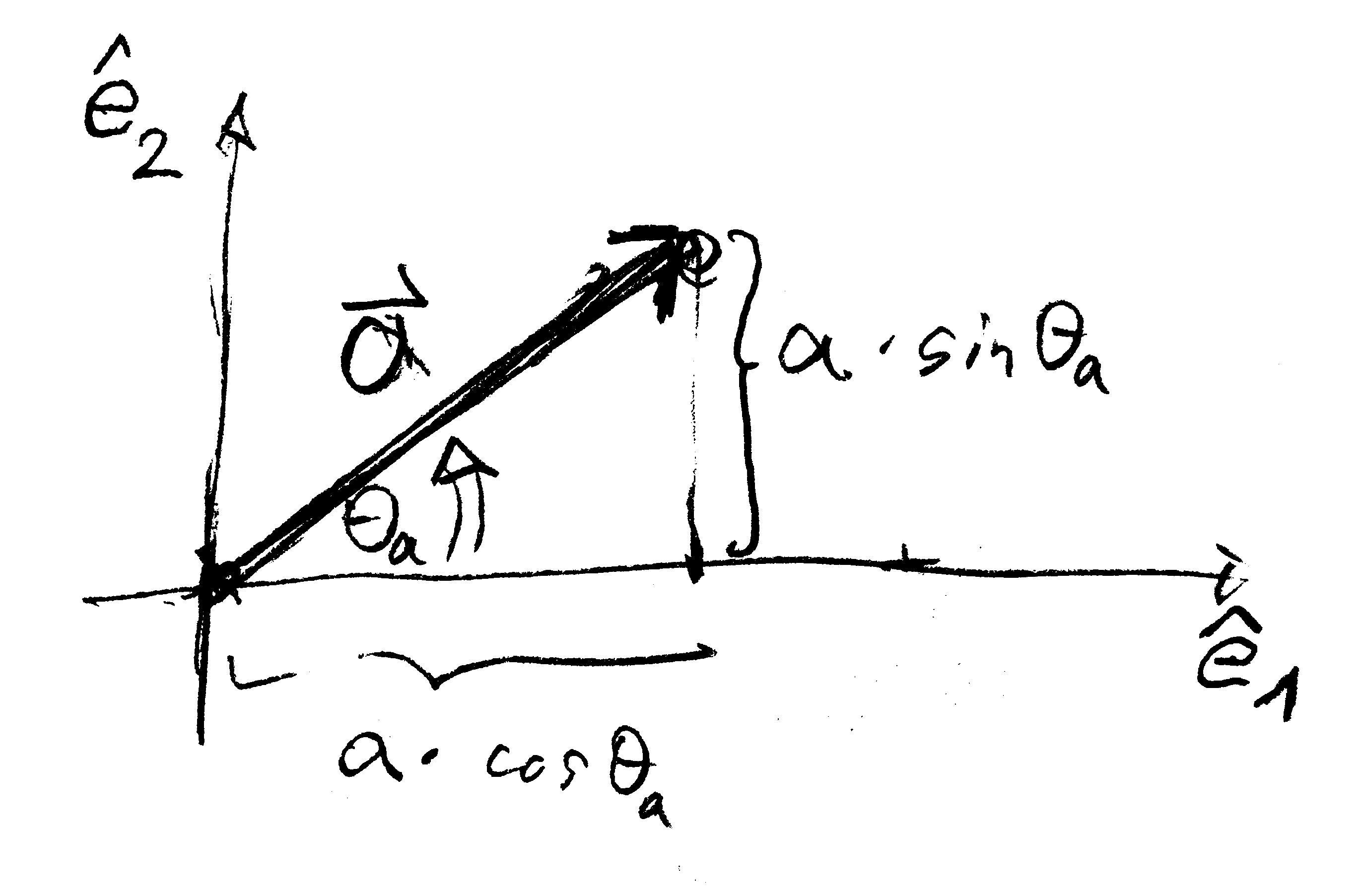
The sketch in the margin shows a vector $\mathbf a$ in the plane, and its representation as a linear combination of two orthonormal vectors $(\hat{\boldsymbol e}_1, \hat{\boldsymbol e}_2)$, \begin{align*} \mathbf a = a \, \cos\theta_a \: \hat{\boldsymbol e}_1 + a \, \sin\theta_a \: \hat{\boldsymbol e}_2 \end{align*} Here, $a$ is the length of the vector $\mathbf a$, and $\theta_1 = \angle(\hat{\boldsymbol e}_1, \mathbf a)$.
a) Analogously to $\mathbf a$ we consider another vector $\mathbf b$ with a representation \begin{align*} \mathbf b = b \, \cos\theta_b \: \hat{\boldsymbol e}_1 + b \, \sin\theta_b \: \hat{\boldsymbol e}_2 \end{align*} Employ the rules of scalar products, vector addition and multiplication with scalars to show that \begin{align*} \mathbf a \cdot \mathbf b = a \, b \: \cos(\theta_a -\theta_b) \end{align*} Hint:
b) As a shortcut to the explicit calculation of a) one can introduce the coordinates $a_1 = a \, \cos\theta_a$ and $a_2 = a \, \sin\theta_a$, and write $\mathbf a$ as a tuple of two numbers. Proceeding analogously for $\mathbf b$ one obtains \[ \mathbf a = \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \qquad \mathbf b = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \] How does the product $\mathbf a \cdot \mathbf b$ look like in terms of these coordinates?
c) How do the arguments in a) and b) change for $D$ dimensional vectors that are represented as linear combinations of a set of orthonormal basis vectors $\hat{\boldsymbol e}_1, \dots, \hat{\boldsymbol e}_D$?

Problem 2.21:
Scalar product on $\mathbb{R}^D$
Show that the scalar product on $\mathbb{R}^D$ takes exactly the same form as for the complex case, Theorem 2.3. However, complex conjugation is not necessary in that case.
Problem 2.22:
Pauli matrices form a basis for a 4D vector space
Show that the Pauli matrices
\begin{align*}
\sigma_0 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \, ,
\quad
\sigma_1 = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \, ,
\quad
\sigma_2 = \begin{pmatrix} 0 & -\mathrm{i} \\ \mathrm{i} & 0 \end{pmatrix} \, ,
\quad
\sigma_3 = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
\end{align*}
form a basis of the real vector space of $2 \times 2$ Hermitian matrices, $\mathbb{H}$, with
\begin{align*}
A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \in \mathbb{H}
\quad \Leftrightarrow \quad
a_{ij} \in \mathbb{C} \; \land \; a_{ij}=a_{ji}^*
\end{align*}
Show to that end:
a) The matrices $\sigma_0$, $\dots$, $\sigma_4$ are linearly independent.
b) $\displaystyle x_0, \dots, x_4 \in \mathbb{R} \quad\Rightarrow\quad \sum_{i=0}^4 x_i \, \sigma_i \in \mathbb{H}$
c) $\displaystyle M \in \mathbb{H} \quad\Rightarrow \quad \exists x_0, \dots, x_4 \in \mathbb{R} : M = \sum_{i=0}^4 x_i \, \sigma_i$