2. Balancing Forces and Torques
- 2.4 Fields
2.4 Fields
Besides being of importance to characterize the action of symmetry operations like reflections or rotations, groups are also important for us because they admit further characterization of sets of numbers. The natural numbers are not a group. For the addition they are lacking the neutral elements, and for adding and multiplications they are lacking inverse elements. In contrast the group $\left( \mathbb{Z}, \, + \right)$ is a commutative group with infinitely many elements.
Example 2.11 The group $\left( \mathbb{Z}, \, + \right)$
The numbers $\mathbb{Z}$ with operation $+$ form a group.
This is demonstrated here by checking the group axioms.
- a) Addition of any two numbers provides a number:
$\forall x,y \in \mathbb{Z} : (x+y) \in \mathbb{Z} $.
- b) The neutral element of the addition is $0$:
$\exists \: 0 \in \mathbb{Z} \; \forall z \in \mathbb{Z} : z + 0 = z = 0 + z$.
- c) For every element $z \in \mathbb{Z}$ there is an inverse $(-z) \in \mathbb{Z}$:
$\forall z \in \mathbb{Z} \; \exists (-z) \in \mathbb{Z} : z + (-z) = 0 = (-z) + z$.
- d) The addition of numbers is associative:
$\forall z_1, \, z_2, \, z_3 \in \mathbb{Z} : z_1 + (z_2 + z_3) = (z_1 + z_2) + z_3$.
However, the numbers $\mathbb{Z}$ still lack inverse elements of the multiplication. The rational numbers $\mathbb{Q}$ and the real numbers $\mathbb{R}$ are commutative groups for addition and multiplication (with the special rule that multiplication with $0$ has no inverse element), and their elements also obey distributivity. Such sets are called number fields.
Definition 2.8 Field
A set $(\mathbb{F}, +, \cdot)$ is called a field
with neutral elements $0$ and $1$ for addition $+$ and multiplication $\cdot$, respectively,
when its elements comply with the following rules
a) $( \mathbb{F}, + )$ is a commutative group,
b) $( \mathbb{F} \backslash \{ 0 \}, \cdot )$ is a commutative group,
c) Addition and Multiplication are distributive:
$\forall a, b, c \in \mathbb{F} : a \cdot (b + c) = a \cdot b + a \cdot c$
Remark 2.8 For the multiplication of field elements one commonly suppresses the $\cdot$ for the multiplication, writing e.g. $a\,b$ rather than $a \cdot b$.
Example 2.12 The smallest field has two elements
The smallest field $(\{ 0, 1 \} , \oplus, \odot)$ comprises only the neutral elements
$0$ of the group $(\{ 0, 1 \} , \oplus )$ with two elements, and
$1$ of the group $(\{ 1 \} , \odot )$ with one element.
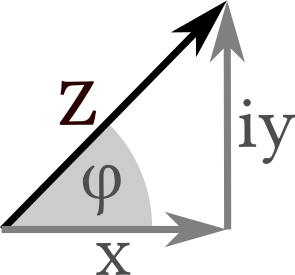
Figure 2.8 Complex numbers $z$ can be represented as $z=x+\mathrm{i} y$ in a plane where $(x,y)$ are the Cartesian coordinates of $z$. Alternatively, one can adopt a representation in terms of polar coordinates $z = R \, \mathrm{e}^{\mathrm{i} \varphi}$ where $R = \sqrt{x^2+y^2}$ and $\varphi$ is the angle with respect to the $x$-axis.
Example 2.13 Complex numbers are a field
a) The sum of two complex numbers $z_1 = x_1 + \mathrm{i} y_1$ and
$z_2 = x_2 + \mathrm{i} y_2$ amounts to
\begin{align*}
z_1 + z_2
= ( x_1 + \mathrm{i} y_1) + (x_2 + \mathrm{i} y_2)
= (x_1 + x_2) + \mathrm{i} (y_1 + y_2)
\end{align*}
Hence, the group properties for $+$ follow from the properties of the real numbers $x_1$, $x_2$ and $y_1$, $y_2$, respectively.
b) They also entail distributivity of complex numbers.
c) The product of the complex numbers $z_1 = x_1 + \mathrm{i} y_1$ and
$z_2 = x_2 + \mathrm{i} y_2$ amounts to
\begin{align*}
z_1 \cdot z_2
& = ( x_1 + \mathrm{i} y_1 ) \cdot ( x_2 + \mathrm{i} y_2 )
\\
& = x_1 \, x_2 + x_1\, (\mathrm{i} y_2) + (\mathrm{i} y_1) \, x_2 + (\mathrm{i} y_1)\, (\mathrm{i} y_2)
\\
&= ( x_1\, x_2 - y_1\,y_2 ) + \mathrm{i} \, (x_1 \, y_2 + y_1 \, x_2)
\end{align*}
Checking the group axioms based on this representation of the complex numbers is tedious.
One better adopts a representation in terms of polar coordinates,
$z_1 = R_1 \, \mathrm{e}^{\mathrm{i} \varphi_1}$ and $z_2 = R_2 \, \mathrm{e}^{\mathrm{i} \varphi_2}$
(see Figure 2.8) where (cf Problem 2.10)
\begin{align*}
z_1 \cdot z_2
= R_1 \, \mathrm{e}^{\mathrm{i} \varphi_1} \cdot R_2 \, \mathrm{e}^{\mathrm{i} \varphi_2}
= \bigl( R_1 \, R_2 \bigr) \: \mathrm{e}^{\mathrm{i} \, (\varphi_1+\varphi_2)}
\end{align*}
Here, the group properties follow from those of multiplying $R_1$ and $R_2$,
and adding $\varphi_1$ and $\varphi_2$.
Remark 2.9 [complex conjugation]
Each complex numbers $z$ has a complex conjugate, denoted as $z^*$ or $\bar z$,
that is defined as
$\forall z = x+\mathrm{i} y = R \, \mathrm{e}^{\mathrm{i} \varphi} \in \mathbb{C} : \quad
\bar z = x - \mathrm{i} y = R \; \mathrm{e}^{-\mathrm{i} \varphi} $
Complex conjugation provides an effective way to calculate the absolute value $|z|=R$ of complex numbers
\begin{align*}
z \, \bar z &= (x + \mathrm{i} y) \: (x - \mathrm{i} y) = x^2 - \mathrm{i}^2 \, y^2 = x^2 + y^2 = R^2 \text{ and }
\end{align*}
\begin{align*}
z \, \bar z &= R \, \mathrm{e}^{\mathrm{i} \varphi} \; R \, \mathrm{e}^{-\mathrm{i} \varphi} = R^2 \, \mathrm{e}^0 = R^2
\end{align*}
\begin{align*}
\Rightarrow \quad |z| &= \sqrt{z \, \bar z} = \sqrt{ \bar z \, z}
\end{align*}
Remark 2.10 In physics complex numbers are commonly applied to describe rotations in a plane: Multiplication by $\mathrm{e}^{\mathrm{i}\theta}$ rotates a complex number $z$ by an angle $\theta$ around the origin: \begin{align*} \forall z = R \, \mathrm{e}^{\mathrm{i} \varphi} \in \mathbb{C} : \quad z \cdot \mathrm{e}^{\mathrm{i}\theta} = R \, \mathrm{e}^{\mathrm{i} (\varphi+\theta)} \end{align*}
2.4.1 Self Test
Problem 2.9: Checking field axioms
Which of the following sets are fields?
1. $( \mathbb{Z}, +, \cdot )$
2. $( \{ 1, 2, \dots , 12 \}, + \text{mod} 12, \cdot \text{mod} 12)$
like on a clock: $11 \oplus 2 = 13 \text{mod} 12= 1$ and $4 \odot 5 = 20 \text{mod} 12= 8$.
3. $( \{ 0, 1, 2 \}, + \text{mod} 3, \cdot \text{mod} 3)$
for instance $2\odot 2 = 2 + 2 = 4 \text{mod} 3 = 1$ and $2 \oplus 1 = 3 \text{mod} 3 = 0$.
Problem 2.10: Euler's equation and trigonometric relations
Euler's equation $\mathrm{e}^{\mathrm{i} x} = \cos x + \mathrm{i} \: \sin x$
relates complex values exponential functions and trigonometric functions.
1. Sketch the position of $R\, \mathrm{e}^{\mathrm{i} x}$ in the complex plane, and indicate how Euler's equation is related to the Theorem of Pythagoras.
2. Complex valued exponential functions obey the same rules as their real-valued cousins. In particular, for $R=1$ one has $\mathrm{e}^{\mathrm{i} \, (x+y)} = \mathrm{e}^{\mathrm{i} x} \: \mathrm{e}^{\mathrm{i} y}$. Compare the real and complex parts of the expressions on both sides of this relation. What does this imply about $\sin( 2 x )$ and $\cos( 2 x )$?