2. Balancing Forces and Torques
- 2.3 Groups
2.3 Groups
A group $G$ refers to a set of operations $t\in G$ that are changing some data or objects. Elementary examples refer to reflections in space, turning some sides of a Rubik's cube, or translations in space, as illustrated in Figure 2.1. The subsequent action of two group elements $t_1$ and $t_2$ of $G$ is another (typically more complicated) transformation $t_3 \in G$. Analogous to the concatenation of functions, we write $t_3 = t_2 \circ t_1$, and we say $t_3$ is $t_2$ after $t_1$. The set of transformations forms a group iff it obeys the following rules.
Definition 2.6 Group
A set $(G, \circ)$ is called a group with operation $\circ: G \times G \to G$
when the following rules apply
- a) The set is closed: $\quad \forall g_1, g_2 \in G : g_1 \circ g_2 \in G$.
- b) The set has a neutral element: $\quad \exists e \in G \; \forall g \in G: e \circ g = g$.
- c) Each element has an inverse element: $\quad \forall g \in G \; \exists i \in G : i \circ g = e$.
- d) The operation $\circ$ is associative: $\quad \forall g_1, g_2, g_3 \in G : ( g_1 \circ g_2 ) \circ g_3 = g_1 \circ ( g_2 \circ g_3 )$.
Definition 2.7 Commutative Group
A group $(G, \circ)$ is called a commutative group when
- e) the group operation is commutative: $\forall g_1, g_2 \in G : g_1 \circ g_2 = g_2 \circ g_1$.
Remark 2.5. Commutative groups are also denoted as Abelian groups.
When the group has a finite number of elements the result of the group operation can explicitly be specified by a group table. We demonstrate this by the smallest groups. The empty set can not be a group because it has no neutral element. Therefore the smallest groups have a single element and two elements. Both of these groups are commutative.
Example 2.8 Smallest groups
$(\{ n \}, \odot)$ comprises only the neutral element.
| $\odot$ | $n$ |
|---|---|
| $n$ | $n$ |
The smallest non-trivial group has two elements $(\{ 0, 1\}, \oplus)$ with
| $\oplus$ | $0$ | $1$ |
|---|---|---|
| $0$ | $0$ | $1$ |
| $1$ | $1$ | $0$ |
It describes the turning of a piece of paper:
- Not turning, $0$, does not change anything (neutral element).
- Turning, $1$, shows the other side, and turning twice is equivalent to not turning at all ($1$ is its own inverse).
Remark 2.6. The group properties imply that all elements of the group must appear exactly once in each row and each column of the group table. As a consequence the smallest non-commutative group is the dihedral group of order 6 with six elements that is discussed in Problem 2.7.
Example 2.9 Non-commutative groups: rotations
The rotation of an object in space is a group.
In particular this holds for the $90^\circ$-rotations of an object around a vertical and a horizontal axis.
Figure 2.6 illustrates that these rotations do not commute.
 first horizontal, then vertical.
first horizontal, then vertical.
 first vertical, then horizontal.
first vertical, then horizontal.
Figure 2.6: Rotation of a book by $\pi/2$ around a vertical and a horizontal axes.
$\quad$
Remark 2.7. Notations and additional properties:
- Depending of the context the inverse element is denoted as $g^{-1}$ or as $-g$. This depends on whether the operation is considered a multiplication or rather an addition. In accordance with this choice the neutral element is denoted as $1$ or $0$.
- The second property of groups, b) $\exists e \in G \; \forall g \in G: e \circ g = g$, implies that also $g \circ e = g$. The proof is provided as Problem 2.8.
- When a group is not commutative then one must distinguish the left and right inverse. The condition $g \circ i = e$ does not imply $i \circ g = e$. However, there always is another element $j \in G$ such that $j \circ g = e$. An example is provided in Problem 2.7.
2.3.3 Self Test
Problem 2.4: Checking group axioms
Which of the following sets are groups?
- $( \mathbb{N}, + )$
- $( \mathbb{Z}, + )$
- $( \mathbb{Z}, \cdot )$
- $( \{+1, -1\}, \cdot )$
- $( \{ 0 \}, + )$
$( \{ 1, \dots, 12 \}, \oplus )$ where $\oplus$ refers to adding as we do it on a clock, e.g. $10 \oplus 4 = 2$.
Problem 2.5: The group with three elements
Let $(\mathcal G, \circ)$ be a group with three elements $\{n,l,r\}$,
where $n$ is the neutral element.
- Show that there only is a single choice for the result of the group operations $a \circ b$ with $a,b \in \mathcal G$. Provide the group table.
- Verify that the group describes the rotations of an equilateral triangle that interchange the positions of the angles.
- Show that there is a bijective map $\mathrm{m}:\{n,l,r\} \to \{0,1,2\}$ with the following property:
\[ \forall a,b \in \mathcal G : \mathrm{m}(a \circ b) = \bigl( \mathrm{m}(a) + \mathrm{m}(b) \bigr) \mathrm{mod} 3 \] We say that the group $\mathcal G$ is isomorphic to the natural numbers with addition modulo 3.1)
Problem 2.6: Symmetry group of rectangles
A polygon has a symmetry with an associated symmetry operation $a$ when $a$ only interchanges the vertices of the polygon. It does not alter the position. To get a grip on this concept we consider the symmetry operations of a rectangle.
- Sketch how reflections with respect to a symmetry axis interchange the vertices of a rectangle. What happens when the reflections are repeatedly applied?
- Show that the symmetry operations form a group with four elements. Provide a geometric interpretation for all group elements.
- Provide the group table.
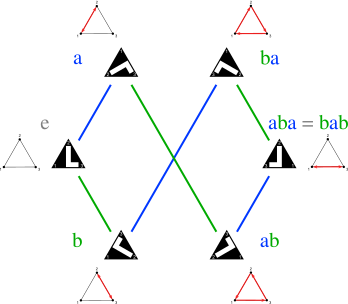 Watchduck (a.k.a. Tilman Piesk), wikimedia, CC BY-SA
Watchduck (a.k.a. Tilman Piesk), wikimedia, CC BY-SA
Figure 2.7: Reflections of equilateral triangle with respect to the three symmetry axes form a group with six elements; see Problem 2.7.
Watch out: in this figure the operations are carried out from left to right:
$ab$ refers here to $b$ after $a$, in contrast to the convention introduced in the beginning of the present section.
Problem 2.7: Dihedral group of order $6$
Figure 2.7 illustrates the effect of reflections of a triangle with respect to its three symmetry axis. All group elements can be generated by repeated action of two reflections, e.g. those denoted as $a$ and $b$ in the figure.
- Verify that the group properties, Definition 2.6, together with the three additional requirements \[ a \circ a = b \circ b = e \quad\text{and}\quad a \circ b \circ a = b \circ a \circ b \] imply that the group has exactly six elements, \[ \mathcal G = \{ e, a, b, a\circ b, b\circ a, a\circ b\circ a \} \,. \]
- Work out the group table.
- Verify by inspection that $e$ is the neutral element for operation from the right and from the left.
- Verify that the group is not commutative, and provide an example of a group element where the left inverse and the right inverse differ.
- The group can also be represented in terms of a reflection and the rotations described in Problen 2.5. How would the graphical representation, analogous to Figure 2.7, look like in that case.
Problem 2.8: Uniqueness of the neutral element
Proof that the group axioms, Definition 2.6, imply that $e \circ g = g$ implies that also $g \circ e = g$.
