2. Balancing Forces and Torques
- 2.6. Physics application: balancing forces
2.6 Physics application: balancing forces
Tug of War, Nikolay Bogdanov-Belsky, 1939
wikiart / public domain
It is an experience from tug of war that nothing moves as long as forces are balanced. In this example one can add a ring to the rope. The pulling forces act in opposing directions on the ring, as illustrated in the upper left diagram in Figure 2.10. The lower left diagram shows the case, where three parties are pulling on the ring. In any case the total force on the ring amounts to the sum of the acting forces, forces are vectors, and all sums of vectors obey the same rules. As far as graphical illustrations are concerned the sum of forces looks therefore the same as the sum of displacements in Figure 2.1. For the ring the sums of the forces are illustrated in the right panels of Figure 2.10. The ring does not move when they add to zero.
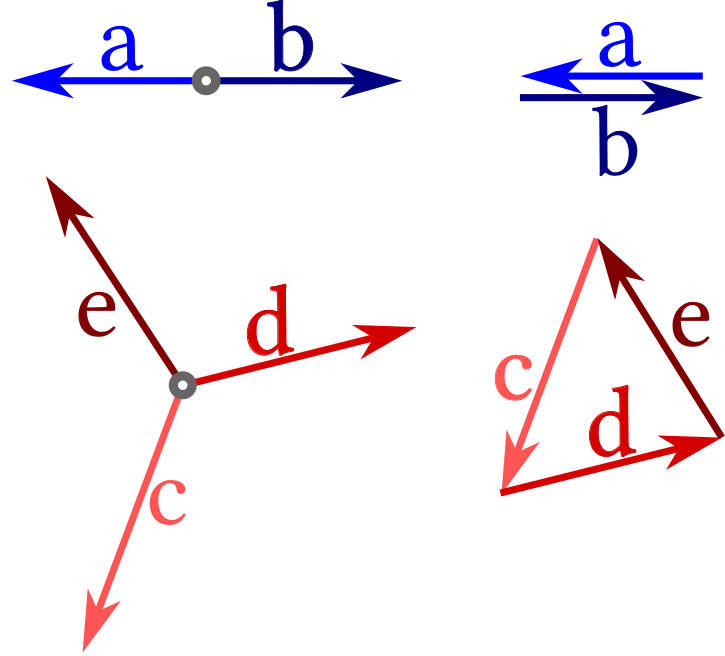Figure 2.10: The left diagrams show two and three forces acting on a ring. To the right it is demonstrated that they add to zero.
Axiom 2.1: Force balance
Let $N$ forces $\mathbf F_1, \dots, \mathbf F_N$ act on a body.
The body does not move as long as the forces add to zero,
i.e. iff
$\displaystyle \mathbf 0 = \sum_{i=1}^N \mathbf F_i$.
Remark 2.15 Strictly speaking the body might turn, but its center of mass will not move. We come back to this point in Section 2.9.
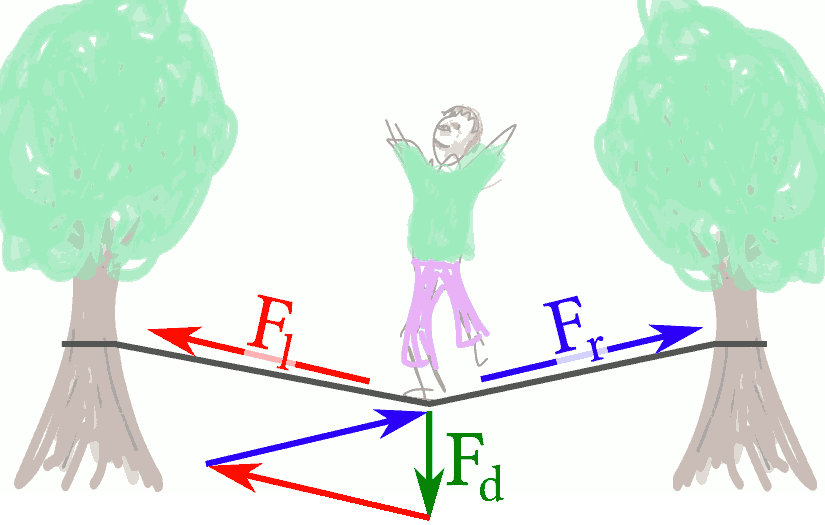Figure 2.11: For a person balancing on a slackline, the gravitational force $\mathbf F_d$ (d for down)
is balanced by forces $\mathbf F_l$ and $\mathbf F_r$ along the line that pull towards the left and right, respectively. See Example 2.19 for further discussion.
Example 2.19 Balancing on a slackline
A person balances on a slackline that is fixed to trees at its opposing sides.
At the point where she is standing there are three forces acting: her weight $\mathbf F_d = M \mathbf g$ pushing downwards, and forces along the slackline towards the left $\mathbf F_l$ and right $\mathbf F_r$. She can stay at rest as long as
\begin{align*}
\mathbf 0 = \mathbf F_d + \mathbf F_l + \mathbf F_r
\end{align*}
The forces $\mathbf F_l$ and $\mathbf F_r$ are counterbalanced by the trees.
These forces become huge when the slackline runs almost horizontally.
Every now a then a careless slackliner roots out a tree or fells a pillar.
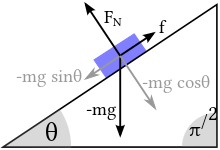
Figure 2.12: (top) As long as $\theta$ is smaller than the angle of friction the blue block does not slide.
(bottom) Placing my cell phone on two rubber bands on a folder provides a maximum angle of about$33^{\circ}$,
i.e., $\mu \simeq 0.5$.
Using PhyPhox and a cell phone one can easily measure $\theta_c$ and $\mu$ for other combinations of materials.
Example 2.20: Measuring the static friction coefficient
In a rough approximation static friction between two surfaces arises due to interlocking or surface irregularities.
One must lift a block by a little amount to unlock the surfaces.
In line with this argument dimensional analysis suggest that static friction should be proportional to the normal force between the surfaces.
It is independent of the contact area, and depends on the material of the surfaces.
This is indeed what is observed experimentally:
The static friction force, $\mathbf f$ in Figure 2.12,
can take values up to a maximum value of $\gamma$ times the normal force, $\mathbf F_N$,
where $\gamma$ typically takes values slightly less than one.
By splitting the gravitational force, $m\mathbf g$ acting on a block on a plane into its components parallel and normal to the surface (gray arrows in Figure 2.12),
one finds that in the presence of a force balance $m \mathbf g + \mathbf f + \mathbf F_N = \mathbf 0$
one has
\begin{align*}
\left .
\begin{aligned}
F_N &= m g \, \cos\theta \\
f &= m g \, \sin\theta \\
f &< \gamma F_N
\end{aligned}\right\}
\quad
\begin{aligned}
\Rightarrow \sin\theta &< \gamma\cos\theta \\
\Rightarrow \theta &< \theta_c = \arctan\gamma
\end{aligned}
\end{align*}
When $\theta$ exceeds $\theta_c$ the block starts to slide.
Hence, one can infer $\gamma$ from measurements of $\theta_c$.
2.6.1 Self Test
Problem 2.14: Particles at rest
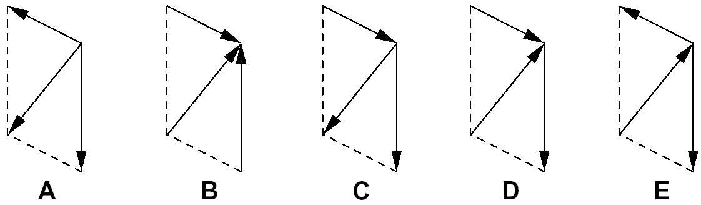
There are three forces acting on the center of mass of a body. In which cases does it stay at rest?
Problem 2.15: Graphical sum of vectors
Determine the sum of the vectors. In which cases is the resulting vector vertical to the horizontal direction?
Problem 2.16: Towing a stone
Three Scottish muscleman 1) try to tow a stone with mass $M=20\text{cwt}$ from a field. Each of them gets his own rope, and he can act a maximal force of
$300\text{lbg}$ as long as the ropes run in directions that differ by at least $30^\circ$
- Sketch the forces acting on the stone and their sum. By which ratio is the force exerted by three men larger than that of a single man?
- The stone counteracts the pulling of the men by a static friction force $\mu M g$, where $g$ is the gravitational acceleration. What is the maximum value that the friction coefficient $\mu$ may take when the men can move the stone?