2. Balancing Forces and Torques
- 2.7 The inner product
2.7 The inner product
The position of a particle, the direction of its motion and the angle of attack of forces are constantly changing during the motion of a particle. In Chapter 3 we explore how they are related. The calculations are feasible because the involved vector spaces also have an inner product.
Definition 2.12 Inner Product of vector spaces over $\mathbb{R}$ or $\mathbb{C}$
The inner product on a vector space $(\mathsf{V}, \mathbb{R}, \oplus, \odot)$ defines
a binary operation $\langle \, \_ \! \mid \! \_ \, \rangle : \mathsf{V} \times \mathsf{V} \to \mathbb{R}$
with the following properties for all $\mathbf u, \mathbf v, \mathbf w \in \mathsf{V}$ and $c \in \mathbb{R}$
a) commutativity:
$\langle \mathbf v \mid \mathbf w \rangle = \langle \mathbf w \mid \mathbf v \rangle$
b) linearity in the first argument:
$\langle c \odot \mathbf v \mid \mathbf w \rangle = c \; \langle \mathbf v \mid \mathbf w \rangle$
and $\langle \mathbf u \oplus \mathbf v \mid \mathbf w \rangle = \langle \mathbf u \mid \mathbf w \rangle + \langle \mathbf v \mid \mathbf w \rangle$
c) positivity:
$\langle \mathbf v \mid \mathbf v \rangle \geq 0$
where equality applies iff $\mathbf v = \mathbf 0$,
$\langle \mathbf v \mid \mathbf v \rangle = 0 \;\Leftrightarrow\; \mathbf v = \mathbf 0$
For a vector space over $\mathbb{C}$ the inner product returns a complex number, and the constant $c$ is a complex number. Moreover, the requirement a) is replaced by
a) conjugate symmetry: $\langle \mathbf v \mid \mathbf w \rangle = \overline{\langle \mathbf w \mid \mathbf v \rangle}$
such that $\langle \mathbf v \mid \mathbf v \rangle$ is a real number.
Remark 2.16 The idea underlying these properties is that $\sqrt{\langle \mathbf v \mid \mathbf v \rangle}$ can be interpreted as the length of the vector $\mathbf v$.
Remark 2.17 Conjugate symmetry and linearity for the first argument imply the following relations for the second argument \begin{align*} \langle \mathbf v \mid c \odot \mathbf w \rangle &= \overline{\langle c \odot \mathbf w \mid \mathbf v \rangle} = \bar{c} \;\overline{\langle \mathbf w \mid \mathbf v \rangle} = \bar{c} \; \langle \mathbf v \mid \mathbf w \rangle \end{align*} \begin{align*} \langle \mathbf u \mid \mathbf v \oplus \mathbf w \rangle &= \overline{\langle \mathbf v \oplus \mathbf w \mid \mathbf u \rangle} = \overline{\langle \mathbf v \mid \mathbf u \rangle} + \overline{\langle \mathbf w \mid \mathbf u \rangle} = \langle \mathbf u \mid \mathbf v \rangle + \langle \mathbf u \mid \mathbf w \rangle \end{align*}
Remark 2.18
Certain properties that hold for addition and scalar multiplication do
not hold for the inner product.
a) There is no inverse: The information about the direction of vectors is lost upon taking the inner product. For instance, when $\langle\mathbf{u} \mid \mathbf{v} \rangle = 0$ and $\langle \mathbf{u} \mid \mathbf{w} \rangle = 0$ then one still can not tell the result of $\langle \mathbf{v} \mid \mathbf{w} \rangle$.
b) Associativity does not hold: $\langle \mathbf{u} \mid \mathbf{v} \rangle \: \mathbf{w} \neq \mathbf{u} \: \langle \mathbf{v} \mid \mathbf{w} \rangle$.
Example 2.21 Inner product for real-valued vectors
For real-valued vectors the inner product is commutative, $\langle \mathbf v \mid \mathbf w \rangle = \langle \mathbf w \mid \mathbf v \rangle$. The inner product is then also be written as $\mathbf v \cdot \mathbf w$,
and it obeys bilinearity
\begin{align*}
\mathbf{u}\cdot (a\mathbf{v}+ b\mathbf{w})=a(\mathbf{u}\cdot \mathbf{v}) + b (\mathbf{u}\cdot \mathbf{w})
\end{align*}
Theorem 2.2 Geometric Interpretation of the Inner Product for Real-Valued Vectors
For vectors of $\mathbb{R}^D$ the inner product of two vectors $\mathbf a$, $\mathbf b$
takes the value
\begin{align*}
\mathbf a \cdot \mathbf b = |\mathbf a| \: |\mathbf b| \: \cos\theta
\end{align*}
where $\theta = \angle(\mathbf a, \mathbf b)$ is the angle between the two vectors, see Figure 2.13.
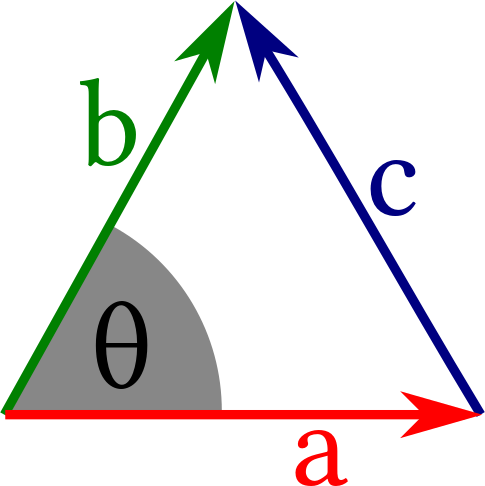 Figure 2.13: Notations for the geometric interpretation of the inner product,
Theorem 2.2
Figure 2.13: Notations for the geometric interpretation of the inner product,
Theorem 2.2
Proof. The cosine theorem for triangles with sides of length $a$, $b$ and $c$ and angle $\theta$ opposite to $c$ states that \begin{align*} c^2 = a^2 + b^2 - 2\,a\,b\,\cos\theta \end{align*} Let now $a$, $b$, and $c$ be the length of the vectors $\mathbf a$, $\mathbf b$ and $\mathbf c = \mathbf b - \mathbf a$, as shown in Figure 2.13. Then we have \begin{align*} a^2 + b^2 - 2\,a\,b\,\cos\theta &= c^2 = \mathbf c \cdot \mathbf c = (\mathbf b - \mathbf a) \cdot (\mathbf b - \mathbf a) = (\mathbf a - \mathbf b) \cdot (\mathbf a - \mathbf b) \\ &= \mathbf a \cdot \mathbf a - 2\, \mathbf a \cdot \mathbf b + \mathbf b \cdot \mathbf b = a^2 + b^2 - 2\, \mathbf a \cdot \mathbf b \\[2mm] \Rightarrow\quad \mathbf a \cdot \mathbf b &= |\mathbf a| \, |\mathbf b| \, \cos\theta \\ \end{align*}
Remark 2.19 Theorem 2.2 entails that the inner product $\mathbf u \cdot \mathbf v$ vanishes when the vectors are orthogonal, $\theta=\pi/2$. Also in general we say that \begin{align*} \text{$\mathbf v$ and $\mathbf w$ are othogonal iff} \qquad \langle \mathbf v \mid \mathbf w \rangle = 0 \, . \end{align*}
Remark 2.20 The expression for the inner product that is provided in Theorem 2.2 does not imply that the inner product is unique. Rather it is a consequence of the cosine theorem that holds iff the geometric interpretation of the vectors applies. This is demonstrated by an example provided in Problem 2.17.
2.7.1 Self Test
Problem 2.17: The inner product is not unique
Let $\mathbf v_1$ and $v_2$ be two non-orthogonal vectors in a two-dimensional vector space with an inner product $\langle \_ \mid \_ \rangle$,
and let $\lambda_1$ and $\lambda_2$ two positive real numbers.
Then the following relation defines another inner product $( \_ \mid \_ )$:
\begin{align*}\label{eq:nonUniqueInnerProd}
( \mathbf a \mid \mathbf b )
= \lambda_1 \langle \mathbf a \mid \mathbf e_1 \rangle \: \langle \mathbf e_1 \mid \mathbf b \rangle
+ \lambda_2 \langle \mathbf a \mid \mathbf e_2 \rangle \: \langle \mathbf e_2 \mid \mathbf b \rangle
\end{align*}
- Verify that the properties a) and b) of an inner product $\langle \_ \mid \_ \rangle$ as given in Definition 2.12 are also be obeyed by $( \_ \mid \_ )$.
- Verify that $( \mathbf a \mid \mathbf a ) \geq 0$ iff $\lambda_1$ and $\lambda_2$ two positive real numbers.
- Verify that $( \mathbf a \mid \mathbf a ) = 0$ implies $\mathbf a = \mathbf 0$ iff the vector space is two-dimensional.
Problem 2.18: Inner products for polynomials
Let
$\mathbf p = \left[\sum_{i=0}^D p_i \, x^i\right]$ and
$\mathbf q = \left[\sum_{i=0}^D q_i \, x^i\right]$
be elements of the vector space of $N$-dimensional polynomials.
Verify that the following rules define inner products on this space.
- $\displaystyle \langle \mathbf p \mid \mathbf q \rangle = \sum_{i=0}^N \bar p_i \, q_i$
- $\displaystyle \langle \mathbf p \mid \mathbf q \rangle_{[a,b]} = \displaystyle \int_a^b \mathrm{d} x \overline{\left[\sum_{i=0}^D p_i \, x^i\right]} \; \left[\sum_{i=0}^D q_i \, x^i\right]$, for $a < b \in \mathbb{R}$
- Show that $\mathbf p = [1]$ and $\mathbf q = [x]$ are orthogonal with respect to the inner product defined in 1). Under which condition are they also orthogonal for the inner product defined in 2)?
