2. Balancing Forces and Torques
- 2.5 Vector spaces
2.5 Vector spaces
With the notions introduced in the preceding sections we can give now the formal definition of a vector space
Definition 2.9 Vector Space
A vector space $(\mathsf{V}, \mathbb{F}, \oplus, \odot)$ is
a set of vectors $\mathbf v \in \mathsf{V}$
over a field $(\mathbb{F}, +, \cdot)$
with binary operations
$\oplus : \mathsf{V} \times \mathsf{V} \to \mathsf{V}$ and $\odot : \mathbb{F} \times \mathsf{V} \to \mathsf{V}$
complying with the following rules
- $(\mathsf{V}, \oplus )$ is a commutative group
- associativity: $\forall a,b \in \mathbb{F} \; \forall \mathbf v \in \mathsf{V} : a \odot ( b \odot \mathbf v ) = ( a \cdot b) \odot \mathbf v$
- distributivity 1: \( \forall a,b \in \mathbb{F} \; \forall \mathbf v \in \mathsf{V} : (a + b) \odot \mathbf v = ( a \odot \mathbf v) \oplus ( b \odot \mathbf v) \)
- distributivity 2: \( \forall a \in \mathbb{F} \; \forall \mathbf v, \mathbf w \in \mathsf{V} : a \odot (\mathbf v \oplus \mathbf w ) = ( a \odot \mathbf v) \oplus ( a \odot \mathbf w) \)
Remark 2.11 It is common to use $+$ and $\cdot$ instead of $\oplus$ and $\odot$, respectively, with the understanding that it is clear from the context in the equation whether the symbols refer to operations involving vectors, only numbers, or a number and a vector. Moreover, as for the multiplication of numbers, one commonly drops the $\odot$ for the multiplication, writing e.g. $a \, \mathbf v$ rather than $a \cdot \mathbf v$.
Example 2.14 Vector spaces: displacements in the plane
For displacements we define the operation $\oplus$ as concatenation of displacements,
and $\odot$ as increasing the length of the displacement by a given factor without touching the direction.
a) The neutral element amounts to staying, one can always shift back, move between any two points in a plane,
and commutativity follows form the properties of parallelograms, see Figure 2.9.
b) The vectors select the direction.
c) Scalar multiplication only changes the length of the vectors, and the length is a real number.
d) Is implied by the Intercept Theorem.
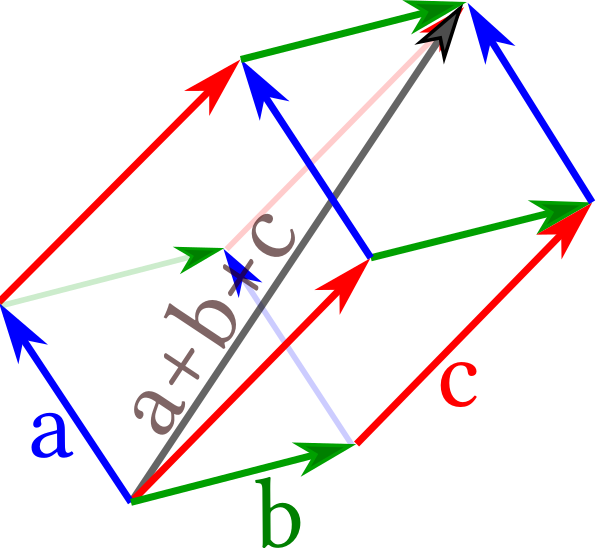Figure 2.9: The arrows indicate displacements by three vectors $\mathbf a$, $\mathbf b$ and $\mathbf c$, as discussed in Example 2.14.
Their commutativity and associativity follow from the properties of parallelograms.
This holds in the plane, and also when the vectors span a three-dimensional volume.
Example 2.15 Vector spaces: $\mathbb{R}^D$
For every $D \in \mathbb{N}$ the $D$-fold Cartesian product $\mathbb{R}^D$ of the
real numbers is a vector space over $\mathbb{R}$ when defining the operation $+$ and $\cdot$ as
\begin{align*} \forall \mathbf a, \mathbf b \in \mathbb{R}^D : \mathbf a + \mathbf b &= \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_D \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_D \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \\ \vdots \\ a_D + b_D \end{pmatrix} \\ \forall s \in \mathbb{R} \; \forall \mathbf a \in \mathbb{R}^D : s \cdot \mathbf a &= s \; \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_D \end{pmatrix} = \begin{pmatrix} s \, a_1 \\ s \, a_2 \\ \vdots \\ s \, a_D \end{pmatrix} \end{align*} In a more compact manner this is also written as, \begin{align*} \forall \mathbf a=(a_i), \mathbf b = (b_i), s \in\mathbb{R} : \mathbf a + \mathbf b = (a_i+b_i) \; \land \; s\, \mathbf a = (s\,a_i) \end{align*} Checking the properties of a vector space is given as Problem 2.11 a).
Definition 2.10 $N\times M$ Matrix: $\mathbb{M}^{N\times M}(\mathbb{F})$
For $N,M \in \mathbb{N}$ we define $N\times M$ matrices $A, B \in \mathbb{M}^{N\times M}(\mathbb{F})$
over the field $\mathbb{F}$
as arrays, $A=(a_{ij})$, $B=(b_{ij})$,
with components $a_{ij}, b_{ij}, \in \mathbb{F}$.
The indices
$i \in \{ 1, \dots, N \}$ and
$j \in \{ 1, \dots, M \}$
label the rows and columns of the array, respectively.
The sum of matrices and the product with a scalar are defined component-wise as
\begin{align*}
\forall A, B \in \mathbb{M}^{N\times M}, \; c \in \mathbb{F} :
A+B = (a_{ij}+b_{ij})
\; \land \;
c \cdot A = \left( c \, a_{ij} \right)
\end{align*}
Example 2.16 $3\times 2$ matrices: summation and multiplication with a scalar
To be specific we provide here the sum of two $3\times 2$ matrices and the multiplication by a factor of $\pi$.
Let
\begin{align*}
A &= \begin{pmatrix}
2 & 3 \\
4 & 5 \\
6 & 7
\end{pmatrix}
\quad \text{and} \quad
B = \begin{pmatrix}
12 & 13 \\
14 & 15 \\
16 & 17
\end{pmatrix} \, .
\end{align*}
Then
\begin{align*}
A + B &= \begin{pmatrix}
2+12 & 3+13 \\
4+14 & 5+15 \\
6+16 & 7+17
\end{pmatrix}
= \begin{pmatrix}
14 & 16 \\
18 & 20 \\
22 & 24
\end{pmatrix}
\\
\pi \: A &= \begin{pmatrix}
2 & 3 \\
4 & 5 \\
6 & 7
\end{pmatrix}
= \begin{pmatrix}
2 \, \pi & 3 \, \pi \\
4 \, \pi & 5 \, \pi \\
6 \, \pi & 7 \, \pi
\end{pmatrix}
\end{align*}
Example 2.17 Vector spaces: $M\times N$ matrices
The $N\times M$ matrices over a field $\mathbb{F}$, $(\mathbb{M}^{N\times M}, \mathbb{F}, +, \cdot)$
form a
vector space.
The proof is given as Problem 2.11 b).
Definition 2.11 Matrix multiplication
For matrices one defines a product as follows
\begin{align*}
\odot &: \mathbb{M}^{N\times L} \times \mathbb{M}^{L\times M}\to \mathbb{M}^{N\times M}
\\
\forall A \in \mathbb{M}^{N\times L}, B \in \times \mathbb{M}^{L\times M} &:
A \odot B = C = (c_{ij}) = \left( \sum_{k=1}^L a_{ik} b_{kj} \right)
\end{align*}
Remark 2.12 Also for matrix multiplication one commonly suppresses the $\odot$ operator, writing $A\,B$ rather than $A \odot B$.
Remark 2.13 For square matrices $\mathbb{M}^{M\times M}$ the operation $+$ and $\odot$ define a sum and a product that take two elements of $\mathbb{M}^{M\times M}$ and return an element of $\mathbb{M}^{M\times M}$. Nevertheless, $(\mathbb{M}^{M\times M}, + , \odot)$ is not a field: In general, $\odot$ is not commutative and matrices do not necessarily have an inverse.
Remark 2.14 Square matrices can be used to represent reflections and rotations. In Problem 2.12 we provide an example of eight matrices that form a symmetry group.
Example 2.18 Vector spaces: Polynomials of degree $2$
For a field $\mathbb{F}$ the polynomials $\mathsf{P}_2$ of degree two in the variable $x$ are defined as
\begin{align*}
\mathsf{P}_2 = \{ \mathbf p = [ p_0 + p_1 \: x + p_2 \: x^2 ] : p_0, p_1, p_2 \in \mathbb{F} \}
\end{align*}
This set is a vector space with respect to the summation
\begin{align*}
\mathbf p + \mathbf q
&= [ p_0 + p_1 \: x + p_2 \: x^2 ] + [ q_0 + q_1 \: x + q_2 \: x^2 ]
\\
&= \Bigl[ (p_0+ q_0) + (p_1 + q_1) \: x + (p_2 +q_2) \: x^2 \Bigr]
\end{align*}
and the multiplication with a scalar $s \in \mathbb{F}$
\begin{align*}
s \cdot \mathbf p
= s \cdot ( p_0 + p_1 \: x + p_2 \: x^2 )
= \Bigl[ (s\, p_0) + (s\, p_1) \: x + (s \, p_2) \: x^2 ) \Bigr]
\end{align*}
proof:
Each element $\mathbf p = [ p_0 + p_1 \: x + p_2 \: x^2 ]$
of this
vector space is uniquely described by the three-tuple $(p_0, p_1, p_2) \in \mathbb{F}^3$
with rules for addition and scalar multiplication analogous to those discussed for $\mathbb{R}^3$
in Example 2.15.
Hence, the proof for $\mathbb{R}^3$ also applies here.
In physics we heavily make use of the correspondence evoked by the proof in Example 2.18. The relative position of two objects with respect to each other is commonly described in terms of (the sum of several) vectors. In order to gain further information about the positions, we will then recast the geometric problem about the positions into an algebraic problem stated in terms of linear equations. The latter can then be solved by straightforward analytical calculations. Vice versa, abstract findings about the solutions of sets of equations will be recast in terms of geometry in order to visualize the abstract results. The change of perspective has become a major avenue to drive theoretical physics throughout the 20$^{\text{th}}$ century. For mechanical problems it forms the core of the mathematical formulation of problems in robotics and computer vision. Quantum mechanics is entirely build on the principles of vector spaces and their generalization to Hilbert spaces. General relativity and quantum field theory take Noether's theorem as their common starting point, which is build upon concepts from group theory and the requirement that physical predictions must not change when taking different choices how to mathematically describe the system. An important concern of these notes is to serve as a training ground to practice the changing of mathematical perspective for the purpose of solving physics problem. As a first physical application we discuss now force balances. Then we resume the discussion of vector spaces, taking a closer look into the calculation of coordinates and distances.
2.5.1 Self Test
Problem 2.11: Checking vector-space properties
- Verify that $\mathbb{R}^D$ with the operations defined in Example 2.15 is a vector space.
- Verify that $N\times M$ matrices, as defined in Definition 2.10, form a vector space.
Problem 2.12: Geometric interpretation of matrices
We explore the set of the eight matrices
\begin{align*}
M = \left\{
\begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix},
\begin{pmatrix} 0 & c \\ d & 0 \end{pmatrix},
\quad\text{with } \quad a, b, c, d \in \{ \pm 1 \}
\right\}
\end{align*}
- 1. Let the action $\circ$ denote matrix multiplication. Verify that $(M, \odot)$ is a group with respect to matrix multiplication, as defined in Definition 2.11. We denote its neutral element as $\mathbb{I}$.
- 2. Show that the group has five non-trivial elements $s_1, \dots s_5$ that are self inverse:
\begin{align*} s_i \neq \mathbb{I} \quad \land \quad s_i \circ s_i = \mathbb{I} \quad \text{for } \quad i \in \{ 1, \dots 6 \} \, . \end{align*}
- 3. Show that the other two elements $d$ and $r$ obey $d \circ r = r \circ d = \mathbb{I}$,
that $r = d \circ d \circ d$, and
that $d = r \circ r \circ r$.
- 4. Show that the set of points $P = \{ (1,1), (-1,1), (-1,-1), (1,-1) \}$ is mapped to $P$ by the action of an element of the group:
\begin{align*} \forall m \in M \;\; \land \;\; p \in P : \quad p \circ m \in P \end{align*}
- 5. What is the geometric interpretation of the group $M$? Illustrate the action of the group elements in terms of transformations of a suitably chosen geometric object.
Problem 2.13: Polynomials of degree $N$
For a field $\mathbb{F}$ the polynomials $\mathsf{P}_N$ of degree $N$ in the variable $x$ are defined as \begin{align*} \mathsf{P}_N = \left\{ \mathbf p = \left[ \sum_{i=0}^N p_i \: x^i \right] : p_0, \dots, p_N \in \mathbb{F} \right\} \end{align*}
- State the rules of addition and multiplication with a scalar $s \in \mathbb{F}$ in analogy to the special case of $N=2$ discussed in Example 2.18.
- Verify that the polynomials of degree $N$ are a vector space.