Table of Contents
6.4 Several degrees of freedom and conservation laws
In Section 6.3 we discussed the EOM of systems with one degree of freedom.
In the present section this analysis is extended to systems with two and more degrees of freedom.
Again the discussion will be based on examples:
1. We first discuss uniform motion where there are no fores acting on the particle.
Here, we learn about the concept of cyclic observables,
and how momentum conservation is related to translation invariance.
2. Subsequently, we address the case of uniform acceleration.
In this case there only is translation invariance in the directions normal to the acceleration.
The according components of the momentum are still preserved.
3. For systems with harmonic, Hookian forces we explore the relation between rotation invariance and the conservation of angular momentum.
Moreover, we introduce the concepts of an effective potential and of a rotation barrier.
4. Finally, we discuss the spherical pendulum.
It constitutes an example with a generic, non-trivial coupling of the evolution of its different DOF.
We will learn how to exploit conservation laws to decompose the dynamics into distinct dynamics with a single
degree of freedom.
6.4.1 Force-free motion
When there are no forces acting on the particle we have \begin{align*} T &= \frac{m}{2} \: \dot{\mathbf x}^2 = \frac{m}{2} \; \sum_i \dot x_i^2\\ V &= 0 \end{align*} Note that the Lagrange function $\mathcal L = T-V$ only depends on the velocity $\dot{\mathbf q}$ and not on the position $\mathbf q$. As a consequence, the Euler-Lagrange equation for the coordinate $x_i$ requires that the acceleration of the particle vanishes, \begin{align*} m \: \ddot x_i = \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial \dot x_i } = \frac{ \partial\mathcal L }{ \partial x_i } = 0 \end{align*} Alternatively, one may also express this result in the form of momentum conservation (cf. Section 3.4.3), \begin{align*} \dot{\mathbf P} = \frac{\mathrm{d}}{\mathrm{d} t} \Bigl( m \: \dot{\mathbf x} \Bigr) = \frac{\mathrm{d}}{\mathrm{d} t} \nabla_{ \dot{\mathbf x} } \mathcal L = \nabla_{\mathbf x} \mathcal L = \mathbf 0 \end{align*} Momentum conservation therefore is an immediate consequence of the Euler-Lagrange equation for systems where the Lagrange function does not depend on the coordinates. The general case is summarized in the following definition:
Definition 6.10 Cyclic coordinates
A coordinate $q_i$ is called cyclic
when the Lagrange function depends only on its time derivative $\dot q_i$,
and not on$q_i$.
In that case
the associated Euler-Lagrange equation establishes a conservation law,
\begin{align*}
C = \frac{\partial \mathcal L}{\partial \dot q_i} \, .
\end{align*}
After all
\begin{align*}
\frac{\mathrm{d} \, C}{\mathrm{d} t}
= \frac{\mathrm{d}}{\mathrm{d} t} \; \frac{\partial \mathcal L}{\partial \dot q_i}
= \frac{\partial \mathcal L}{\partial q_i} = 0 \, .
\end{align*}
Remark 6.9. The constant value of $C$ is determined by the initial conditions on $\dot q_i$ and on the other coordinates.
Based on the concepts introduced in problem 4.35, this finding generalizes as follows to a translation-invariant dynamics of $N$ particles
Theorem 6.6 Momentum conservation and translation invariance
Let, $\mathbf q =( \mathbf q_i, i=1\dots N )$, be the Cartesian coordinate vector of $N$ particles with masses $m_i$
that reside at the positions $\mathbf q_i(t)$.
We consider a dynamics with conservative forces
that derive from an translation-invariant potential $V(\mathbf q, t) = \sum_{i<j} \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert , t \bigr)$.
Then the total momentum $\mathbf P = \sum_i m_i \: \dot{\mathbf q}_i$ is conserved.
Proof. The kinetic energy of the dynamics is \begin{align*} T = \sum_{i=1}^N \frac{m_i}{2} \: \dot{\mathbf q}_i^2 \end{align*} and by assumption $V(\mathbf q, t)$ does not depend on $\dot{\mathbf q}$. Hence, \begin{align*} \sum_k \nabla_{\dot{\mathbf q}_k} \mathcal L = \sum_k \nabla_{\dot{\mathbf q}_k} T = \sum_i \frac{m_i}{2} \: \left( \sum_k \nabla_{\dot{\mathbf q}_k} \dot{\mathbf q}_i^2 \right) = \sum_{i=1}^N m_i \: \dot{\mathbf q}_i = \mathbf P \end{align*} Consequently, the time derivative of $\mathbf P$ amounts to \begin{align*} \frac{\mathrm{d} \mathbf P}{\mathrm{d} t} = \frac{\mathrm{d}}{\mathrm{d} t} \sum_k \nabla_{\dot{\mathbf q}_k} \mathcal L = \sum_k \nabla_{\mathbf q_k} \mathcal L = - \sum_{i<j} \left( \sum_k \nabla_{\mathbf q_k} \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert, t \bigr) \right) \end{align*} since $T$ does not involve the coordinates $\mathbf q_k$. Now, we observe that \begin{align*} \nabla_{\mathbf q_k} = \lvert \mathbf q_i - \mathbf q_j \rvert = \left\{ \begin{aligned} \frac{ \mathbf q_i - \mathbf q_j }{ \lvert \mathbf q_i - \mathbf q_j \rvert } \quad& \text{for}\quad k=i \\ \frac{ \mathbf q_j - \mathbf q_i }{ \lvert \mathbf q_i - \mathbf q_j \rvert } \quad& \text{for}\quad k=j \\ 0 \qquad & \text{else} \end{aligned} \right . \end{align*} We denote the derivative of $\Phi(d,t)$ with respect to its $d$ as $\Phi'(d,t)$ and observe that the sum over $k$ will have two non-vanishing contributions, \begin{align*} \frac{\mathrm{d} \mathbf P}{\mathrm{d} t} &= - \sum_{i<j} \left[ \frac{ \mathbf q_i - \mathbf q_j }{ \lvert \mathbf q_i - \mathbf q_j \rvert } \; \Phi_{ij}'\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert, t \bigr) + \frac{ \mathbf q_j - \mathbf q_i }{ \lvert \mathbf q_i - \mathbf q_j \rvert } \; \Phi_{ij}'\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert, t \bigr) \right] \\ &= \mathbf 0 \\ \end{align*} qed
6.4.2 Free flight
A particle experiencing free flight is subject to a constant force, i.e., a force that is uniform in space and that does not depend on time. A common example is a particle of mass $m$ close to the Earth surface. The particle is subject to a constant acceleration $\mathbf g$ (Section 4.2) that gives rise to a potential \begin{align*} V(\mathbf q) &= -m\: \mathbf g \cdot \mathbf q \end{align*} For Cartesian coordinates $\mathbf q = (q_1,q_2,q_3)$ where the first coordinate axis is aligned antiparallel to $\mathbf g$ the Lagrange function takes the from \begin{align*} T &= \frac{m}{2} \: \Bigl( \dot q_1^2 + \dot q_2^2 + \dot q_3^2 \Bigr) \\ V &= m\,g\: q_1 \\ \mathcal L &= T-V = \frac{m}{2} \: \Bigl( \dot q_1^2 + \dot q_2^2 + \dot q_3^2 \Bigr) - m\,g\: q_1 \, . \end{align*} In this setting $q_2$ and $q_3$ are cyclic variables such that the corresponding components of the momentum, $\mathbf P = m \: \mathbf q$, are conserved, \begin{align*} \dot P_2 = \dot P_3 = 0 \, . \end{align*} Moreover, for the first component we find \begin{align*} m \: \ddot q_1 = \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial \dot q_1 } = \frac{ \partial\mathcal L }{ \partial q_1 } = m\, g \end{align*} such that we recover the EOM Equation 4.2.1 with the solution, Equation 4.2.2 The impact of constant external forces on a set of $N$ particles is discussed in Problem 6.10.
6.4.3 Harmonic Oscillator
A force $\mathbf F$ that is proportional to the distance $\mathbf q$ from some reference position is denoted as a harmonic, or Hookian spring force, $\mathbf F = -k \: \mathbf q$ (cf Remark 3.4). One readily checks that it derives from a potential \begin{align*} V = \frac{k}{2} \: \mathbf q^2 \end{align*} such that the Lagrange function for a particle of mass $m$ takes the form \begin{align*} \mathcal L &= \frac{m}{2} \: \dot{\mathbf q}^2 - \frac{k}{2} \: \mathbf q^2 \end{align*} Accordingly, the Euler-Lagrange equations provide the EOM \begin{align} \ddot{\mathbf q} = -\frac{k}{m} \: \mathbf q \,. \tag{6.4.1} \end{align} The equation for each component can be solved independently, providing \begin{align*} q_i(t) = A_i \: \sin\bigl( \alpha_i + \omega \, t \bigr) \qquad\text{with}\quad \omega = \sqrt{ \frac{k}{m} } \, . \end{align*} Here the amplitudes $A_i$ and the phase factors $\alpha_i$ are integration constants that must be chosen in accordance with the initial condition $\bigl(\mathbf q (t_0), \dot{\mathbf q}(t_0) \bigr)$. Even though we found an explicit solution is non-trivial to sort out how the trajectories will look like. One can gain additional insight into their shape by describing the motion in terms of spherical coordinates, Theorem 6.3, \begin{align*} \mathbf q &= R(t) \, \hat{\boldsymbol R}\bigl(\theta(t), \varphi(t)\bigr) \\ \dot{\mathbf q} &= \dot R(t) \: \hat{\boldsymbol R}\bigl(\theta(t), \varphi(t)\bigr) + R(t) \: \dot\theta(t) \: \hat{\boldsymbol \theta}\bigl(\theta(t), \varphi(t)\bigr) + R(t) \: \sin\theta(t) \: \dot\varphi(t) \: \hat{\boldsymbol \varphi}\bigl(\theta(t), \varphi(t)\bigr) \end{align*} such that \begin{align*} T &= \frac{m}{2} \; \left( \dot R^2(t) + R^2(t) \: \dot\theta^2(t) + R^2(t) \: \dot\varphi^2(t)\: \sin^2\theta(t) \right) \\ V &= \frac{k}{2} \: R^2(t) \end{align*} The potential is rotationally symmetric. It depends only on $R$, and neither on $\theta$ nor on $\varphi$. Moreover, the kinetic energy also does not involve $\varphi$. Hence, $\varphi$ is cyclic. It provides the conservation law \begin{align} C_\varphi = \frac{ \partial\mathcal L}{ \partial\dot\phi } = m \: R^2 \: \sin^2\theta(t) \: \dot\varphi \tag{6.4.2} \end{align} Moreover, the Euler-Lagrange equation for $\theta$ provides \begin{align} \nonumber m \: R^2(t) \: \ddot\theta + 2\,m \: R \: \dot R \: \dot\theta &= \frac{\mathrm{d}}{\mathrm{d} t} \left( m \: R^2 \: \dot\theta \right) = \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial \dot\theta } \\ &= \frac{ \partial\mathcal L }{ \partial\theta } = m \: R^2(t) \: \dot\varphi^2(t)\: \sin\theta \: \cos\theta \tag{6.4.3} \end{align} This equation has a fixed point for $\theta = \pi/2$. We therefore choose the polar coordinates such that the initial position $\mathbf q$ and the initial velocity $\dot{\mathbf q}$ lie in the equatorial plane of the coordinate system, i.e., we require that $\theta(t_0) = \pi/2$ and that \begin{align*} 0 &= \hat{\boldsymbol \theta}\left( \frac{\pi}{2}, \varphi_0 \right) \cdot \dot{\mathbf q}(t_0) \\ &= \hat{\boldsymbol \theta}\left( \frac{\pi}{2}, \varphi_0 \right) \cdot \left[ \dot R(t_0) \: \hat{\boldsymbol R}\left( \frac{\pi}{2}, \varphi_0 \right) + R_0 \: \dot\theta(t_0) \: \hat{\boldsymbol \theta}\left( \frac{\pi}{2}, \varphi_0\right) + R_0 \: \dot\phi( t_0) \: \hat{\boldsymbol \varphi}\left(\frac{\pi}{2}, \varphi_0\right) \right] \\ &= R_0 \: \dot\theta(t_0) \\ \Rightarrow\quad& \dot\theta(t_0) = 0 \qquad\text{unless}\quad R_0 = 0 \, , \end{align*} and for for $R_0 =0$ one can still choose the coordinates such that $\dot\theta(t_0) = 0$. For this choice the angular momentum will take the constant value \begin{align*} \mathbf L = R \: \hat{\boldsymbol R} \times m\, \left( \dot R \: \hat{\boldsymbol R} + R\,\dot\varphi \:\hat{\boldsymbol \varphi} \right) = m\,R^2\: \dot\varphi \; \hat{\boldsymbol R} \times \hat{\boldsymbol \varphi} = C_\varphi \: \hat{\boldsymbol \theta} \end{align*}
Hence, Equation 6.4.3 expresses the conservation of the modulus of angular momentum, and the motion is confined to a plane due to the conservation of the direction of the angular momentum. This is in line with the analogous observation in the Kepler problem, Section 4.7.1. For $\theta=\pi/2$ and $\dot\theta=0$ the EOM for $R(t)$ takes the form \begin{align*} m \: \ddot R = \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial \dot R } = \frac{ \partial\mathcal L }{ \partial R } = m \, R \: \dot\varphi^2 - k \, R \end{align*} We employ angular-momentum conservation, $C_\varphi = m\,R^2\:\dot\varphi$, to eliminate $\dot\varphi$ in this equation. Subsequently, we introduce the dimensionless time, $\tau = \omega \, (t-t_0)$, and distance, $r = R/R_c$, based on the frequency $\omega = \sqrt{k/m}$ and the length scale $R_c = \sqrt{C_\varphi/m\,\omega}$: \begin{align} \frac{\mathrm{d}^2 r}{\mathrm{d}\tau^2} = \frac{1}{r^3} - r \tag{6.4.4} \end{align} Multiplication by $2\, \dot r$ and integration provides \begin{align*} \dot r^2(\tau) - \dot r^2(0) &= \int_0^\tau \mathrm{d}\tau \: \frac{\mathrm{d} r^2}{\mathrm{d}\tau} = -\int_0^\tau \mathrm{d}\tau \: \frac{\mathrm{d} r}{\mathrm{d}\tau} \; \frac{\mathrm{d}}{\mathrm{d} r} \left( \frac{r^2}{2} + \frac{1}{2\,r^2} \right) \\ &= -\int_{r_0}^{r(\tau)} \mathrm{d} r \; \frac{\mathrm{d}}{\mathrm{d} r} \left( \frac{r^2}{2} + \frac{1}{2\,r^2} \right) = - \left( \frac{r^2}{2} + \frac{1}{2\,r^2} \right)_{\!\! r_0}^{\!\! r(\tau)} \end{align*} This entails conservation of the dimensionless energy, \begin{align} e = \frac{\dot r^2 }{2} + \frac{r^2}{2} + \frac{1}{2\,r^2} \tag{6.4.5} \end{align} This amounts to the EOM, Equation 6.4.4, of a particle at position $r(\tau)$ that follows a dynamics with energy conservation, Equation 6.4.5, where it has a dimensionless kinetic energy $\dot r^2/2$ and a potential energy $r^2/2 + r^{-2}/2$. Hence, we refer to it as effective potential for the $r$ dynamics.
Definition 6.11 Effective potential
Let $\mathcal L( \dot q_1, \dot q_2, \cdots, q_1 )$ be a Lagrange function of a dynamics
that depends only on the velocities $\dot q_1, \dot q_2, \cdots$ and on the first coordinate $q_1$.
All other coordinates are either cyclic or fixed to specific values by other means.
Then the conservation laws resulting for the dynamics of $q_i$ with $i>1$ can be used to eliminate the velocities $\dot q_i$ for $i>1$.
This results in an EOM for $q_1(t)$ that only involves $\ddot q_1$, $\dot q_1$, $q_1$, and conserved quantities
with values fixed by initial conditions.
Often this equation can be integrated once, and cast into the dimensionless form
\begin{align*}
e = \frac{\dot \Theta^2(\tau) }{2} + \Phi_{\text{eff}}(\Theta( \tau ))
\end{align*}
where
$e$ is a constant of motion,
$\tau$ is the dimensionless time,
$\Theta$ is some function of $\dot q_1$ and $q_1$,
and $\dot \Theta$ is the $\tau$ derivative of $\Theta$.
This maps the $q_1$ dynamics to the motion of a particle with a single DOF $\Theta$,
kinetic energy $\dot \Theta^2/2$,
and an effective potential $\Phi_{\text{eff}}(\Theta)$.
Remark 6.10. If the system conserves energy, then $e$ will often amount to the non-dimensionalized energy.
Remark 6.11. In Section 6.3.2 and Section 6.3.4 we encountered settings where the angle $\varphi$ was controlled by an external motor such that the energy is not conserved (cf. Problem 6.7). In this case the constraint on $\varphi$ allows us to math the non-inertial dynamics of the rotating system into an autonomous dynamics with the effective potentials, Equation 6.3.5, Equation 6.3.7, respectively.
In the coordinate plane the trajectories of the harmonic oscillator that take the form of closed ellipses. This is most transparently confirmed by choosing the Cartesian coordinates $\mathbf q = (q_1,q_2,q_3)$ in Equation 6.4.1 such that $q_3$ vanishes and adopting a complex variable $z=q_1 + \mathrm{i}\, q_2$. The EOM will then take the form $\ddot z = -\omega^2 \, z$, and it has the general solution \begin{align*} z(t) = z_1 \: \mathrm{e}^{\mathrm{i}\,\omega (t-t_0)} + z_2 \: \mathrm{e}^{-\mathrm{i}\,\omega (t-t_0)} \end{align*} We express the complex integration constants $z_1$ and $z_2$ in terms of four real numbers $A$, $B$, $\alpha$, and $\beta$, \begin{align*} z_1 &= \frac{A+B}{2} \: \mathrm{e}^{\mathrm{i}\, (\beta+\alpha)} & z_2 &= \frac{A-B}{2} \: \mathrm{e}^{\mathrm{i}\, (\beta-\alpha)} \end{align*} and find
\begin{align} z(t) = \mathrm{e}^{\mathrm{i}\, \beta} \; \left[ A \: \cos\bigl(\alpha+\omega\, (t-t_0)\bigr) + \mathrm{i} \: B \: \sin\bigl(\alpha+\omega\, (t-t_0)\bigr) \right] \tag{6.4.6} \end{align}
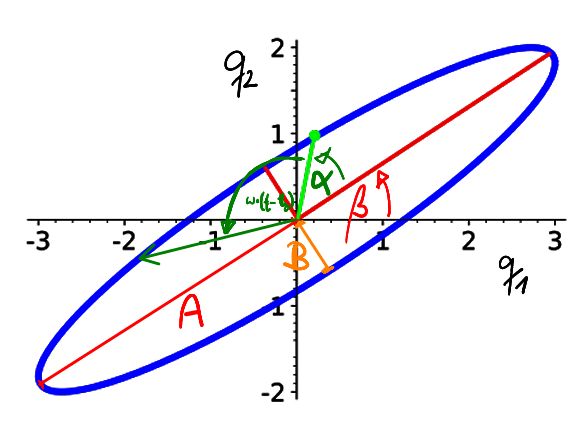
Figure 6.16: Sketch of the configuration-space trajectory of a harmonic oscillator, Equation 6.4.6.
The blue line indicates the positions visited by the trajectory.
The light green dot indicates the initial position at time $t_0$.
The dark green arrow indicates the position at some time $t$.
The particle will reside at that time at a position at a distance $\lvert z \rvert$ from the origin
with an angle $\beta+\alpha+\omega\,(t-t_0)$ with respect to the positive $q_1$ axis.
The amplitudes $A$ and $B$ describe the length of the semi-axes of the ellipse. The angle $\beta$ rotates the ellipse, i.e., it describes the orientation of the axes. The angle $\alpha$ is a phase factor that establishes the position on the ellipse where the particle started at time $t_0$. A sketch of the resulting trajectory is provided in Figure 6.16. We observe that the trajectory keeps a minimum distance $B$ to the origin. For the harmonic potential this distance can be calculated explicitly by observing that $\dot R$ vanishes at the minimum distance $R_{\text{min}}$ such that energy conservation entails
\begin{align} \nonumber E &= \frac{1}{2\,m} \: \frac{ C_\varphi^2 }{ R_{\text{min}}^2 } + \frac{k}{2} \: R_{\text{min}}^2 \\ \Rightarrow\quad R_{\text{min}}^2 &= \frac{E}{k} \; \left( 1 - \sqrt{ 1-\left( \frac{C_\varphi}{k\,E} \right)^2 } \right) \tag{6.4.7} \end{align} Hence, the trajectory can go through the origin iff $C_\varphi=0$. This observation holds for every system with energy conservation and a potential that obeys cylinder symmetry1).
Theorem 6.7 Rotation barrier
Let a particle of mass $m$ follow a dynamics
where the energy $E$ and a component $C_\varphi = \hat{\boldsymbol n} \cdot \mathbf L$ of the angular momentum $\mathbf L$ are conserved.
Then the particle will keep a minimum distance
\begin{align}
R_{\text{min}} = \frac{ \lvert C_\varphi \rvert }{ \sqrt{2m \: (E - \Phi_{\text{min}})} } \tag{6.4.8}
\end{align}
from the axis $\hat{\boldsymbol n}$.
Here, $\Phi_{\text{min}}$ is a lower bound to the potential energy.
The non-vanishing angular momentum $C_\varphi$ sets up a rotation barrier
preventing the system to enter a region close to the rotation axis.
Proof. We adopt cylinder coordinates $(R,\varphi,z)$ with a symmetry axis $\hat{\boldsymbol z}$ aligned along $\hat{\boldsymbol n}$. Then the kinetic energy and $L_n$ amount to \begin{align*} T &= \frac{m}{2} \: \left( \dot z^2 + R^2 \: \dot\varphi^2 \right) \\ C_\varphi &= m \: R^2 \: \dot\varphi \end{align*} As a consequence, we have \begin{align*} E - \varphi_{\text{min}} &\geq E - U(R, z) = T \geq \frac{m}{2} \:R^2 \: \dot\varphi^2 = \frac{C_\varphi^2}{2m\:R^2} \end{align*} The bound is obtained by solving this inequality for $R$. qed
Remark 6.12. Equation 6.4.8 implies that also in general the rotation axis can only be approached for $C_\varphi=0$.
Remark 6.13. It is not necessary that the potential $U(R, z)$ has a minimum for $R=0$. The argument works in exactly the same way when it has a maximum.2). An example is provided in Problem 6.12.
Remark 6.14. Energy conservation always provides an implicit equation for $R_{\text{min}}$. In general this equation can not be solved for $R_{\text{min}}$ such that one can only provide the inequality, Equation 6.4.8. However, besides for the harmonic potential, Equation 6.4.7, one can also explicitly determine the solution for the Kepler potential. This derivation is given as Problem 6.11.
6.4.4 Spherical pendulum
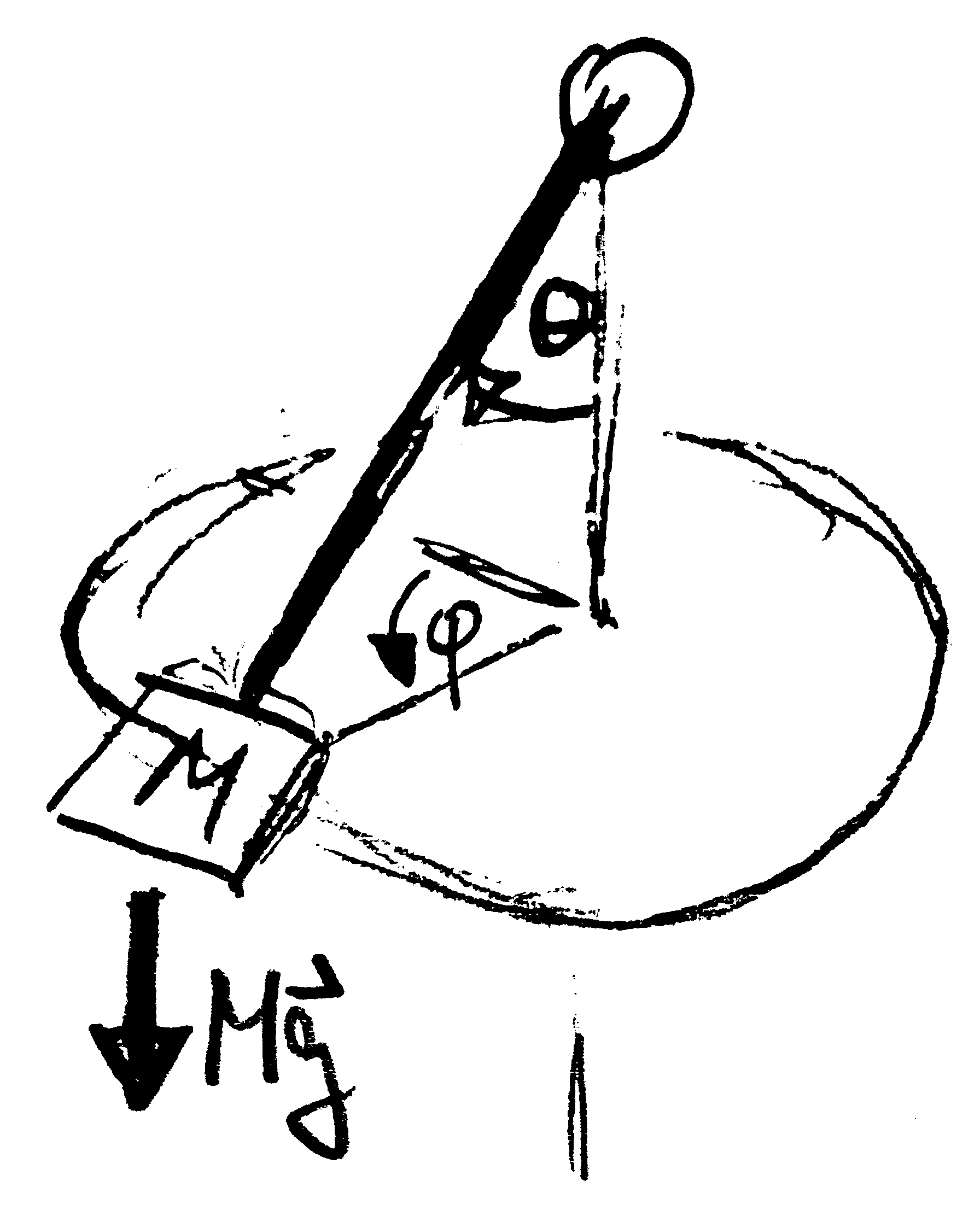
The force-free motion, free flight and harmonic oscillator all feature EOM where the motion of the different degrees of freedom were not coupled. This very exceptional. As a first step towards a more generic setting we discuss the dynamics of the spherical pendulum. The spherical pendulum describes the motion of a mass $M$ that is mounted on a bar of fixed length $\ell$ whose other end is fixed to a pivot. Thus, the position of the mass is constraint to a spherical shell. We adopt spherical coordinates to describe the position as \begin{align*} \mathbf x (t) = \ell \begin{pmatrix} \sin\theta(t) \; \cos\varphi(t) \\ \sin\theta(t) \; \sin\varphi(t) \\ -\cos\theta(t) \end{pmatrix} = \ell \, \hat{\mathbf R}\bigl(\theta(t), \varphi(t) \bigr) \\ \end{align*} Note that the angle $\theta$ is measured here with respect the negative $z$ axis, in contrast to the definition adopted in Theorem 6.3 (see Figures 6.17). As a consequence, we have now
\begin{align*} \hat{\boldsymbol\theta}(\theta,\varphi) &= \begin{pmatrix} \cos\theta \; \cos\varphi \\ \cos\theta \: \sin\varphi \\ \sin\theta \end{pmatrix} \quad\text{and}\quad \hat{\boldsymbol\varphi}(\theta,\varphi) = \begin{pmatrix}-\sin\theta \; \sin\varphi \\ \sin\theta \: \cos\varphi \\ 0 \end{pmatrix} \end{align*}
with $0 < \theta < \pi$ and $0 \leq \varphi < 2\pi$. The same rules for the derivatives apply as provided in Theorem 6.4, but now $\{ \hat{\boldsymbol R}, \hat{\boldsymbol \varphi}, \hat{\boldsymbol \theta})$ provides a right handed coordinate system, i.e., $ \hat{\boldsymbol R} \times \hat{\boldsymbol \theta} = - \hat{\boldsymbol \varphi}$. The angle $\theta$ denotes the angle between the position the mass and the gravitational field. Consequently, the potential energy in the gravitational field is obtained as \begin{align*} U = - M \: \mathbf g \cdot \mathbf x = -M\, g\, \ell\, \cos\theta(t) \, . \end{align*}
The angle $\varphi$ describes in which direction the mass is deflected from the vertical line, in a plane orthogonal to the action of gravity. For the velocity we find based on the chain rule and the derivatives of the unit vectors, Equation 6.3.3,
\begin{align*} \dot{\mathbf x} &= \ell \, \dot\theta \: \partial_\theta \hat{\mathbf R}\bigl( \theta(t), \varphi(t) \bigr) + \ell \, \dot\varphi \: \partial_\varphi \hat{\mathbf R}\bigl( \theta(t), \varphi(t) \bigr) \\ &= \ell \, \dot\theta \: \hat{\boldsymbol\theta}\bigl( \theta(t), \varphi(t) \bigr) + \ell \, \dot\varphi \: \sin\theta(t) \; \hat{\boldsymbol\varphi}\bigl( \theta(t), \varphi(t) \bigr) \end{align*} The expression for $\dot{\mathbf x}$ and the orthogonality condition $\hat{\boldsymbol \theta} \cdot \hat{\boldsymbol \varphi} = 0$ for the base vectors $\hat{\boldsymbol \theta}$ and $\hat{\boldsymbol \varphi}$ provide the kinetic energy \begin{align*} T &= \frac{M}{2} \, \dot{\mathbf x}^2 = \frac{M}{2} \, \ell^2 \, \dot\theta^2(t) + \frac{M}{2} \, \ell^2 \: \sin^2\theta(t) \: \dot\varphi^2(t) \end{align*} Consequently, the Lagrange function for the spherical pendulum takes the form \begin{align*} \mathcal L ( \theta, \varphi, \dot\theta, \dot\varphi ) = \frac{M}{2} \, \ell^2 \, \dot\theta^2 + \frac{M}{2} \, \ell^2 \: \sin^2\theta(t) \: \dot\varphi^2(t) + M\, g\, \ell\, \cos\theta(t) \end{align*} We observe that $\mathcal L$ does not depend on $\varphi$. In that case it is advisable to first discuss the EOM for $\varphi$. It takes the form \begin{align*} M \, \ell^2 \: \frac{\mathrm{d}}{\mathrm{d} t} \Bigl( \dot\varphi \: \sin^2\theta(t) \Bigr) &= \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial \mathcal L}{\partial \dot \varphi} = \frac{\partial \mathcal L}{\partial \varphi} = 0 \end{align*} The derivative of the Lagrange function with respect to $\varphi$ vanishes because $\mathcal L$ does not depend on $\varphi$. Such a coordinate is called cyclic, and it always implies a conservation law. For the spherical pendulum it entails the conservation law
\begin{align} C_\varphi = \dot\varphi \: \sin^2\theta(t) = \text{const} \tag{6.4.9} \end{align} Comparison to Equation 6.4.2 reveals $C_\varphi$ is proportional to the $z$-component of the angular momentum. The conservation law provides an expression of $\dot\varphi$ in terms of$\theta$
\begin{align} \dot \varphi(t) = \frac{C_\varphi}{\sin^2\theta(t)} \tag{6.4.10} \end{align}
Let us now consider to the other coordinate of the spherical pendulum. The EOM for $\theta(t)$ takes the form \begin{align*} M \, \ell^2 \: \ddot \theta(t) &= \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial \mathcal L}{\partial \dot \theta} \\ &= \frac{\partial \mathcal L}{\partial \theta} = M \, \ell^2 \: \dot \varphi^2(t) \; \sin\theta(t) \; \cos\theta(t) - M\, g\, \ell\, \sin\theta(t) \, . \end{align*} In this equation the unknown function $\dot\varphi(t)$ can be eliminated by means of the conservation law, Equation 6.4.9, yielding
\begin{align} \ddot \theta(t) &= \frac{ C_\varphi^2 \, \cos\theta(t) }{ \sin^3\theta(t) } -\frac{g}{\ell} \; \sin\theta(t) \tag{6.4.11} \end{align}
For $C_\varphi=0$ the particle swings in a fixed plane selected by $\varphi = \text{const}$. Its motion amounts to that of the mathematical pendulum, Equation 6.3.1. The resulting EOM can be integrated once by multiplication with$2\dot\theta(t)$
\begin{align} \dot\theta^2(t) - \dot\theta^2(t_0) &= \int_{t_0}^t \mathrm{d} t \: 2 \dot\theta \left( \frac{ C_\varphi^2 \, \cos\theta(t) }{ \sin^3\theta(t) } - \frac{g}{\ell} \; \sin\theta(t) \right) \nonumber\\ \nonumber &= -2 \; \int_{\theta(t_0)}^{\theta(t)} \mathrm{d} \theta \: \frac{\mathrm{d}}{\mathrm{d} \theta} \left( -\frac{C_\varphi^2}{\sin^2\theta} + \frac{g}{\ell} \; \cos\theta \right) \end{align} The result can be written in the form \begin{align*} E &= \frac{\dot\theta^2(t)}{2} + \Phi_{\text{eff}}\bigl(\theta(t) \bigr) = \text{const} \\ \text{where}\quad \Phi_{\text{eff}}(\theta) &= \frac{C_\varphi^2}{\sin^2\theta} - \frac{g}{\ell} \; \cos\theta \, . \end{align*} Again a closed solution for $\theta(t)$ is out of reach. However, $\Phi_{\text{eff}}(\theta) $ can serve as an effective potential for the 1DOF motion of $\theta$ with kinetic energy $\dot\theta^2/2$. This interpretation of the dynamics provides ready access to a qualitative discussion of of the solutions of the EOM based on a phase-space plot.
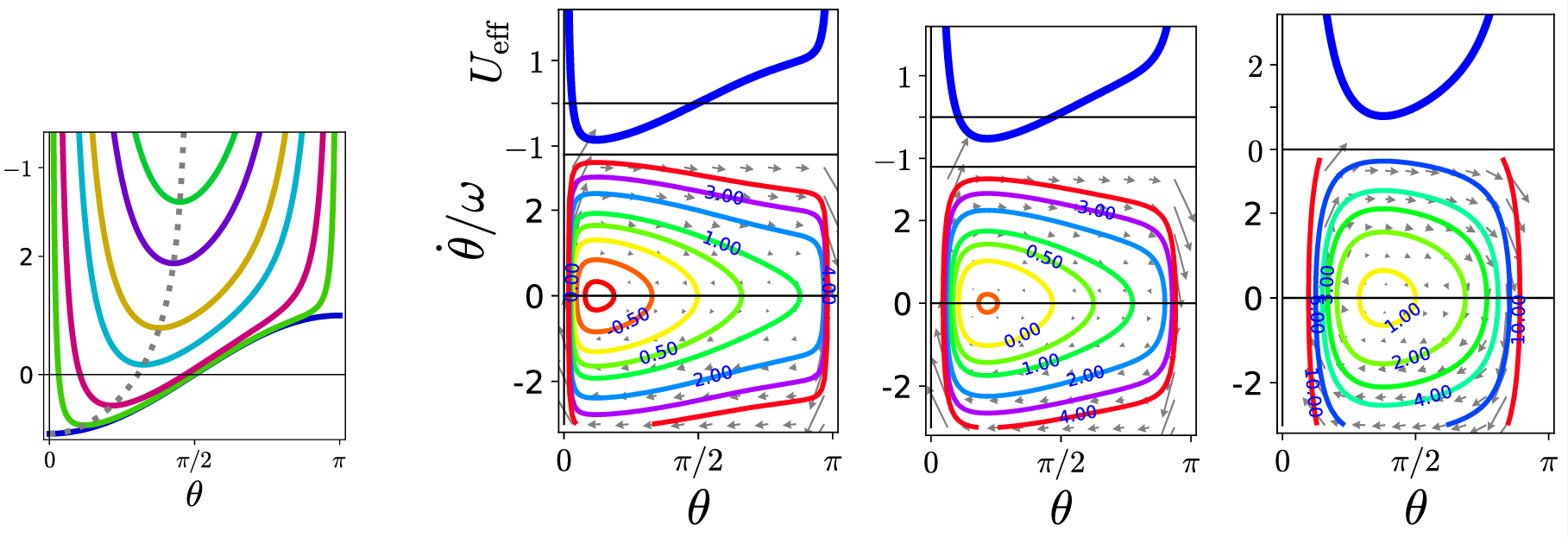
Figure 6.18: The left panel shows the effective potential for the spherical pendulum at parameter values
$C_\varphi2 \in \{ 0, 0.01, 0.1, 0.5, 1, 2, 3 \}$
from bottom to top.
The subsequent panels show phase-space portraits of the motion for $C_\varphi^2 = 0.01$, $0.1$, and$1$, respectively.
Figure 6.18 shows the effective potential and phase space portraits for different positive values of $C_\varphi$. Conservation of angular momentum implies that for $C_\varphi \neq 0$ the particle can no longer access the region close to its rest position at the lowermost point of the sphere. Rather it always has to go in circles around the bottom of the well, and the sign of $C_\varphi$ specifies whether it moves clockwise or anti-clockwise. The divergence of the effective potential at $\theta=\pm\pi$ is called rotation barrier. It emerges due to a combination of the conservation of energy and angular momentum.
The effective potential has a single minimum for $0 < \theta_c(C_\varphi) < \pi/2$, and not further extrema. The minimum describes motion where the particle moves at constant height with a constant speed in a circle. When this orbit is perturbed oscillations are superimposed on the circular motion. In a projection to the plane vertical to the action of gravity, this will lead to trajectories similar to those drawn by a Spirograph, Problem 2.42. The take-home message of this example is that cyclic variables entail conservation laws of the dynamics. In the very same manner as for the Kepler problem they can be used to eliminate a variable from the EOM of the other coordinates. The additional contributions in the EOMs for the other coordinate(s) are interpreted as part of an effective potential.
6.4.5 Self Test
Problem 6.10: Momentum conservation and free flight
We consider a system of$N$ particles with masses $m_i$.
Their interactions are translation invariant,
deriving from a potential $V(\mathbf q, t) = \sum_{i<j} \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert , t \bigr)$.
However, in addition to the setting considered in Theorem 6.6
we allow for external forces.
For each particle the force, $\mathbf F_i$, takes a constant value,
and all forces are acting in the same direction.
As an example you may consider gravity $\mathbf F_i = m_i \: \mathbf g$
or a constant electric fields $\mathbf E$ for particles with charges $e_i$.
Adapt the arguments of the proof of Theorem 6.6
to show that
- The component of the total momentum $\mathbf P$ parallel to the external forces is no longer conserved.
- All other components of the total momentum are still conserved.
- How does this finding fit with the changes of $T$ and $V$ upon translations, Problem 4.35.
Problem 6.11: Minimum distance of celestial bodies
The gravitation potential between between two celestial bodies
of masses $m$ and $M$
follows Kepler's law
\begin{align*}
U(R) = \frac{m\,M\,G}{R}
\end{align*}
It depends only on their distance $R = \lvert \mathbf R \rvert$ between the bodies.
The energy of the relative motion, Equation 4.9.1, is conserved.
- Determine the distance between the bodies upon their closest approach.
- What is the relative velocity $\lvert \dot{\mathbf R} \rvert$ of the bodies at that moment?
Problem 6.12: Evolution of a particle in a Mexican-hat potential
We explore the motion of a particle of mass $m$ in a rotation-symmetric potential
\begin{align*}
\Phi( r ) = \frac{m \, A}{4} \; r^2 \; ( r^2 - 2 \, r_0^2 )
\end{align*}
The particle evolves in a plane where its position is specified by the polar coordinates$(r, \theta)$.
a) Sketch the potential. Where are its maxima and minima?
b) Determine the Lagrange function for this problem, and determine the equations of motion for $\theta(t)$ and $r(t)$.
Bonus. The angular momentum and the energy of the particle are conserved. How do you see this without calculation based on the Lagrange function?
c) Determine a frequency $\omega$, a length scale $\ell$ and a constant $K$, such that
\begin{align*}
\frac{\mathrm{d}^2 {\hat r}}{\mathrm{d}( \omega t)^2 }
= \hat r - \hat r^3 + \frac{K}{\hat r^3}
\end{align*}
where $\hat r$ denotes the dimensionless (scalar) distance
\begin{align*}
\quad \text{with} \hat r(t) = \frac{ r(t) }{ \ell } \, .
\end{align*}
In the following we discuss the dimensionless equations,
where we absorb $\omega$ into the time scale and drop the hat to avoid clutter in the equations.
d) Multiply the equation of motion by $\dot r$, and rewrite it in the form
\begin{align*}
E = \frac{\dot{r}^2}{2} + V_{\text{eff}}(r)
\qquad
\text{ with }
\quad
V_{\text{eff}}(r) = \frac{ r^4 }{4} - \frac{ r^2 }{2} + \frac{K}{2 \, r^2} \, .
\end{align*}
e) Sketch the effective potential $ V_{\text{eff}}(r) $ and the phase portrait of the motion for $K>0$.
Bonus. Why is it necessary to give a separate discussion of $K=0$?