Table of Contents
3.3 Newton's axioms and equations of motion (EOM)
In Section 3.1 we referred to a train compartment to point out that physical observations will be the same — irrespective of the velocity of its motion, as long as it is constant. A setting where we perform an experiment is denoted as reference frame, and reference frames that move with constant velocity are called inertial systems.
Definition 3.2 Reference Frames and Inertial Systems
A reference frame $(\mathbf Q, \{\hat{\boldsymbol e}_i(t), \; i=1\cdots D\})$ is an agreement about the, in general time dependent, position of the origin $\mathbf Q(t)$ of the coordinate system and a set of orthonormal basis vectors $\{\hat{\boldsymbol e}_i(t), \; i=1\cdots D\}$, that are adopted to indicate the positions of particles in a physical model. The reference frame refers to an inertial system when it does not rotate and when it moves with a constant velocity, i.e., if and only if $\ddot{\mathbf Q} = \mathbf 0$ and $\dot{\hat{\boldsymbol e}}_i = \mathbf 0$ for all $i\in\{1\cdots D\}$.
Remark 3.1. The requirement $\dot{\hat{\boldsymbol e}}_i = \mathbf 0$ implies that the orientation of the basis vectors ${\hat{\boldsymbol e}}_i$ does not change, i.e. the reference frame does not rotate.
Remark 3.2. The rest frame for a particle is a reference frame where the particle velocity takes the constant velocity $\mathbf 0$.
Remark 3.3.
Let $\mathbf q = (q_1, \dots q_D)$ be the coordinates of a particles,
as specified in in the inertial frame $(\mathbf Q, \{ \hat{\boldsymbol e}_i \})$,
and $\mathbf x = (x_1, \dots x_D)$ its position
given in the inertial frame $(\mathbf X, \{ \hat{\boldsymbol n}_i \})$.
Then
\begin{align*}
\mathbf q = \mathbf Q + \sum_{i=1}^D q_i \, \hat{\boldsymbol e}_i
= \mathbf X + \sum_{i=1}^D x_i \, \hat{\boldsymbol n}_i \, .
\end{align*}
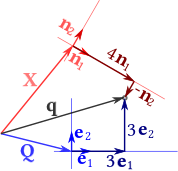Figure 3.1: Graphical illustration of the description of a position from the perspective of two different reference frames,
$\mathbf q = \mathbf Q + 3 \, \hat{\boldsymbol e}_1 + 3 \, \hat{\boldsymbol e}_2$
$= \mathbf X + 4 \, \hat{\boldsymbol n}_1 - \hat{\boldsymbol n}_2$
with the notations of Remark 3.3.
3.3.1 1st Law
As long as a reference frame moves with a constant velocity, it feels like at rest. Physical measurements can only detect acceleration. This is expressed by
Axiom 3.1: Newton's 1st law
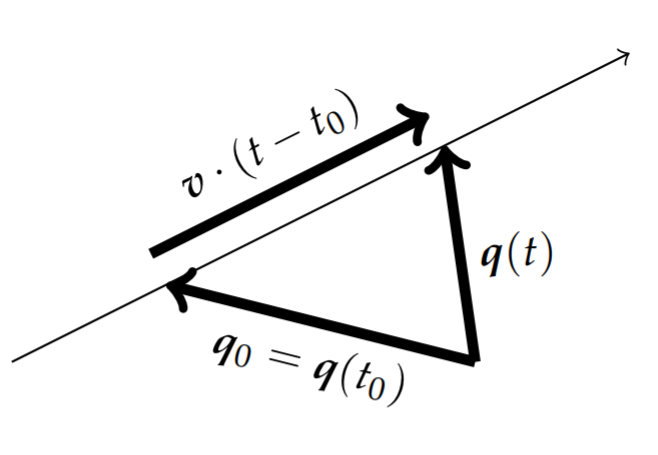
The velocity of a particle moving in an inertial system is constant, unless a (net) force is acting on the particle, \begin{align*} \forall t \geq t_0 : \mathbf F (t) = \mathbf 0 &\quad \Leftrightarrow \quad \dot{\mathbf q}(t) = \mathbf v = \text{const} \\ &\quad \Leftrightarrow \quad \mathbf q (t) = \mathbf q_0 + \mathbf v \: ( t - t_0 ) \\ \end{align*} as sketched in the margin.
The particle moves then in a straight line with a constant speed. Indeed, when a particle moves with the constant velocity $\mathbf v = \dot{\mathbf q}(t)$ in the reference frame $(\mathbf Q_1, \{\hat{\boldsymbol e}_i(t), i=1\cdots D\}$ then it is at rest in the alternative reference frame $(\mathbf Q_2, \{\hat{\boldsymbol e}_i(t), i=1\cdots D\}$ where $\mathbf Q_2 = \mathbf Q_1 + \mathbf v \: t$. Therefore, in the latter coordinate system the particle is at rest, and it will remain at rest when it is not perturbed by a net external force. After all, \begin{align*} \mathbf q = \mathbf Q_1 + \mathbf v \, t = \mathbf Q_2 + \mathbf 0 \, . \end{align*}
3.3.2 2nd Law
Newton's second law spells out how the velocity of the particle changes when there is a force.
Axiom 3.2: Newton's 2nd law
The change, $\ddot{\mathbf q}(t)$, of the velocity of a particle, $\dot{\mathbf q}(t)$, at position, $\mathbf q (t)$, is proportional to the sum of the forces $\mathbf F_\alpha$ acting on the particle, and the proportionality factor is the particle mass $m$, \begin{align*} m \; \ddot{\mathbf q}(t) = \sum_\alpha \mathbf F_\alpha( t ) \, . \end{align*}
Remark 3.4.
In general the time dependence of the forces can be decomposed into three contributions
a) An implicit time dependence, $\mathbf F( \mathbf q(t) )$,
when the force depends on the position, $\mathbf q(t)$ of the particle.
For instance, for a Hookian spring with spring constant $k$ one has,
$\mathbf F( \mathbf q ) = - k \; \mathbf q$. 1)
b) An implicit time dependence, $\mathbf F( \dot{\mathbf q} (t) )$,
when the force depends on the velocity, $\dot{\mathbf q} (t)$ of the particle. For instance, the sliding friction for a particle with mass $m$ and friction coefficient $\gamma$
is, $\mathbf F( \dot{\mathbf q} ) = - m \, \gamma \; \dot{\mathbf q}$.
c) An explicit time dependence when the force is changing in time.
For instance, when pushing a child sitting on a swing one will only push when the swing is moving in forward direction.
Typically, one explicitly sorts out these dependencies and writes
\begin{align*}
m \, \ddot{\mathbf q}(t) = \sum_\alpha \mathbf F_\alpha( \mathbf q(t), \dot{\mathbf q} (t), t )
\end{align*}
The resulting relation between the acceleration and the force is called equation of motion of the particle.
Definition 3.3 Equation of Motion (E.O.M.)
Newton's second law establishes a relation between
the position $\mathbf q(t)$ of a particle of mass $m$,
its velocity $\dot{\mathbf q}(t)$, and
acceleration $\ddot{\mathbf q}(t)$,
\begin{align*}
m \, \ddot{\mathbf q}(t) = \mathbf F( \dot{\mathbf q}(t), \mathbf q(t), t )
\\
\end{align*}
that is referred to as the equation of motion (E.O.M.) of the particle.
The motion of $N$ particles
residing at the positions $\mathbf q_1(t), \dots, \mathbf q_N(t) \in \mathbb{R}^D$
and interacting with each other
amounts to $N\,D$ coupled equations
\begin{align*}
m \, \ddot{\mathbf q}_1 (t)
&= \mathbf F_1\bigl( \dot{\mathbf q}_1(t),\dots,\dot{\mathbf q}_N(t), \mathbf q_1(t), \dots, \mathbf q_N(t), t \bigr)
\\
\vdots \qquad & \quad \vdots
\\
m \, \ddot{\mathbf q}_N (t)
&= \mathbf F_N\bigl( \dot{\mathbf q}_1(t),\dots,\dot{\mathbf q}_N(t), \mathbf q_1(t), \dots, \mathbf q_N(t), t \bigr)
\\
\end{align*}
The primary aim of Theoretical Mechanics is to determine the solution of the E.O.M. for given initial conditions (cf. Definition 1.6), \begin{align*} \Gamma_0 = \Bigl( \mathbf q_1(t_0), \dots, \mathbf q_N(t_0), \dot{\mathbf q}_1(t_0),\dots,\dot{\mathbf q}_N(t_0) \Bigr) \end{align*} for the positions and velocities of the particles at time $t_0$. Bundles of phase-space trajectories characterize the motion of sets of trajectories, and they can be analyzed to determine how the behavior of a system changes upon varying the parameters of the setup.
Example 3.1: Particle moving in the gravitational field
The gravitational field induces a constant force $m\, \mathbf g$ on a particle with mass $m$. Let it have velocity $\mathbf v_0$ at time $t_0$ when it is taking off from the position $\mathbf q_0$. Then Newton's 2nd law states that $\ddot{\mathbf q} (t) = \mathbf g$, and this equation must be solved subject to the initial conditions $\mathbf q( t_0 ) = \mathbf q_0$ and $\dot{\mathbf q}(t_0) = \mathbf v$. By working out the derivatives one readily checks that this is given for \begin{align*} \mathbf q (t) = \mathbf q_0 + \mathbf v \; ( t - t_0) + \frac{1}{2} \; \mathbf g \; ( t - t_0)^2 \end{align*}
Example 3.2 Particle moving in a circle
Let a particle of mass $m$ move with constant speed in a circle of radius $R$
such that its position can be written as
\begin{align*}
\mathbf q (t) =
\begin{pmatrix}
R \; \cos( \omega t ) \\
R \: \sin( \omega t )
\end{pmatrix}
\end{align*}
with a constant angular velocity $\omega$.
Then its velocity and acceleration take the form
\begin{align*}
\dot{\mathbf q} (t) &=
\begin{pmatrix}
-\omega \, R \; \sin( \omega t ) \\
\omega \, R \: \cos( \omega t )
\end{pmatrix}
\\
\text{and}
\quad
\ddot{\mathbf q} (t) &=
\begin{pmatrix}
-\omega^2 \, R \; \cos( \omega t ) \\
-\omega^2 \, R \: \sin( \omega t )
\end{pmatrix}
= -\omega^2 \: \mathbf q(t)
\end{align*}
The speed is constant, taking the value $\sqrt{ \dot{\mathbf q} \cdot \dot{\mathbf q} } = \omega \, R$. The force is antiparallel to $\mathbf q$ with magnitude $m\, \omega^2 \, R$. Moreover, $\dot{\mathbf q} \cdot \mathbf F = 0$ at all times. Hence, the force only changes the direction of motion, and not the speed.
3.3.3 3rd Law
Newton's third law states that the reference frame does not matter for the description of the evolution of two particles, even when they interact with each other — i.e. when they exert forces on each other. Consider for instance the motion of two particles of the same mass $m$ that reside at the positions $\mathbf q_1(t)$ and $\mathbf q_2(t)$. We decide to observe them from a position right in the middle between the two particles $\mathbf Q = \bigl( \mathbf q_1(t) + \mathbf q_2(t) \bigr)/2$. In the absence of external forces this is an inertial frame, such that $\ddot{\mathbf Q} = \mathbf 0$ according to Newton's first law. However, Newton's second law implies that also \begin{align*} \mathbf 0 = 2m \ddot Q = m \, \ddot{\mathbf q}_1 + m \, \ddot{\mathbf q}_2 = \mathbf F_1 + \mathbf F_2 \end{align*} where $\mathbf F_1 = m\, \ddot{\mathbf q}_1$ and $\mathbf F_2 = m\, \ddot{\mathbf q}_2$ are the forces acting on particle $1$ and $2$, respectively. Up to a change of sign the forces are the same, $\mathbf F_1 = - \mathbf F_2$. This action-reaction principle is stipulated by
Axiom 3.3: Newton's 3rd law
Forces act in pairs:
- actio when a body $A$ is pushing a body $B$ with force $\mathbf F_{A \rightarrow B}$
- reactio then $B$ is pushing $A$ with force $\mathbf F_{B \rightarrow A} = - \mathbf F_{A \rightarrow B}$
- and these forces are always balanced, $\mathbf F_{A \rightarrow B} + \mathbf F_{B \rightarrow A} = \mathbf 0$.
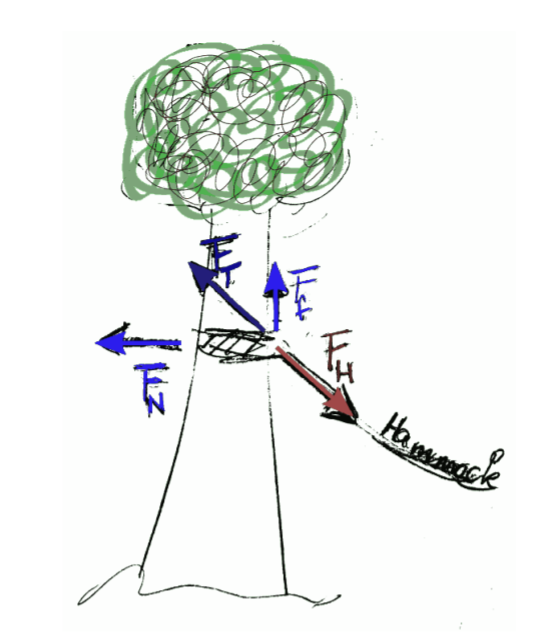Figure 3.2: Graphical illustrations of forces involved in hanging a hammock on a tree, Example 3.3
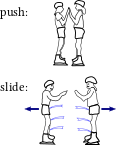Figure 3.3: Graphical illustrations of motion of the two ice-skaters of Example 3.4.
Michal Richard Trowbridge / wikimedia, CC BY-SA 3.0
Figure 3.4: Launching a water rocket, as introduced in Example 3.5.
Example 3.3 Fixing a hammock at a tree
When you lie in a hammock that is fixed at a tree, your hammock exerts a force $\mathbf F_H$ on the tree (actio). The hammock stays where it is because the tree pulls back with exactly the same force $-\mathbf F_T$, up to a change of sign (reactio), and, in turn, this force can be written as the sum of two components accounting for the normal force $F_N$ of the tree on the rope and a friction force $F_f$ that prevents the rope from sliding down the tree.
Example 3.4 Ice skaters
- When two ice skaters of the same mass push each other starting from a position at rest, then they will move in opposite directions with the same speed (unless they brake).
- When they have masses $m_1$ and $m_2$ their velocities will be related by $m_1 \, \mathbf v_1 + m_2 \, \mathbf v_2 = \mathbf 0$ because $\mathbf v_1 = \mathbf v_2 = \mathbf 0$ initially, and $m_1 \, \dot{\mathbf v}_1 + m_2 \, \dot{\mathbf v}_2 = \mathbf F_1 + \mathbf F_2 = \mathbf 0$ at any instant of time. As long as they push, the velocities are non-zero and speed increases. When they slide there is no force any longer, and they go at constant speed—except for the impact of friction of the skates on the ice.
Example 3.5 Water Rocket
A water rocket receives its thrust by the repulsive force in response of accelerating and releasing a water jet.
Let $M$ the mass of a rocket at a given time, and $V_R$ its speed.
To determine the acceleration of the rocket
we consider a short time interval $\Delta t$ where water of mass $\Delta M$ is ejected with speed $v_f$.
In the absence of gravitation the momentum balance implies
that at any given time the momentum of the rocket $M(t) \, V_R(t)$ must amount to the sum
of the water $\Delta M \: (v_R(t) - v_f)$ emitted during a short time $\Delta t$
and the momentum of the rocket $M(t+\Delta t) \, V_R(t+\Delta t)$
after that time,
\begin{align*}
M \, V_R &= (M-\Delta M) \, (V_R + \Delta V_R) + \Delta M \, (V_R - v_f)
\\
\Leftrightarrow\qquad
0 &= M \: \Delta V_R - \Delta M \: v_f - \Delta M \: \Delta V_R
\end{align*}
Now we observe that $\Delta M = a\,\rho, v_f \, \Delta t$
where $a$ is the cross
section of the ejected jet, and
$\rho$ the mass density of the ejected water:
\begin{align*}
M \: \frac{\Delta V_R}{\Delta t}
= a\,\rho, v_f^2
+ a\,\rho, v_f \; \frac{\Delta V_R}{\Delta t} \: \Delta t
\end{align*}
and in the limit of small time increments $\Delta t \to 0$ we obtain
the force $F_R$ that is accelerating the rocket
\begin{align*}
F_R = M\, \dot V_R = a\,\rho \, v_f^2
\end{align*}
The rocket trajectory results from interplay of gravity and$F_R$.
One case will be discussed as worked example at the end of this chapter,
in Section 3.5.
Solving the general case has been suggested as an instructive computer-based example for teaching mechanics (Gale, 1970; Finney, 2000).
Instructions about how to build and discuss the rocket in school is available from the
NASA and the
instructables community.
3.3.4 Punchline
Newton's equations are stated nowadays in terms of derivatives, a concept in calculus that has been pioneered by Leibniz2). In this language they take the following form for a particle of mass $m$ that is at position $\mathbf q(t)$ at time $t$, \begin{align*} \dot{\mathbf q} (t) &= \mathbf v(t) \\ \dot{\mathbf v} (t) &= \frac{1}{m} \; \mathbf F_{\text{tot}} ( \mathbf q(t), \mathbf v(t), t ) \end{align*} Prior to Newton, physical theories adopted the Aristotelian point of view that $\mathbf v$ is proportional to the force. Indeed in those days many scientists were regularly inspecting mines, and from the perspective of pushing mine carts is is quite natural to assert that their velocity is proportional to the pushing force. Galileo's achievement is to add the `tot' of the force side of the equation, pointing out that there also is a friction force acting on the mine cart. Newton's achievement is to add the `dot' on the left side of the equation, stating that the velocity stays constant when the pushing force and the friction force balance.
Example 3.6 Pushing a mine cart
The motion of the mine cart is one-dimensional along its track such that the position, $q$, velocity, $x$, and forces are one-dimensional, i.e., scalar functions.
Once the mine cart is moving it experiences a friction force $\mathbf F_f = -\gamma \, \mathbf v$,
that (to a first approximation) is proportional to its velocity, $\mathbf v$.
Now, let the mine worker push with a constant force $F_M$ such that
\begin{align*}
m\, \ddot q = m\, \dot v = F_{\text{tot}} = F_M - \gamma \, v \, .
\end{align*}
The mine cart travels with constant velocity $\dot v = 0$, when the attacking forces balance,
i.e., for $v_c = F_M / \gamma$.
For a different initial velocity, $v(t_0) = v_0$, one finds an exponential approach to the asymptotic velocity,
\begin{align*}
v (t) = v_c + \bigl( v_0 - v_c \bigr) \; \mathrm{e}^{ - \gamma \, (t-t_0) / m }
\end{align*}
After all,
$v(t_0) = v_c + \bigl( v_0 - v_c \bigr) = v_0$
and
\begin{align*}
m \: \dot v (t)
&= \bigl( v_0 - v_c \bigr) \; (-\gamma) \, \mathrm{e}^{ - \gamma \, (t-t_0)/m }
\\
&= -\gamma \; \bigl( v(t) - v_c \bigr) = -\gamma \; v(t) + F_M
\end{align*}
Figure 3.5: The pre-Newtonian understanding of the relation between force and velocity of a body.
The advantage of the Newtonian approach above earlier modeling attempts is that it makes a quantitative prediction about the asymptotic velocity, and that it also addresses the regime where the velocity is changing, e.g., when the mine cart is taking up speed.
3.3.5 Self Test
Problem 3.3: Terminal velocity for turbulent drag
Rather than a friction of the type of the mine cart,
a golf ball experiences a drag force
\begin{align*}
\mathbf F_d = -\frac{\rho |u|^2}{2} c_d A \: \hat{\boldsymbol u}
\end{align*}
where $A$ is the cross section of the ball,
$\rho$ the density of air,
$\mathbf u$ the velocity of the golf ball,
and $c_d \simeq 0.5$ the drag coefficient.
- The drag coefficient is a dimensionless number that depends on the shape of the object that experiences drag. For the rest the expression for the drag force follows from dimensional analysis. Verify this claim.
- A slightly more informed derivation of $\mathbf F_d$ introduces also the diameter $D$ of the golf ball and states that drag arises because the ball has to push air out of its way. When moving it has to push air out of the way at a rate $A\, u$. The air was at rest initially and must move roughly with a velocity $u$ to get out of the way. Subsequently, its kinetic energy is lost. Check out, how this leads to the expression provided for $\mathbf F_d$.
- What is the terminal velocity of a golf ball that is falling out of the pocket of a careless hang glider?
- Use dimensional analysis to estimate the distance after which the ball acquires its terminal velocity, and how long it takes to reach the velocity.
Problem 3.4: Orbit of the Moon around Earth
The Moon is circling around Earth due to the gravitational force of modulus
\begin{align*}
F_{ME} = \frac{G M_E M_M}{R_{ME}^2}
\end{align*}
where $G = \frac{2}{3} \times 10^{-12} \, \text{m$^3$/kg s}$
is the gravitational constant,
$M_E \simeq 6 \times 10^{24}\, \, \text{kg}$ and
$M_M \simeq \frac{3}{4} \times 10^{-23} \, \text{kg}$
are the masses of Moon and Earth, respectively,
and $R_{ME} = \frac{7}{4} \times 10^6 \, \text{m}$
is the distance from Earth to Moon.
- Calculate the force that Moon is experiencing due to the Earth. Compare it to the gravitational acceleration $g \simeq 10 \, \text{m/s$^2$}$ scaled by $(R_{ME}/R_E)^2$ where $R_E = 2\pi\times 10^6 \, \text{m}$ is the Earth radius. Why would one scale by this factor?
- Assume that the Moon trajectory is circular and identify $F_{ME}$ with the centripetal force that keeps the moon on its orbit. What does this tell about the dependence of the period $T$ of the motion on $G$, $R_{ME}$ and the masses.
- Evaluate $T$ and compare it to the duration of a month.
Problem 3.5: Escape velocities
The escape velocity is the minimum speed of a projectile
that would allow it to escape into outer space
when friction due to the atmosphere is neglected.
- Estimate the escape velocity of Earth based on the gravitational force law $F_{ME}$ given in Problem 3.4, the gravitational acceleration $g=10 \, \text{m/s$^2$}$ on Earth, and the fact that the Earth circumference was set to $2\pi R_E = 4 \times 10^{4}\, \, \text{km}$.
- Recall the relation between gravity on Earth and Moon given in Problem 1.8, and estimate also the escape velocity from Moon.
- After you performed the calculations: Compare your estimates to the values provided by Wikipedia.
Problem 3.6:
Pulling a cow
A child is pulling a toy cow with a force of $F = 5 \, \text{N}$. The cow has a mass of $m = 100 \, \text{g}$
and the chord has an angle $\theta=\pi/5$ with the horizontal.3)
- Describe the motion of the cow when there is no friction. In the beginning the cow is at rest.
- What changes when there is friction with a friction coefficient of $\gamma = 0.2$, i.e. a horizontal friction force of magnitude $-\gamma m g$ acting on the cow.
- A more informed choice for the friction $\gamma N$ takes into account that the normal force $N$ on the surface is reduced to a smaller value than $mg$ when the cow is pulled. How will that change the discussion?
- Is the assumption realistic that the force remains constant and will always act in the same direction? What might go wrong?