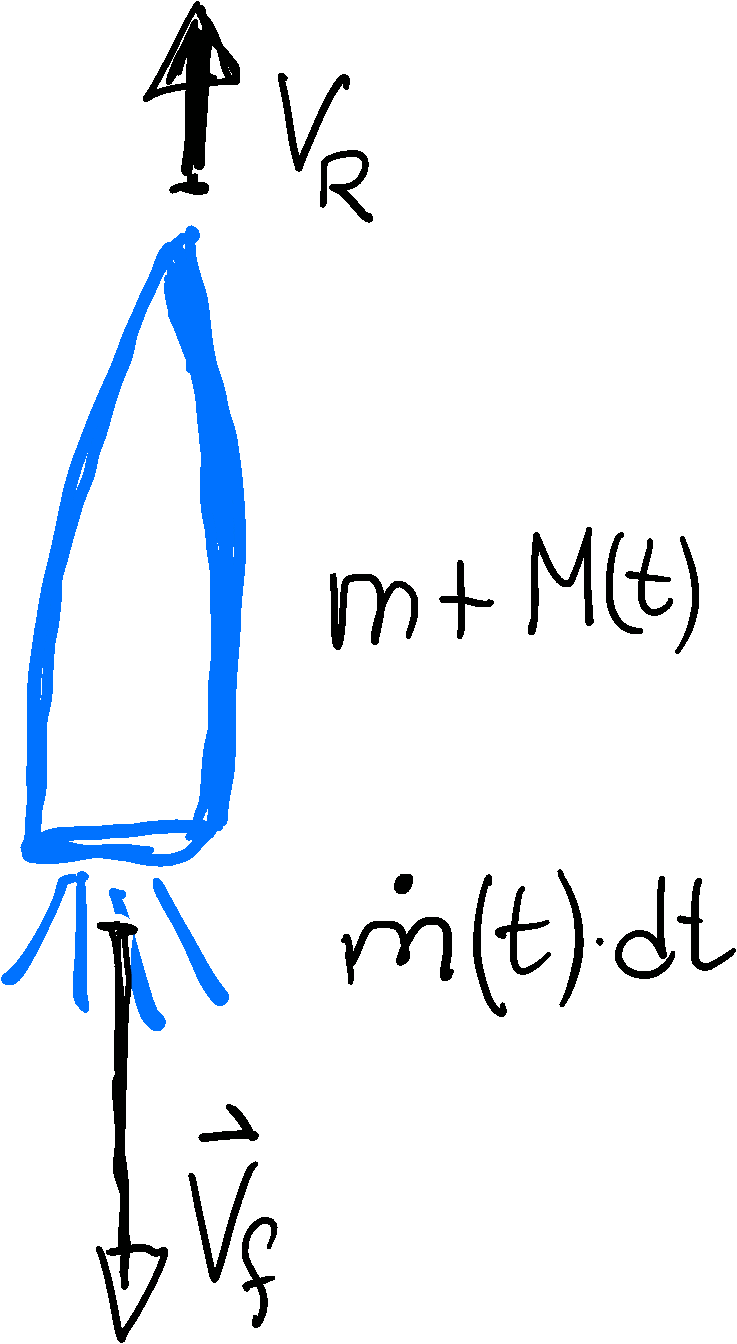3.5 Worked example: Flight of an Earth-bound rocket
In order to illustrate the applications of Newton's laws we discuss now the flight of a rocket. We will deal with the case a) where the rocket is moving in vertical direction, b) where the fuel is ejected with a constant speed $v_f$ (or zero when it is exhausted), and c) where the rocket does not reach heights with a noticeable change of the gravitational acceleration. At the end of this section we discuss the impact of relaxing these assumptions, and point to the literature for a further discussion. Let $V_R$ be the speed of the rocket. It is positive when the rocket goes up, and negative when it falls down. On the way down, its mass will be $m$. Initially, it has a mass $m+M_0$, where $M_0$ is mass of the fuel (cf Figure 3.9). As long as the rocket is firing, Newton's third law implies that
\begin{align*} F_R = \bigl( m+M(t) \bigr) \: \dot V_R = a \, \rho \, v_f^2 - \bigl( m+M(t) \bigr) \: g \end{align*}
The first force on the right-hand side of this equation accounts for the recoil from ejection of the fuel (cf Example 3.5) and the latter to gravitational acceleration. We also observed in Example 3.5 that the mass $M(t)$ of the remaining fuel at time $t$ obeys the differential equation $\dot M = -a \, \rho \, v_f$ such that 1)
\begin{align*} M(t) = M_0 - a \, \rho \, v_f \, t \, . \end{align*} At some time $T$ all fuel is consumed, and we have \begin{align*} 0 = M_0 - a \, \rho \, v_f \, T \quad\Rightarrow\quad T = \frac{M_0}{a \, \rho \, v_f} \, . \end{align*} Moreover, for the rocket acceleration we find \begin{align}\nonumber \dot V_R(t) = \frac{F_R}{ m + M(t) } = -g + \frac{ v_f/T }{ \mu - t/T } \quad\text{with}\quad \mu = \frac{ m+M_0 }{ M_0 } \end{align} The rocket speed is obtained by integrating the acceleration from the initial time, where the rocket is at rest, till time $t$. The integral takes a simpler form when one adopts the dimensionless integration variable, $\tau = t/\mu T$,
\begin{align} V_R(t) &= \mu T \: \int_0^{t/\mu T} \mathrm{d}\tau \: V_R(t) = -g\,t - v_f \: \int_0^{t/\mu T} \mathrm{d}\tau \: \frac{1}{1-\tau} \nonumber \\ &= -g\,t - v_f \: \ln\left( 1 - \frac{t}{\mu T} \right) \tag{3.5.1a} \end{align}
Thus, at time $T$ the rocket has acquired the speed
\begin{align} V_R(T) = -g \, T + v_f \, \ln\frac{ \mu - 1 }{\mu} \tag{3.5.1b} \, . \end{align}
The rocket height $z(t)$ is obtained by observing that $\dot z(t) = V_R(t)$, which in turn is given by Equation 3.5.1a. The solution where the rocket starts at height zero is the given by
\begin{align} z(t) &= \mu T \: \int_0^{t/\mu T} \mathrm{d}\tau \: V_R(t) = - \frac{g \, t^2}{2} - \mu T \, v_f \; \int_0^{t/\mu T} \mathrm{d}\tau \: \ln( 1-\tau ) \nonumber \\ &= - \frac{g \, t^2}{2} - \mu T \, v_f \; \left[ (\tau-1) \; \bigl( -1 + \ln( 1-\tau ) \bigr) \right]_0^{t/\mu T} \nonumber \\ &= - \frac{g \, t^2}{2} + v_f \,t + v_f \, T\: \left( \mu - \frac{t}{T} \right) \; \ln\left( 1 - \frac{ t }{\mu T} \right) \, . \tag{3.5.2a} \end{align}
At time $T$ this simplifies to
\begin{align} z(T) &= - \frac{g \, T^2}{2} + v_f\,T \; \left[ 1 + (\mu-1) \: \ln\frac{\mu-1}{\mu} \right] \tag{3.5.2b} \end{align}
Starting from that position the rocket will perform a ballistic flight with initial velocity $V_R(T)$ that will add to its height another height increment of $V_R^2(T)/2g$. The additional height increment $\Delta H$ before the rocket reaches the crest of its height is found by energy conservation and Equation 3.5.1b.
\begin{align} m \, g \: \Delta H &= \frac{m}{2} \: V_R^2(T) \nonumber\\ \Rightarrow \quad \Delta H &= \frac{ V_R^2(T) }{2 \, g} = \left[ \frac{g\,T^2}{2} - T \: v_f\: \ln\frac{ \mu - 1 }{\mu} + \frac{v_f^2}{2\, g} \: \left(\ln\frac{ \mu - 1 }{\mu} \right)^2 \right] \tag{3.5.3} \end{align}
Combining Equation 3.5.2b and Equation 3.5.3 yields the total height, $H$, reached by the rocket,
\begin{align}\nonumber H &= z(T) + \Delta H = \left[ - \frac{g \, T^2}{2} + v_f \, T + (\mu-1) \,v_f \, T \; \ln\frac{\mu-1}{\mu} \right] \\ \nonumber &\quad + \left[ \frac{g \, T^2}{2} + v_f \, T \: \ln\frac{\mu-1}{\mu} + \frac{v_f^2}{2 \, g} \; \left( \ln\frac{\mu}{ 1 + \mu } \right)^2 \right] \\ &= v_f\, T \; \left[ 1 + \mu \: \ln\frac{\mu-1}{ \mu } \right] + \frac{v_f^2}{2 \, g} \; \left( \ln\frac{\mu-1}{ \mu } \right)^2 \tag{3.5.4} \end{align}
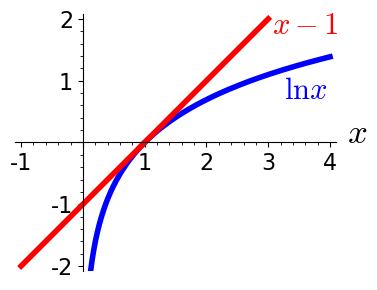
For $m>0$ we have $\mu > 1$, and the expression in the square bracket is always negative, as one can see based on the inequality $\ln x \leq x-1$ shown Figure 3.10, \begin{align*} 1 + \mu \: \ln(1+\mu^{-1}) &\leq 1 + \mu \; \left( 1 + \mu^{-1} - 1 \right) = 0 \end{align*} The best strategy to achieve a large height is to go for a small $T$ in order to suppress the first term in Equation 3.5.4 and large $v_f$ to achieve large values of the second term. When energy efficiency is a concern, e.g., when the rocket is used for a measurement of the atmosphere at height $H$, one might be interested to reach the height $H$ with minimum energy cost. This means one is interested to minimize the ratio of the potential energy of the rocket at height $H$ and the the energy $M_0 v_f^2/2$ burned to deliver the freight,
\begin{align} \eta = \frac{m \, g\, H}{M_0 v_f^2/2} &= \frac{2\, m\, g\, T}{M_0 \, v_f} \; \left[ 1 + \mu \: \ln\frac{\mu-1}{ \mu } \right] + \frac{m}{M_0} \; \left( \ln\frac{\mu}{ 1 + \mu } \right)^2 \nonumber\\ &= \frac{2\, g\, T}{v_f} \; (\mu-1) \, \left[ 1 + \mu \: \ln\frac{\mu-1}{ \mu } \right] + (\mu-1) \; \left( \ln\frac{\mu-1}{ \mu } \right)^2 \tag{3.5.5} \end{align}
The efficiency is a function of $\mu$ and of the dimensionless number $\alpha=g\,T/v_f$. The contour lines of $\eta(\mu,\alpha)$ are plotted in the left panel of Figure 3.11.
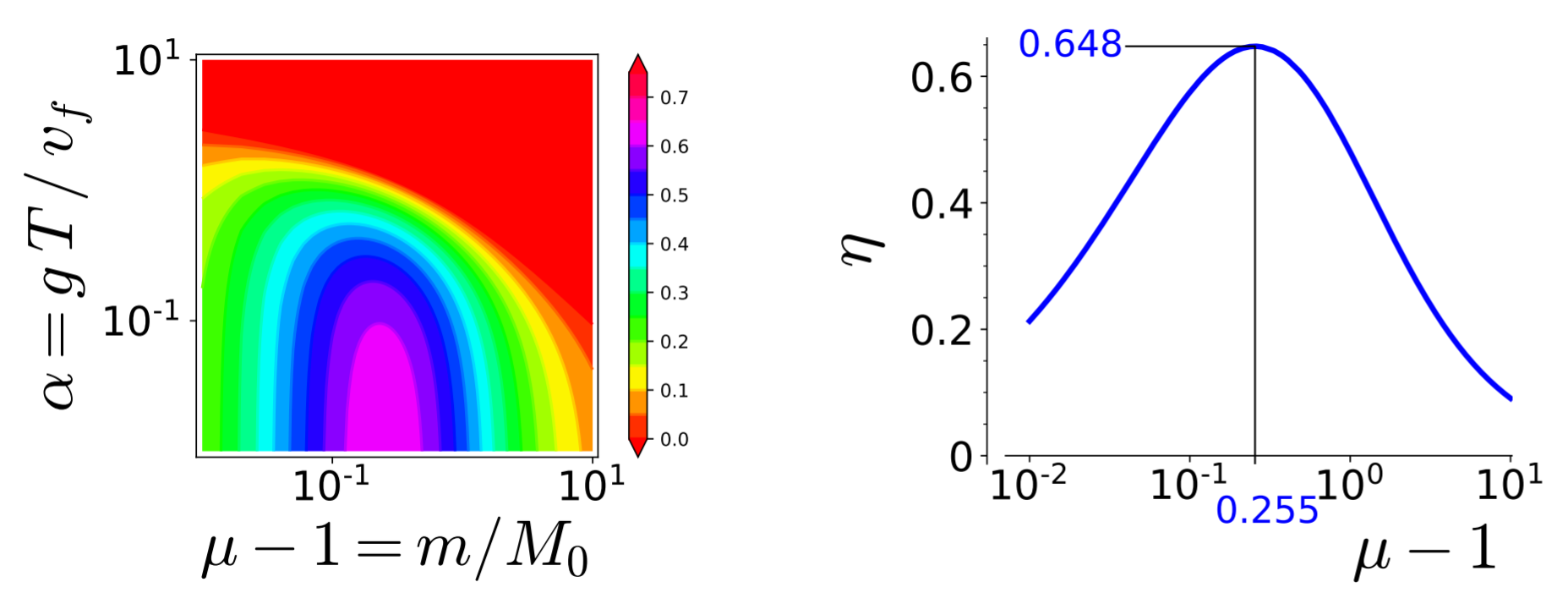 Figure 3.11: (left) Contour line for the efficiency, Equation 3.5.5,
as function of the mass ratio $m/M_0 = \mu-1$ and the dimensionless inverse rocket acceleration
$\alpha = gT/v_f$.
The maximum is taken for $\alpha = 0$.
(right) Plot of the $\mu$ dependence of the efficiency for $\alpha = 0$.
The maximum efficiency of $\eta_{\text{opt}}\simeq 0.648$ is obtained for $\mu_c\simeq 1.255$.
Figure 3.11: (left) Contour line for the efficiency, Equation 3.5.5,
as function of the mass ratio $m/M_0 = \mu-1$ and the dimensionless inverse rocket acceleration
$\alpha = gT/v_f$.
The maximum is taken for $\alpha = 0$.
(right) Plot of the $\mu$ dependence of the efficiency for $\alpha = 0$.
The maximum efficiency of $\eta_{\text{opt}}\simeq 0.648$ is obtained for $\mu_c\simeq 1.255$.
Definition 3.7 Contour lines and isosurfaces
The contour lines of a two variable function $f(x,y)$ are those lines in the $(x,y)$-plane, where $f(x,y)$ takes some constant value. More generally these lines are also called isolines, the two-dimensional surfaces where a three-variable function $g(x,y,z)$ in the $(x,y,z)$-space takes constant values are called isosurfaces, and the $N-1$-dimensional hypersurfaces of $\mathbb{R}^N$ where the function $h(\mathbf q)$ with $\mathbf q \in \mathbb{R}^N$ takes a constant values will also be denoted as isosurfaces.
Example 3.14 Isosurfaces of the 3D Gaussian distribution
The 3D Gaussian distribution \begin{align*} P(x,y,z) = \frac{1}{(2\pi D\, t)^{3/2}} \: \exp\left(- \frac{x^2 + y^2 + z^2}{2Dt} \right) \end{align*} describes the distribution of dye molecules at time $t$ when a tiny droplet of dye is added without motion in a large container of water (Brownian motion). At any given instant of time the surfaces where the concentration take constant values $C$ amount to \begin{align*} & C = (2\pi D\, t)^{-3/2} \: \exp\bigl(- (x^2 + y^2 + z^2)/(2Dt) \bigr) \\ \Leftrightarrow \quad & x^2 + y^2 + z^2 = - 2Dt \: \ln\bigl( C \: (2\pi D\, t)^{3/2} \bigr) = R^2 \end{align*} where $R^2$ is an abbreviation of the (positive) constant on the right-hand side of the equation. Hence, the isosurface $I_R$ for a given $R$ amounts to a sphere of radius $R$, \begin{align*} I_R = \{ (x,y,y) \in \mathbb{R} : x^2 + y^2 + z^2 = R^2 \} \, . \end{align*}
The contour lines of the efficiency reveal that the maximum efficiency is obtained for $\alpha = 0$, which can expected since the expression in square brackets in Equation 3.5.5 is negative. From a physics perspective it means that high efficiencies require a large fuel expulsion speed $v_f$. The maximum efficiency amounts to the maximum of $\eta(\mu,\alpha=0)=\mu \; \ln^2[\mu/(1+\mu)]$, which amounts to the root $\mu_c$ of the equation $2/(1+\mu) + \ln[\mu/(1+\mu)]$. Numerically it is found to be $\mu_c\simeq 0.255$. Hence, the maximum efficiency is obtained when the mass of the fuel $M_0$ is roughly four times larger than the mass of the empty rocket. The maximum efficiency amounts then to \begin{align*} \eta_{\text{max}} = \frac{4 \, \mu_c}{(1+\mu_c)^2} \simeq 0.648 \, . \end{align*} Irrespective of the rocket design one can not transform more than $2/3$ of the energy of the fuel into potential energy of the rocket. The remaining energy is dissipated in the kinetic energy of the exhaust. Further discussion of the trajectories of rockets can be found in (Finney (2000); Gale (1970); Seifert et al. (1947)).A discussion of water rockets that addresses the change of speed $v_f$ of the ejected water was given in (Kagan et al. (1995); Gommes (2010)).