Theoretical Mechanics IPSP

The first problem tackled in theoretical mechanics was the motion of two point particles with gravitational interaction. It is formulated in terms of three laws. The second law holds for all central forces, the 3rd law is a consequence of mechanical similarity, and the 1st law is based on a solution of the EOM. We first explore the general arguments, and then illustrate their application to the Kepler problem.

Angular momentum conservation also has important consequences for the motion of two particles. The center of mass of the two particles takes the form \begin{align*} \mathbf Q = \frac{m_1}{m_1+m_2} \: (\mathbf Q + \mathbf r_1) + \frac{m_2}{m_1+m_2} \: (\mathbf Q + \mathbf r_2) = \mathbf Q + \frac{ m_1\, \mathbf r_1 + m_2\, \mathbf r_2 }{m_1+m_2} \end{align*} such that \begin{align*} m_1\, \mathbf r_1 + m_2\, \mathbf r_2 = \mathbf 0 \quad\text{and in particular}\quad \mathbf p = m_2\, \dot{\mathbf r}_2 = - m_1 \, \dot{\mathbf r}_1 \, . \end{align*} This has important consequences for the evolution of the conserved angular momentum of the relative motion \begin{align*} \mathbf L = (\mathbf r_2 - \mathbf r_1) \times \mathbf p \, . \end{align*} In view of \begin{align*} \mathbf p = m_2\,\dot{\mathbf r}_2 &= m_2 \, \dot{\mathbf q}_2 - m_2\, \dot{\mathbf Q} = \frac{m_1 m_2}{m_1+m_2} \: \frac{\mathrm{d}}{\mathrm{d} t} \bigl( \mathbf q_2 - \mathbf q_1 ) \\ &= \mu \, \dot{\mathbf R} \quad\text{ with }\quad \mu = \frac{m_1 m_2}{m_1+m_2} \quad\text{ and }\quad \mathbf R = \mathbf q_2 - \mathbf q_1 \end{align*} the angular momentum of the relative motion can be expressed in terms of the vector $\mathbf R$ connecting the two masses \begin{align*} \mathbf L = \mathbf R \times \mu \dot{\mathbf R} \end{align*} It takes the then form the angular momentum of a single particle with mass $\mu$, and this also applies for the relation between the acceleration and the force \begin{align*} \mu \ddot{\mathbf R} = m_2\,\ddot{\mathbf r}_2 = \mathbf F \, . \end{align*} Moreover, \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathbf L = \frac{\mathrm{d}}{\mathrm{d} t} \mathbf R \times \mu \dot{\mathbf R} = \mathbf R \times \mathbf F = \mathbf 0 \end{align*} for forces $\mathbf F$ acting along the line $\mathbf R$ connecting the two particles. The conservation of angular momentum has two important consequences:
1. The direction of $\mathbf L$ is fixed. As a consequence the positions and the velocities of the planet and the sun always lie in a plane that is orthogonal to $\mathbf L$, and the force $\mu \ddot{\mathbf R}$ also lies in the plane because the force is parallel to $\mathbf R$. Therefore, the motion is constrained to the plane for all times.
2. The absolute value of $\mathbf L$ is fixed, and this has a geometric interpretation that was first formulated in the context of planetary motion

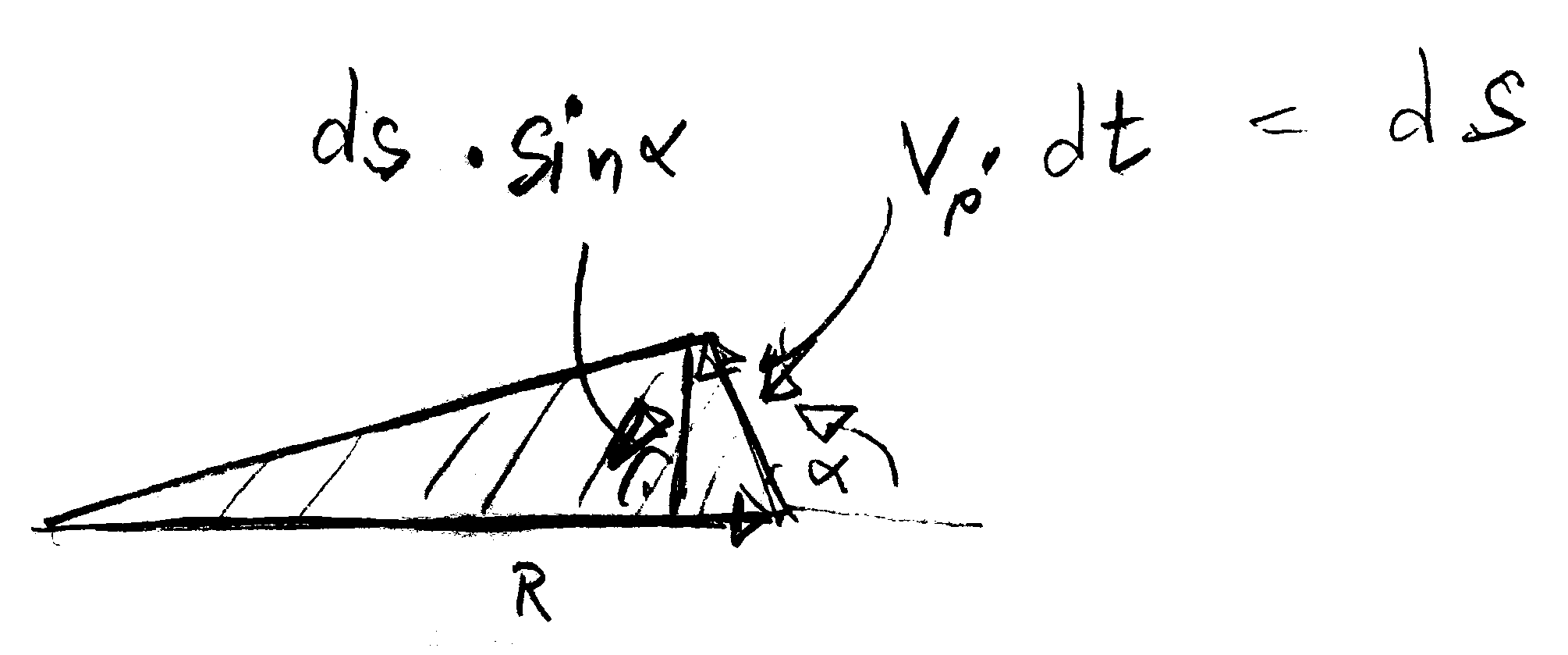
Proof. For the time interval $[t_0, t_1]$ with length $\Delta t = t_1 - t_0$ one has \begin{align*} |\mathbf L| \: \Delta t = \int_{t_0}^{t_1} \mathrm{d} t \: | \mathbf R \times (m_2 \mathbf v_2) | = m_2 \: \int_{t_0}^{t_1} \mathrm{d} t \: | \mathbf R | \: | \mathbf v_2 | \sin\alpha \end{align*} where $\alpha$ is the angle between $\mathbf R$ and $\mathbf v_2$. Further, $\mathrm{d}\mathbf s = \mathbf v_2 \, \mathrm{d} t$ is the path length that the trajectory traverses in a time unit $\mathrm{d} t$, such that $\mathrm{d} a = \mathrm{d} t \: | \mathbf R | \: | \mathbf v_2 | \sin\alpha / 2$ is the area swiped over in $\mathrm{d} t$ (see the sketch in Figure 4.13). Hence, \begin{align*} |\mathbf L| \: \Delta t = \frac{1}{2} \; \int_0^{\Delta a} \mathrm{d} a = \Delta a \quad \Rightarrow \quad \Delta a = \frac{2 \; |\mathbf L|}{m_2} \; \Delta t \end{align*} such that $\Delta a$ is proportional to $\Delta t$.
qed