Table of Contents
4.2 Integrating ODEs — Free flight
We first discuss the motion of a single particle moving in a gravitational field that gives rise to the constant gravitational acceleration$\mathbf g$. Hence, the particle position $\mathbf q(t)$ obeys the EOM
\begin{align} \ddot{\mathbf q} &= \mathbf g \tag{4.2.1} \end{align} The right hand side of this equation is constant. It neither depends on $\dot{\mathbf q}$, $\mathbf q$, nor explicitly on $t$. This has two remarkable consequences that we will exploit whenever possible.
4.2.1 Decoupling of the motion of different DOF
Each component $q_\alpha$ of $\mathbf q$ can be solved independently of the other DOF \begin{align*} \dot q_\alpha = g_\alpha \end{align*} Rather than dealing with a vector-valued ODE, one can therefore solve $D$ scalar ODEs which turns out to be a much simpler task. Indeed, we will see in our further discussion that the solution of vector-valued ODEs will often proceed via a coordinate transformation that decouples the different DOF.
4.2.2 Solving ODEs by integration
The ODE, Equation 4.2.1, can be solved by integration
Algorithm 4.1: Integrating ODEs
An ODE for $\mathbf f(t)$ can be solved by integration when its right-hand side does not depend on on $\mathbf f(t)$ and its derivatives, i.e., when it takes the form \begin{align*} \dot{\mathbf f} (t) = \mathbf g(t) \end{align*} For the initial condition $\mathbf f(t_0) = \mathbf f_0$ one can then expresses the solution of the ODE in terms of an integral,1) \begin{align*} \mathbf f (t) = \mathbf f_0 + \int_{t_0}^t \mathrm{d} t' \, \dot{\mathbf f}( t' ) = \mathbf f_0 + \int_{t_0}^t \mathrm{d} t' \, \mathbf g (t') \end{align*} For an autonomous ODE, where $\mathbf g (t) = \mathbf c = \text{const}$, one thus obtains \begin{align*} \mathbf f (t) = \mathbf f_0 + \mathbf c \cdot (t - t_0) \end{align*}
The idea underlying the algorithm can be understood by reading the equations in reverse order and taking into account the substitution rule for integration, \begin{align*} \int_{t_0}^t \mathrm{d} t' \, \mathbf g (t') = \int_{t_0}^t \mathrm{d} t' \, \dot{\mathbf f}( t' ) = \int_{f(t_0)}^{f(t)} \mathrm{d} f = f(t) - f(t_0) \end{align*}
4.2.3 Integrating the EOM for free flight
For the free flight only the constant acceleration $\mathbf g$ due to gravity is acting on the particle such that $\ddot{\mathbf q} (t) = \mathbf g$. For the initial conditions $\mathbf q(t_0) = \mathbf q_0$ and $\dot{\mathbf q}(t_0) = \mathbf v_0$. Algorithm 4.1 provides the velocity \begin{align*} \dot{\mathbf q} (t) = \mathbf v_0 + \int_{t_0}^t \mathrm{d} t' \mathbf g = \mathbf v_0 + \mathbf g \cdot (t - t_0) \end{align*} This equation can be integrated again, providing the position of the particle \begin{align*} \mathbf q (t) &= \mathbf q_0 + \int_{t_0}^t \mathrm{d} t' \mathbf{\dot q} (t) = \mathbf q_0 + \int_{t_0}^t \mathrm{d} t' \bigl( \mathbf v_0 + \mathbf g \: (t - t_0) \bigr) \\ &= \mathbf q_0 + \mathbf v_0\; \int_{t_0}^t \mathrm{d} t' + \mathbf g \; \int_{t_0}^t \mathrm{d} t' \;(t - t_0) \\ &= \mathbf q_0 + \mathbf v_0 \: (t - t_0) + \mathbf g \; \int_{0}^{t-t_0} \mathrm{d} t'' \: t'' \\ &= \mathbf q_0 + \mathbf v_0 \: (t - t_0) + \frac{1}{2} \: \mathbf g \: (t - t_0)^2 \end{align*} When we introduce the components of the vectors $\mathbf q$ and $\mathbf v = \dot{\mathbf q}$ as $\mathbf q = (q_1, q_2, \dots )$ and $\mathbf v = (v_1, v_2, \dots )$, and choose the component direction anti-parallel to $\mathbf g$ as $z = q_1$, then
\begin{align}
z(t) &= q_1(t) = z (t_0) + v_1 (t_0) \, (t-t_0) - \frac{g}{2} \: (t-t_0)^2 \tag{4.2.2a}\\\
q_i (t) &= q_i (t_0) + v_i (t_0) \, (t-t_0) \, , \quad \text{for } i > 1 \tag{4.2.2b}
\end{align}
It is illuminating to discuss these solutions form the perspective of non-dimensionalization and the evolution in phase space. For $i > 1$ the EOM is $\ddot q_i = 0$. In phase space the direction field at $(q_i, v_i)$ is then given by the vectors $( v_i(t_0), 0 )$ pointing in horizontal direction, as shown in Figure 4.2. Moreover, for Equation 4.2.2b we have $\dot q_i(t) = v_i(t_0) = \text{const}$ irrespective of $q_i(t)$. Therefore, the solutions take the form of horizontal lines. When introducing dimensionless units by adopting the velocity scale $v_i(t_0)$ one obtains \begin{align*} \hat v_i (t) = \frac{ \dot q_i (t) }{ \dot q_i(t_0) } = 1 \end{align*} For this problem all trajectories are identical up to a rescaling of the length and time units. By rescaling, all horizontal lines in the phase space can be mapped into the same dimensionless solution. From the point of view of the Buckingham-Pi (Theorem 1.1) this is due to the fact that there are no dimensionless parameters in the solutions—not even due to the choice of initial conditions.
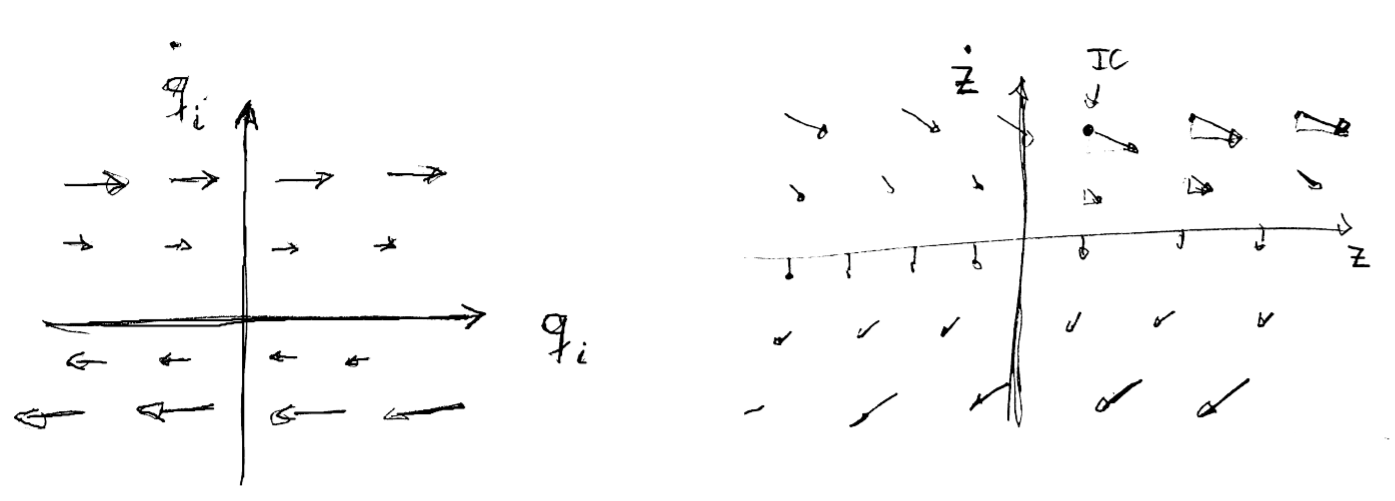Figure 4.2: Phase-space flows for motion for free flight.
(left) For direction perpendicular to $\mathbf g$
where there is no acceleration.
The trajectories are horizontal lines.
(right) For $z$ anti parallel to $\mathbf g$ there is a constant acceleration $-g$.
The trajectories take the form of parabola that are open to the left.}
For Equation 4.2.2a the arrows at position $(z,v_z)$ in the phase space are directed to $(v, -g)$. For $v=0$ they point straight down, for large $v$ they point right and only a little bit down, and for large negative $v$ they point left and only a little bit down, as marked in Figure 4.2 (right). The phase-space trajectories are found by observing that $\dot z = v_z (t_0) - g\, (t-t_0)$ implies $t-t_0 = \bigl[ v_z (t_0) - v_z \bigr]/g$ such that \begin{align} z &= z (t_0) + v_z (t_0) \, \frac{ v_z (t_0) - v_z }{g} - \frac{ \bigl[ v_z (t_0) - v_z \bigr]^2 }{ 2\, g } \nonumber \\ &= z (t_0) + \frac{ v_z (t_0) - v_z }{ 2\, g} \; \left[ 2 \, v_z (t_0) - \bigl( v_z (t_0) - v_z \bigr) \right] \nonumber \\ &= z (t_0) + \frac{ v_z^2 (t_0) - v_z^2 }{ 2\, g } \tag{4.2.3} \end{align}
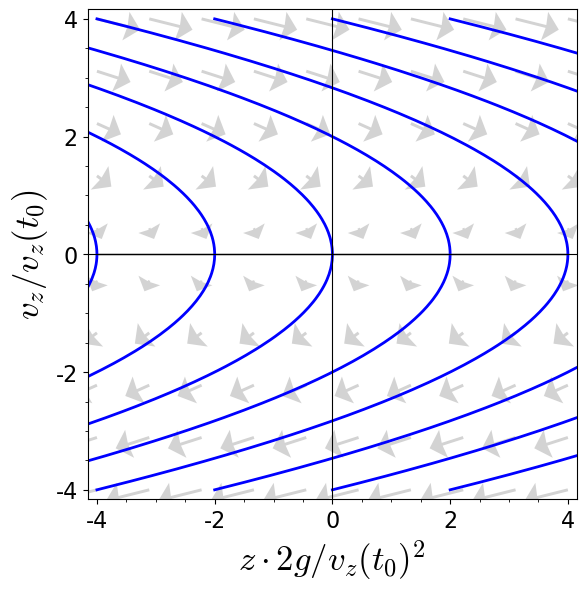Figure 4.3: Dimensionless phase-space trajectories of a particle falling in the gravitational field without friction.
As function of $v_z$ these are parabola with a maximum at $v_z=0$ and height $z_{\text{max}} = z (t_0) + v_z^2 (t_0) / 2g$, as shown in Figure 4.2 (right). In this case the EOM involves the constant $g$ such that only one of the initial conditions can be absorbed into dimensionless units. For dimensionless units based on the velocity scale $v_z (t_0)$ and the length scale $v_z^2 (t_0)/2\,g$ we have \begin{align*} \frac{ z }{ v_z^2 (t_0) / 2\,g } &= I - \left( \frac{ v_z }{ v_z(t_0) } \right)^2 \quad \text{with} \: I = 1 + \frac{ 2\, g \, z(t_0) }{ v_z^2 (t_0) } \end{align*}
The trajectories in this dimensionless representation are shown in Figure 4.3. They all have the shape of a normal parabola, but the parabolas are shifted by the dimensionless constant $I$ that is formed by the gravitational acceleration $g$, and the initial conditions $z(t_0)$ and $v_z(t_0)$.
4.2.4 Self Test
Problem 4.1: Estimating the depth of a pond
You drop a stone into a pond and count $n$ seconds till you hear it hit the water. How long a chord do you have to attach to your bucket to get up some water.
Problem 4.2: Integrating the EOM for the flight of an Earth-bound rocket
Integrate the EOM for rocket flight derived in Section 3.5, \begin{align*} \dot V_R(t) &= -g + \frac{ a \, \rho \, v_f^2 }{m+M_0 - a \, \rho \, v_f \, t} \\ \dot z(t) &= V_R(t) \end{align*} for a rocket that is launched with velocity $v_0$ at a height $H_0$, i.e., for the ICs \begin{align*} V_R(t_0) = v_0 \qquad\text{ and }\qquad z(t_0) = H_0 \end{align*} How do the solutions Equation 3.5.1a and Equation 3.5.1b change? Was there a way to anticipate the impact of the changing the initial height $H_0$?
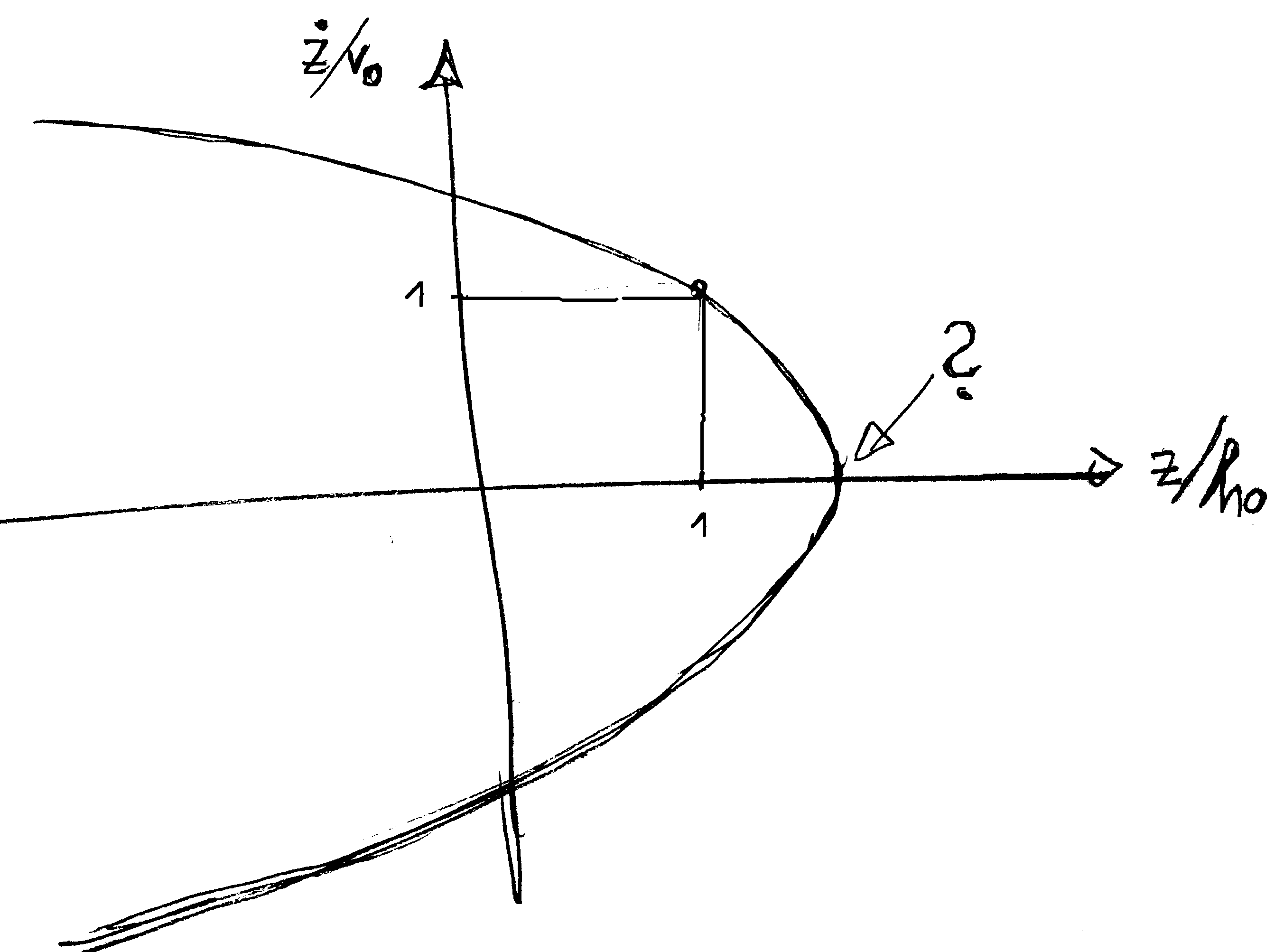Figure 4.4: Sketch of the universal form of the free-flight trajectories in phase space,
Equation 4.2.3.
Problem 4.3: Alternative dimensionless units for trajectories with constant acceleration
Discuss the shape of the trajectories that emerges
when introducing dimensionless units based on the velocity scale $v_z (t_0)$
and the length scale $z (t_0)$ into Equation 4.2.3.
Hint: