- 1.2 Dimensional analysis
1.2 Dimensional analysis
Mathematics does not know units. Experimental physicists hate large sets of parameters because the sampling of high-dimensional parameter space is tiresome. A remedy to both issues is offered by the Buckingham-Pi-Theorem. We state it here in a form accessible with our present level of mathematical refinement. The discussion of a more advanced formulation may appear as a homework problem later on on this course.
Theorem 1.1 Buckingham-Pi-Theorem
A dynamics with $n$ parameters,
where the positions $\mathbf q$ and the parameters involve the three units meter, seconds and kilogram,
can be rewritten in terms of a dimensionless dynamics
with $n-3$ parameters,
where the positions $\boldsymbol\xi$, velocities $\boldsymbol\zeta$,
and parameters $\pi_j$ with $j \in \{ 1, \dots, n-3\}$
are given solely by numbers.
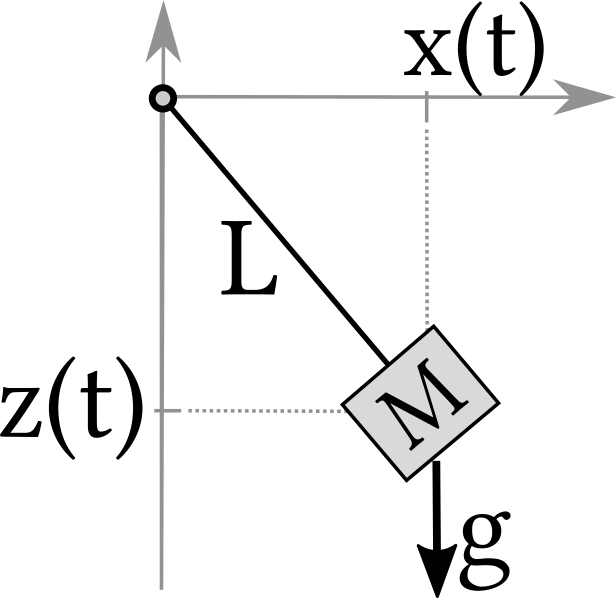Figure 1.2: Pendulum discussed in Example 1.8.
Example 1.8 Non-dimensionalization for a pendulum
Let $\mathbf x$ denote the position of a pendulum of mass $M$
that is attached to a chord of length $L$
and swinging in a gravitational field $\mathbf g$ of strength $g$
(see Figure 1.2).
The units of these quantities are
$[\mathbf x] = \text{m}$,
$[M] = \text{kg}$,
$[L] = \text{m}$, and
$[g] = \text{m/s$^2$}$, respectively.
The position $\mathbf x$ describes the position of the system.
Its evolution will depend (potentially) on the three parameters,
$M$, $L$, and $g$, plus the direction of $\mathbf g$.
In this problem we choose $L$ as length scale and $\sqrt{L/g}$ as time scale.
Then the dimensionless positions will be $\boldsymbol\xi = \mathbf x /L$,
the dimensionless velocities will be $\boldsymbol\zeta = \mathbf{\dot x} / \sqrt{g\, L}$.
There is no way to turn $M$ into a dimensionless parameter.
Therefore, the evolution of $(\xi, \zeta)$ can not depend on $M$.
The only dimensionless parameter that remains in the model is the direction of$\mathbf g$.
Example 1.9 Non-dimensionalization for the flight of a piece of chalk
Let $\mathbf x_1$ and $\mathbf x_2$ denote the position of the tip and the tail of a model for a piece of chalk,
where tip and tail are associated to masses $m_1$ and $m_2$.
The piece of chalk has a length $L$.
It performs a free flight in a gravitational field with acceleration $\mathbf g$ of strength $g$.
The units of these quantities are
$[\mathbf x_i] = \text{m}$,
$[m_i] = \text{kg}$,
$L = \text{m}$, and
$[g] = \text{m/s$^2$}$, respectively.
There are four parameters, $n=4$, plus the direction of $\mathbf g$.
In this problem we choose $L$ as length scale and $\sqrt{L/g}$ as time scale.
Then the dimensionless positions will be $\boldsymbol\xi_i = \mathbf x_i /L$,
the dimensionless velocities will be $\boldsymbol\zeta = \mathbf{\dot x}_i / \sqrt{g\, L}$.
The two masses $m_1$ and $m_2$ give rise to the dimensionless parameter $\pi_1 = m_1/m_2$,
and in three dimensions the direction of $\mathbf g$ must be characterized by another two dimensionless parameters.
Proof of the Buckingham-Pi-Theorem
We first look for combinations of the parameters with the following units
\begin{align*}
\text{m}
&= \left[ p_1^{\alpha_1} \right]\:\left[ p_2^{\alpha_2}\right] \: \dots \:\left[ p_n^{\alpha_n} \right]
\\
\text{s}
&= \left[ p_1^{\beta_1} \right]\:\left[ p_2^{\beta_2}\right] \: \dots \:\left[ p_n^{\beta_n} \right]
\\
\text{kg}
&= \left[ p_1^{\gamma_1} \right]\:\left[ p_2^{\gamma_2}\right] \: \dots \:\left[ p_n^{\gamma_n} \right]
\end{align*}
Each of these equations involves constraints on the exponents in order to match the exponents of the three units
that can be expressed as a system of linear equations.
The solvability conditions for such systems imply that they conditions can always be met by an appropriately chosen set of three parameters.
Without loss of generality we denote them as $p_1$, $p_2$ and $p_3$, and we have
\begin{align}
\text{m}
&= \left[ p_1^{\alpha_1} \right]\:\left[ p_2^{\alpha_2}\right] \: \left[ p_3^{\alpha_n} \right]
\nonumber\\
\text{s}
&= \left[ p_1^{\beta_1} \right]\:\left[ p_2^{\beta_2}\right] \: \left[ p_3^{\beta_n} \right]
\label{eq:epressSI}\\ \nonumber
\text{kg}
&= \left[ p_1^{\gamma_1} \right]\:\left[ p_2^{\gamma_2}\right] \: \left[ p_3^{\gamma_n} \right]
\end{align}
Thus we use the parameters $p_1, \dots, p_3$ to remove the units from our description.
In its dimensionless form it will involve the positions and velocities
\begin{align*}
\boldsymbol\xi
&= \mathbf q \: p_1^{-\alpha_1} \: p_2^{-\alpha_2} \: p_3^{-\alpha_n}
\\
\boldsymbol\zeta
&= \dot{\mathbf q} \: p_1^{\beta_1-\alpha_1} \: p_2^{\beta_2-\alpha_2} \: p_3^{\beta_n-\alpha_n}
\end{align*}
Similarly, the dimensionless form of the parameters $p_i$ of the dynamics are obtained by
multiplying the original parameters with appropriate powers of the expressions \eqref{eq:epressSI} of the units.
For $p_1$ to $p_3$ this gives rise to one.
Additional parameters will turn into dimensionless groups of parameters that provide $\pi_1$ to $\pi_{n-3}$.
$\rule{4mm}{4mm}$
Self Test
Problem 1.3:
Oscillation period of a particle attached to a spring
In a gravitational field with acceleration $g_{\text{Moon}}=1.6\,\text{m/s$^2$}$
a particle of mass $M=100\,\text{g}$
is hanging at a spring with spring constant $k=1.6\,\text{kg/s$^2$}$.
It oscillates with period $T$ when it is slightly pulled downwards and released.
We describe the oscillation by the distance $x(t)$ from its rest position.
- Determine the dimensionless distance $\xi(t)$,
and the associated dimensionless velocity$\zeta(t)$. - Provide an order-of-estimate guess of the oscillation period $T$.
Problem 1.4:
Earth orbit around the sun
- Light travels with a speed of $c \approx 3 \times 10^{8}\,\text{m/s}$, and it takes $500\,\text{s}$ to travel from Sun to Earth. What is the Earth-Sun distance$D$, i.e., one Astronomical Unit (AU) in meters?
- The period of the trajectory of the Earth around the Sun depends on $D$, on the mass $M = 2 \times 10^{30}\,\text{kg}$ of the sun, and on the gravitational constant $G = 6.7 \times 10^{-11}\,\text{m$^3$/kg s$^2$}$. Estimate, based on this information, how long it takes for the Earth to travel once around the sun.
- Express your estimate in terms of years. The estimate of (b) is of order one, but still off by a considerable factor. Do you recognize the numerical value of this factor?
- Upon discussing the trajectory $\mathbf x(t)$ of planets around the sun later on in this course, we will introduce dimensionless positions of the planets $\boldsymbol\xi(t) = \mathbf x(t) / L = ( x_1(t)/L, x_2(t)/L, x_3(t)/L)$. How would you define the associated dimensionless velocities?