Table of Contents
6.3 Dynamics with one degree of freedom
We will now illustrate the application of the Lagrange formalism for three examples
with a single degree of freedom of the motion:
- The mathematical pendulum, Example 6.1, will give a first idea of how to find EOMs with the Lagrange formalism. This EOM can also easily be found by other approaches. It serves here to illustrate problems where one adopt 2D polar coordinates.
- The motion of a pearl on a rotating ring constitutes a system with an explicit time dependence. In that case the Lagrange formalism dramatically simplifies the the derivation of the EOM. We will also discuss for this model how to account for dissipative forces and we will see how the solutions of a problem can change qualitatively upon varying a parameter. In this example we will adopt spherical coordinates.
- The motion of a weight on a carousel we will discussed as an example of a system that needs a dedicated treatment for the description of admissible positions. The discussion will be based on cylindrical coordinates.
6.3.1 The EOM for the mathematical pendulum
The parameterization introduced in Example 6.1 provides the kinetic energy \begin{align*} T = \frac{M}{2} \, \dot{\mathbf x}^2 = \frac{M}{2} \, L^2 \, \dot\theta^2 \: \hat{\boldsymbol\theta}(\theta(t))^2 = \frac{M}{2} \, L^2 \, \dot\theta^2 \end{align*} and the potential energy in the gravitational field \begin{align*} U = - M \mathbf g \cdot \mathbf x = - M\, L \: \hat{\mathbf R}\bigl(\theta(t)\bigr) \cdot \mathbf g = -M\, L\, g \cos\theta(t) \end{align*} since $\mathbf g = g \:\hat{\mathbf R}\bigl(0\bigr) $. Consequently, \begin{align} \nonumber \mathcal L &= \frac{M}{2} \, L^2 \, \dot\theta^2 + M\, g\, L\, \cos\theta(t) \\ \nonumber \Rightarrow\quad M \, L^2 \: \ddot \theta(t) &= \frac{\mathrm{d}}{\mathrm{d} t} \frac{\partial \mathcal L}{\partial \dot \theta} = \frac{\partial \mathcal L}{\partial \theta} = - M\, g\, L\, \sin\theta(t) \\ \Rightarrow\qquad \ddot \theta(t) &= -\frac{g}{ L} \; \sin\theta(t) \tag{6.3.1} \end{align} The EOM 6.3.1 can be integrated once by multiplication with $2\dot\theta(t)$ \begin{align} \dot\theta^2(t) - \dot\theta^2(t_0) &= \int_{t_0}^t \mathrm{d} t \: 2 \dot\theta \ddot\theta = \int_{t_0}^t \mathrm{d} t \: 2 \dot\theta \left( -\frac{g}{ L} \; \sin\theta(t) \right) \nonumber\\ \nonumber &= 2 \; \int_{\theta(t_0)}^{\theta(t)} \mathrm{d} \theta \: \frac{\mathrm{d}}{\mathrm{d} \theta} \left( \frac{g}{ L} \; \cos\theta \right) = 2 \; \frac{g}{ L} \; \bigl( \cos\theta(t) - \cos\theta(t_0) \bigr) \end{align} This is a Mattheiu differential equation. For most initial conditions it can not be solved by simple means. However, the first integral provides the phase-space trajectories $\dot\theta(\theta)$ for every given set of initial conditions $\bigl( \theta(t_0), \dot\theta(t_0) \bigr)$,
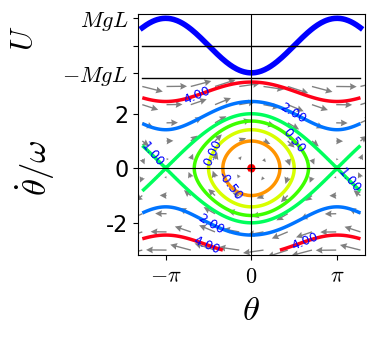
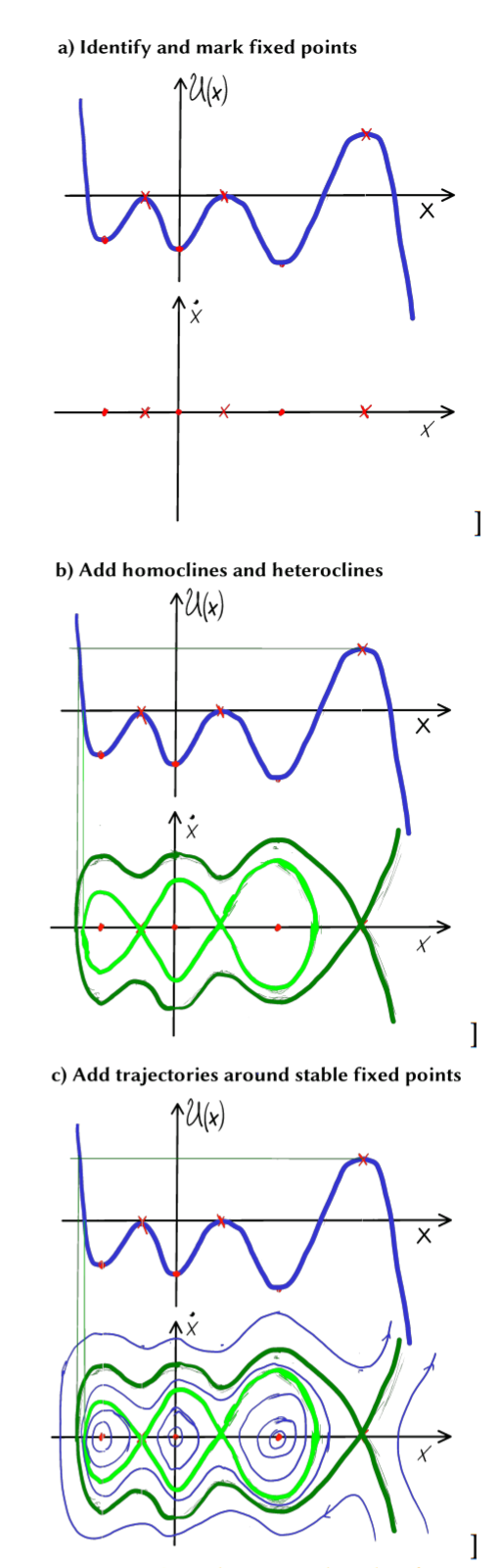
Figure 6.5: The potential $U(\theta)$ (top) and the phase-space plot (bottom) for the EOM EOM 6.3.1 of the mathematical pendulum. The numbers marked on the contour lines indicated the energy of a trajectory in units of $MgL$.
\begin{align*}
\dot\theta
= \pm\sqrt{ \dot\theta^2(t_0) + \frac{2\,g}{ L} \; \bigl( \cos\theta(t) - \cos\theta(t_0) \bigr) }
\end{align*}
The phase-space portrait is shown in Figure 6.5.
There are trivial solutions where the pendulum is resting without motion at its stable and unstable rest positions $\theta = 0$ and $\theta = \pi$,
These positions are denoted as fixed points of the dynamics.
There are closed circular trajectories close to the minimum, $\theta=0$, of the potential
where it is harmonic to a good approximation.
These are solutions with energies $0 < 1 + E/MgL \lesssim 1$.
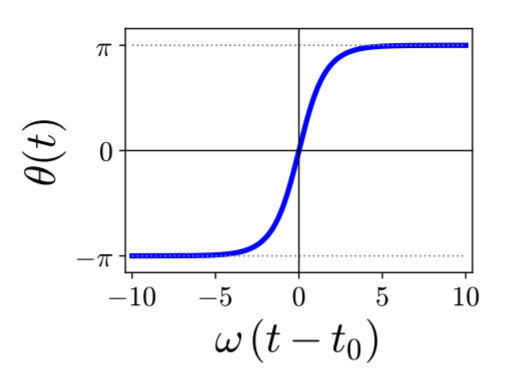
For larger amplitudes the amplitude of the swinging grows, and the circular trajectories get deformed. When $E$ approaches $MgL$ the phase-space trajectories arrive close to the tipping points $\theta = \pm\pi$ where they form very sharp edges. For $\theta$ close to $\theta = \pm\pi$ the trajectories look like the hyperbolic scattering trajectories for the potential $-a\,x^2/2$ that was discussed in Problem 4.25. When the non-dimensional energy is exactly one, the pendulum starts on top, goes through the minimum and returns to the top again. Apart from the fixed points, this is the only case where the evolution can be obtained in terms of elementary functions. For the initial condition $\dot\theta(t_i)=0$ and $\cos\theta_i = -1$ we find \begin{align*} \omega^{-1} \; \dot \theta_H(t) &= \pm \sqrt{ 2 + 2 \, \cos\theta_H(t) } = \pm 2 \; \cos\frac{\theta_H(t)}{2} \end{align*} The same equation is also obtained for the initial condition $\theta_0 = 0$ and $\dot\theta(t_0)=\sqrt{2g/ L}$ half-way on the way from the top back to the top. For this initial condition the ODE for $\dot\theta_H$ can be integrated, and we find \begin{align} \nonumber \pm 2\,\omega \, (t - t_0) &= \int_{0}^{\theta(t)} \frac{\mathrm{d} \theta}{\cos\frac{\theta}{2}} = \ln \tan \frac{ \theta + \pi }{4} \\ \Rightarrow\qquad \theta_H(t) &= -\pi + 4 \: \arctan \mathrm{e}^{\pm 2\omega \; (t-t_0)} \tag{6.3.2} \end{align} The $\pm$ signs account for the possibility that the pendulum can move clockwise and counterclockwise. The counterclockwise trajectory is shown in Figure 6.6. In the limit $t \to -\infty$ it starts in the unstable fixed point $\theta=-\pi$. It falls down till it reaches the minimum $\theta=0$ at time $t_0$, and then it rises again, reaching the maximum $\theta = \pi$ for time $t \to \infty$. Such a trajectory is called a homocline.
Definition 6.6 Homoclines and Heteroclines
Homoclines and heteroclines are trajectories that approach a fixed points of a dynamics in their infinite past and future.
A homocline returns to the same fixed point from where it started.
A heterocline connects two different fixed points.
The take-home message of this example is that the minima and maxima of a potential organize the phase space flow. Close to each minimum a conservative system will have closed trajectories that represent oscillations in a potential well. The well is confined by maxima to the left and right of the minimum of the potential. When these maxima have different height there is a homoclinic orbit coming down from and returning to the shallower maximum. When they have the same height, they are connected by heteroclinic orbits. Thus, the homoclines and heteroclines divide the phase space into different domains. Initial conditions within the same domain show qualitatively the same dynamics. Initial conditions in different domains feature qualitatively different dynamics. For the mathematical pendulum the heteroclines divide phase space into three domains, up to the $2\pi$ translation symmetry of $\theta$:
- There are trajectories oscillating around $\theta = 0$, with energies smaller than $MgL$. The region of these oscillations is bounded by the heteroclines provided in Equation 6.3.2.
- Trajectories with initial conditions lying above the anticlockwise moving heterocline will persistently rotate anticlockwise and never reverse their motion.
- Trajectories with initial conditions lying below the clockwise moving heterocline will persistently rotate clockwise and never reverse their motion.
The general strategy for sketching phase-space plots is summarized in the following algorithm and illustrated in Figure 6.7.
Algorithm 6.2 Phase space plots
- Identify the minima and maxima of the potential. Mark the minima as (marginally) stable fixed points with velocity zero. Mark the maxima as unstable fixed points with velocity zero.
- Identify the fate of trajectories departing from the unstable fixed points. Identify to this end the closest positions on the potential that have the same height as the maximum. When it is another extremum the orbit will form an heterocline. Otherwise, it will be reflected and return to the initial maximum, forming a homocline. If there is no further point of the same height, the trajectory will escape to infinity.
- Add characteristic trajectories close to the minima, in between and outside of homo- and heteroclines.
In these steps it is advisable to
- Observe the symmetries of the system. To the very least the plot is symmetric with respect to reflection at the horizontal axis, i.e., swapping the sign of the velocity.
- Observe energy conservation (if it applies): The modulus of the velocity takes a local minimum for a maximum of the potential, and a local maximum for a minimum of the potential.
6.3.2 The EOM for a pearl on a rotating ring
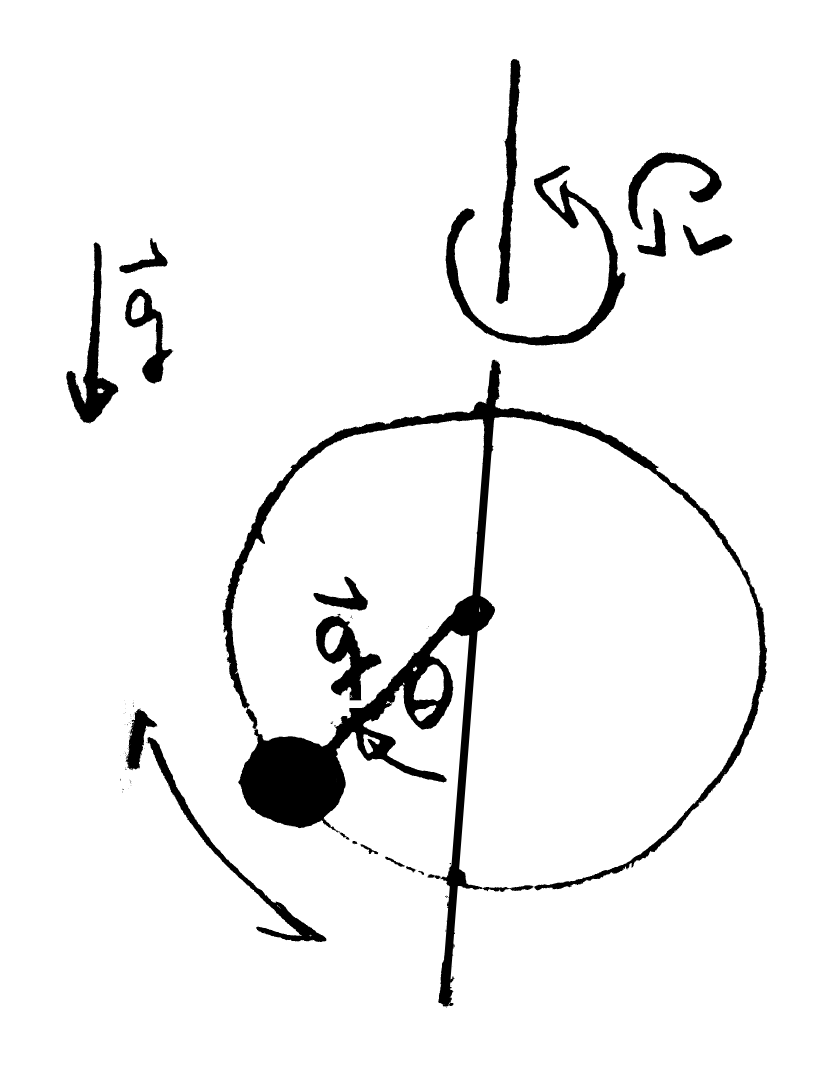
We consider a pearl of mass $M$ that can freely move on a ring. The ring is mounted vertically in the gravitational field and it spins with angular velocity $\Omega$ around its vertical symmetry axis. The setup constrains the position of the pearl to lie on a spherical shell. The position of the pearl on the ring is fully described by the angle $\theta(t)$ of the deflection of the pearl from the direction of gravity (see Figure 6.8. In addition we must specify the orientation of the ring. This will be done by the angle $\phi(t) = \Omega t$ that enters as a parameter in this time-dependent problem. Hence, the position of the pearl is most conveniently specified in terms of polar coordinates $(R, \theta, \phi)$ where $R$ takes the constant value $ L$, and $\phi(t) = \Omega t$ enters as a time-dependent parameter.
Theorem 6.3 Basis vectors for spherical coordinates
Let $\{ \hat{\boldsymbol x}, \hat{\boldsymbol y}, \hat{\boldsymbol z} \}$ be a fixed cartesian basis of $\mathbb R^3$, and
$(R,\theta,\phi)$ be the spherical coordinates associated to a point $(x,y,z) \in \mathbb R^3$.
Then
- $R = \sqrt{x^2+y^2+z^2}$ is the distance from the origin
- $\theta = \arctan(\sqrt{x^2+y^2}/z)$ is the angle with respect to $\hat{\boldsymbol z}$,
- $\phi = \arctan(y/x)$ the angle with respect to $\hat{\boldsymbol x}$ of the projection of the position into the $(x,y)$ plane.
We denote the vector from the origin to $(R,\theta,\phi)$ as $R \: \hat{\boldsymbol R}(\theta, \phi)$. Then the following statements apply
- $\hat{\boldsymbol \theta} = \partial_\theta \hat{\boldsymbol R}$ is a vector pointing along the grant circle of the unit sphere selected by $(\theta,\phi)$ and $\hat{\boldsymbol z}$
- $\hat{\boldsymbol \phi} = \hat{\boldsymbol R} \times \hat{\boldsymbol \theta}$ is a vector tangential to the unit sphere at $(\theta,\phi)$ and vertical to $\hat{\boldsymbol z}$
- For every $\theta \in [0,\pi]$ and $\phi\in [0, 2\pi)$ the vectors $\{ \hat{\boldsymbol R}, \hat{\boldsymbol \theta}, \hat{\boldsymbol \phi}\}$ form a right-handed orthonormal basis of $\mathbb R^3$.
Remark 6.5. The directions of the basis vectors $\{ \hat{\boldsymbol R}, \hat{\boldsymbol \theta}, \hat{\boldsymbol \phi}\}$ depend on $\theta$ and $\phi$.
Theorem 6.4 Derivatives of the basis vectors for spherical coordinates
The partial $\theta$ and $\phi$ derivatives of the basis vectors $\{ \hat{\boldsymbol R}, \hat{\boldsymbol \theta}, \hat{\boldsymbol \phi}\}$ obey the following relations
\begin{align} \nonumber
\partial_\theta \hat{\boldsymbol R} &= \hat{\boldsymbol \theta} & \partial_\phi \hat{\boldsymbol R} &= \sin\theta \: \hat{\boldsymbol \phi}
\\
\partial_\theta \hat{\boldsymbol \theta} &= -\hat{\boldsymbol R} & \partial_\phi \hat{\boldsymbol \theta} &= \cos\theta \: \hat{\boldsymbol \phi} \tag{6.3.3}
\\ \nonumber
\partial_\theta \hat{\boldsymbol \phi} &= 0 & \partial_\phi \hat{\boldsymbol \phi} &= -\sin\theta \: \hat{\boldsymbol R} - \cos\theta \: \hat{\boldsymbol \theta}
\end{align}
Proof. The proofs of Theorem 6.3 and Theorem 6.4 are given as Problem 6.6. qed
In polar coordinates the position of the pearl is \begin{align*} \mathbf x (t) = L \, \hat{\mathbf R}\bigl(\theta(t), \phi(t) \bigr) \end{align*} We adopt the Lagrange formalism to determine the equation of motion for $\theta(t)$, which is the only coordinate in this setting. (The motion of the pearl has a single degree of freedom.) The potential energy takes the same form as for the pendulum, \begin{align*} U = - M \: \mathbf g \cdot \mathbf x = -M\, g\, L\, \cos\theta(t) \, . \end{align*} The kinetic energy is obtained based on its velocity \begin{align*} \dot{\mathbf x} &= L \; \frac{\mathrm{d}}{\mathrm{d} t} \hat{\boldsymbol R}(\theta(t), \Omega t) = L \: \dot\theta \: \partial_\theta \hat{\boldsymbol R}(\theta(t), \Omega t) + L \, \Omega \: \partial_\phi \hat{\boldsymbol R}(\theta(t), \Omega t) \\ &= L \, \dot\theta \: \hat{\boldsymbol\theta}\bigl( \theta(t), \Omega t \bigr) + L \, \Omega \: \sin\theta(t) \; \hat{\boldsymbol\phi}\bigl( \theta(t), \Omega t \bigr) \end{align*} which provides the Lagrange function \begin{align*} \mathcal L (\theta , \dot\theta ) = \frac{M}{2} \, L^2 \, \dot\theta^2 + \frac{M}{2} \, L^2 \: \Omega^2 \: \sin^2\theta(t) + M\, g\, L\, \cos\theta(t) \end{align*} It only differs from the expression for the spherical pendulum by the fact that $\phi(t)$ is not a coordinate whose evolution must be determined from an EOM. Rather it is a parameter $\phi(t) = \Omega\,t$ provided by the setting of the problem. The motion only has a single DOF, $\theta(t)$, with EOM \begin{align} \ddot \theta(t) &= - \frac{g}{ L}\; \sin\theta(t) \; \left( 1 - \frac{ L\, \Omega^2}{g} \; \cos\theta(t) \right) \tag{6.3.4} \end{align} This EOM can once be integrated by the same strategy adopted for the swing and the spherical pendulum. Thus, one finds the effective potential \begin{align*} U_{\text{eff}}(\theta) = -\omega^2\; \cos\theta \; \left[ 1 - \left( \frac{\Omega}{\omega} \right)^2 \; \cos\theta \right] \tag{6.3.5} \end{align*}
Figure 6.9 shows the effective potential and phase space portraits for different values of angular momentum, i.e., of the dimensionless control parameter $\kappa = \Omega/\omega$. For $\kappa < 1$ the phase space has the same structure as that of a mathematical pendulum, with a stable fixed point at $\theta = 0$. When $\kappa$ passes through one, this minimum of $U_{\text{eff}}$ turns into a maximum, and two new minima emerge at the positions \begin{align} \theta_c = \pm \arccos\kappa^{-2} = \pm \arccos \left( \frac{\omega}{\Omega} \right)^2 \tag{6.3.6} \end{align} that are indicated by a dotted gray line in the left panel of Figure 6.9. The new maximum at zero is always shallower than the maxima at $\pm\pi$. Hence, it gives rise to two homoclinic orbit that wind around the new stable fixed points. The maxima at $\pm\pi$ will further we connected by heteroclinic orbits. Hence, phase space is divided into five distinct regions. For energies smaller than $U_{\text{eff}} (\theta=0)$ the trajectories wiggle around one of the stable fixed points. They stay on one side of the ring and oscillate around the angle $\theta_c$. There are two regions of this type because the pearl can stay on both sides of the ring. For $U_{\text{eff}}(\theta=0) < E < U_{\text{eff}}(\theta=\pi)$ the trajectories show oscillations back and forth between the two sides of the ring, For $E > U_{\text{eff}}(\theta=\pi)$ they rotate around the ring in clockwise or counter-clockwise direction for $\dot\theta < 0$ or $\dot\theta > 0$, respectively.
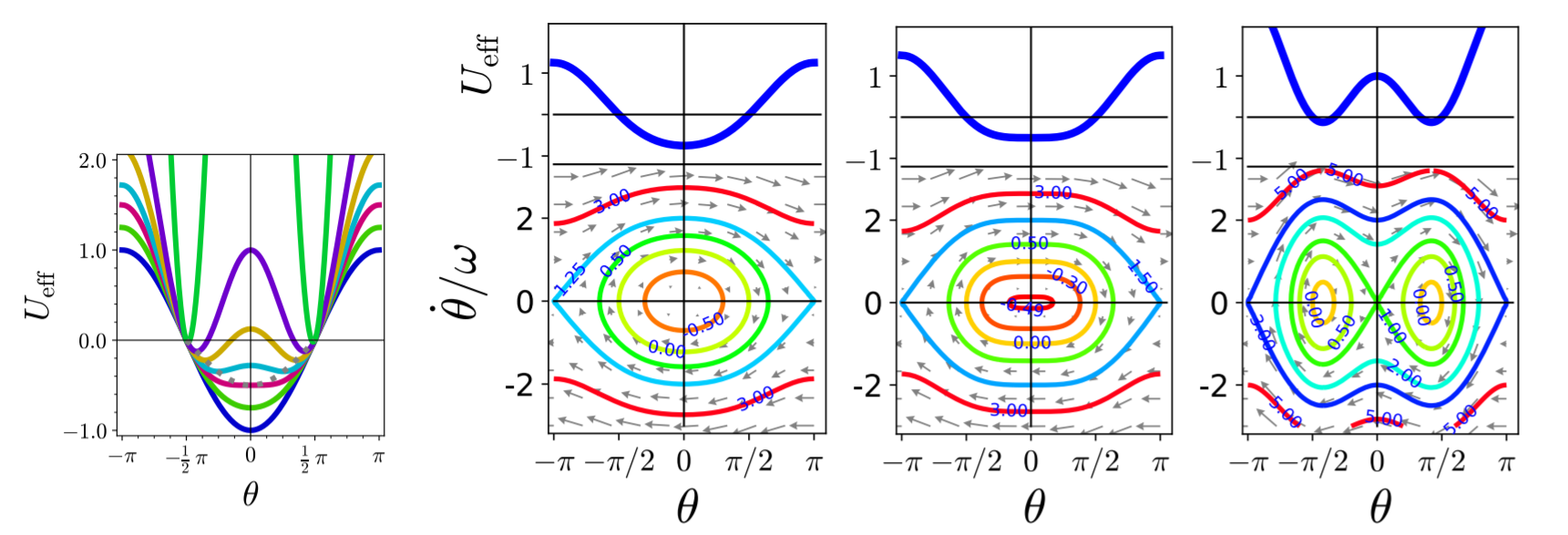 Figure 6.9: The left panel shows the effective potential for the pearl on a ring for parameter values $(\Omega/\omega) \in \{ 0, 2^{-1/2}, 1, 1.2, 1.5, 2, 5 \}$ from bottom to top. The subsequent panels show phase-space portraits of the motion for $\Omega/\omega = 2^{-1/2}$, $1$, and$2$, respectively.
Figure 6.9: The left panel shows the effective potential for the pearl on a ring for parameter values $(\Omega/\omega) \in \{ 0, 2^{-1/2}, 1, 1.2, 1.5, 2, 5 \}$ from bottom to top. The subsequent panels show phase-space portraits of the motion for $\Omega/\omega = 2^{-1/2}$, $1$, and$2$, respectively.
There are two take-home message from this example:
1) There are no conservation laws in the dynamics when there are explicitly time-dependent constraints.
Hence, the strategies of Chapter 4 to establish and discuss the EOM can no longer be applied.
However, the Lagrange formalism still provides the EOM in a straightforward manner.
2) In general, the structure of the phase-space flow changes upon varying the dimensionless control parameters of the dynamics. These changes are called bifurcations, and they are a very active field of contemporary research in theoretical mechanics. The pearl on the ring features a pitchfork bifurcation since the positions of the fixed points resemble the shape of a pitch fork (see Figure 6.10).
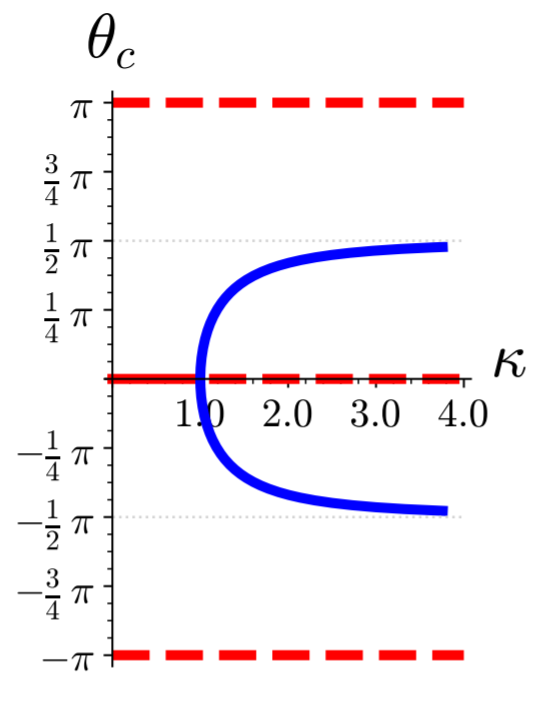
Figure 6.10: Parameter dependence of the positions of the fixed points of the rotation governor.
Solid lines mark stable fixed points,
and unstable fixed points are marked by dashed lines.
Definition 6.7 Pitchfork bifurcation
Upon variation of a parameter $p$ a stable fixed point $x_*$ of a one-dimensional ODE
may loose stability at some parameter $p_c$, turning into an unstable fixed point.
In that case one will encounter one of the following scenarios:
- supercritical pitchfork bifurcation At $p_c$ two new stable fixed points emerge to its left and right of $x_*$.
- subcritical pitchfork bifurcation There were unstable fixed points to the left and right of $x_*$ that merge with $x_*$ at the parameter $p_c$.
Subseqeuntly there is only a single unstable fixed point.
Remark 6.6. The supercritical pitchfork bifurcation is commonly simply denoted as pitchform bifurcation.
Remark 6.7. In classical mechanics a pitchfork bifurcation, Figure 6.10, emerges whenever a minimum of a potential is dented to turn it into a maximum that is then surrounded minima on both sides, as shown in Figure 6.9. The supercritical pitchfork bifurcation refers to a situation where we initially have a minimum surrounded by two maxima, and then the minimum is pushed until it disappears. When this happens the maxima approach each other, and eliminate the dent in between. An example is provided in Problem 6.8.
6.3.3 Centrifugal Governor
The sharp increase of $\theta_c$ in Equation 6.3.6, when the rotation frequency $\omega$ rises beyond $\Omega$ is used in a feedback mechanism of the governor to control the rotation speed of steam engines (Figure 6.11).
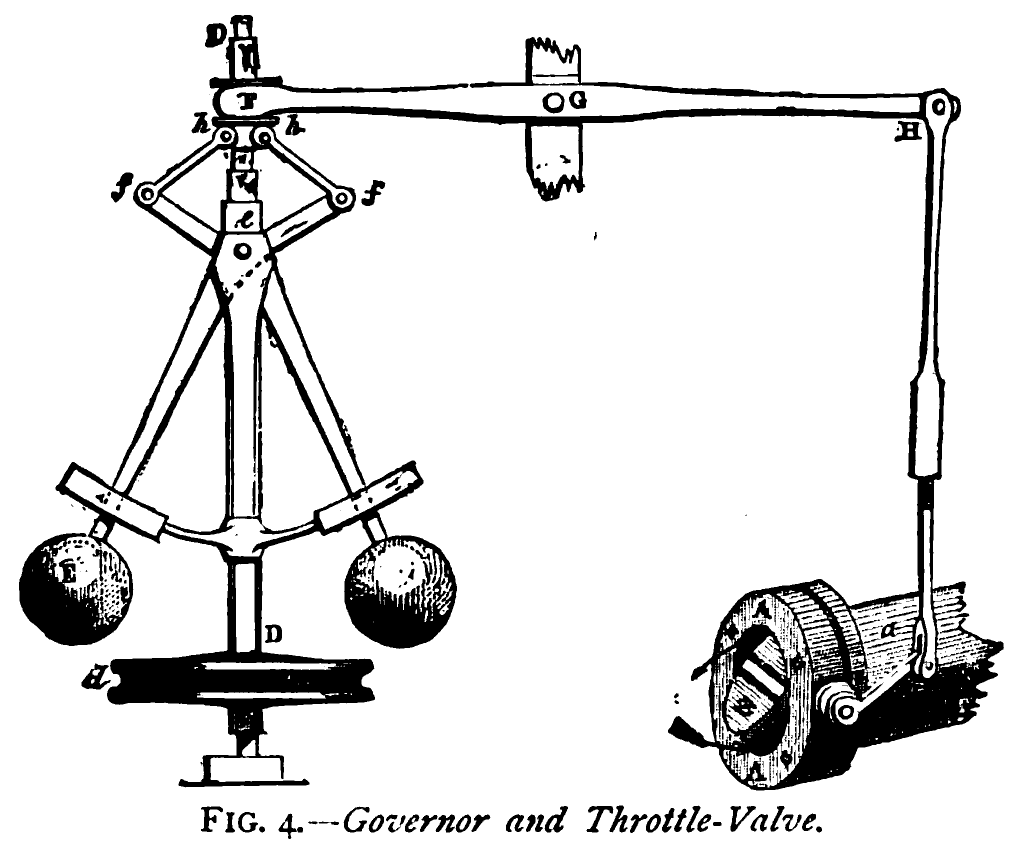 Figure 6.11: Rotational governor and throttle valve. When the rotation speed exceeds a critical value
the weights move outward and the arm opens a valve that reduces pressure in the steam engine.
Figure 6.11: Rotational governor and throttle valve. When the rotation speed exceeds a critical value
the weights move outward and the arm opens a valve that reduces pressure in the steam engine.
(Image from “Discoveries & Inventions of the Nineteenth Century” by R. Routledge, 13th edition, published 1900, Public domain, via Wikimedia Commons)
Oscillations around the stable fixed points is an undesirable feature of the governor such that some dissipation is welcome. We revisit Equation 6.2.1 to extend the Lagrange formalism for forces that do not derive from a potential \begin{align*} 0 &= - \int_{t_I}^{t_F} \mathrm{d} t \:\frac{\mathrm{d}}{\mathrm{d} t} \left( \delta\mathbf x \cdot m \, \dot{\boldsymbol x} \right) = - \int_{t_I}^{t_F} \mathrm{d} t \: \left( \delta\dot{\boldsymbol x} \cdot m \, \dot{\boldsymbol x} + \delta\mathbf x \cdot m \, \ddot{\boldsymbol x} \right) \\ &= - \int_{t_I}^{t_F} \mathrm{d} t \: \left( \delta\dot{\boldsymbol x} \cdot \nabla_{\dot{\boldsymbol x}} \mathcal L + \delta\mathbf x \cdot m \, \bigl( \mathbf F_d - \nabla_{\mathbf x}\Phi \bigr) \right) \\ &= \int_{t_I}^{t_F} \mathrm{d} t \: \delta\mathbf x \; \left( -\mathbf F_d + \nabla_{\mathbf x}\mathcal L - \frac{\mathrm{d}}{\mathrm{d} t} \nabla_{\dot{\boldsymbol x}} \mathcal L \right) \end{align*} Thus, and additional dissipative force $\mathbf F_d = -\gamma \, \dot\theta \: \hat{\boldsymbol \theta}$ will give rise to an additional additive term in Equation 6.3.4 such that the rotational governor has an EOM \begin{align*} \ddot \theta(t) &= - \frac{g}{ L}\; \sin\theta(t) \; \left( 1 - \frac{ L\, \Omega^2}{g} \; \cos\theta(t) \right) - \frac{\gamma}{M} \: \dot\theta(t) \end{align*} and the energy evolves as \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{\dot\theta^2}{2} + U_{\text{eff}}(\theta) \right) = - \frac{\gamma}{M} \: \dot\theta^2(t) \end{align*} Small friction deflects the trajectories towards smaller values of the effective potential, until the system comes to rest in a stable fixed point. For $\Omega/\omega = 2$ the impact of dissipation $\gamma/M = 0.2$ and $2.0$ is shown in Figure 6.12.
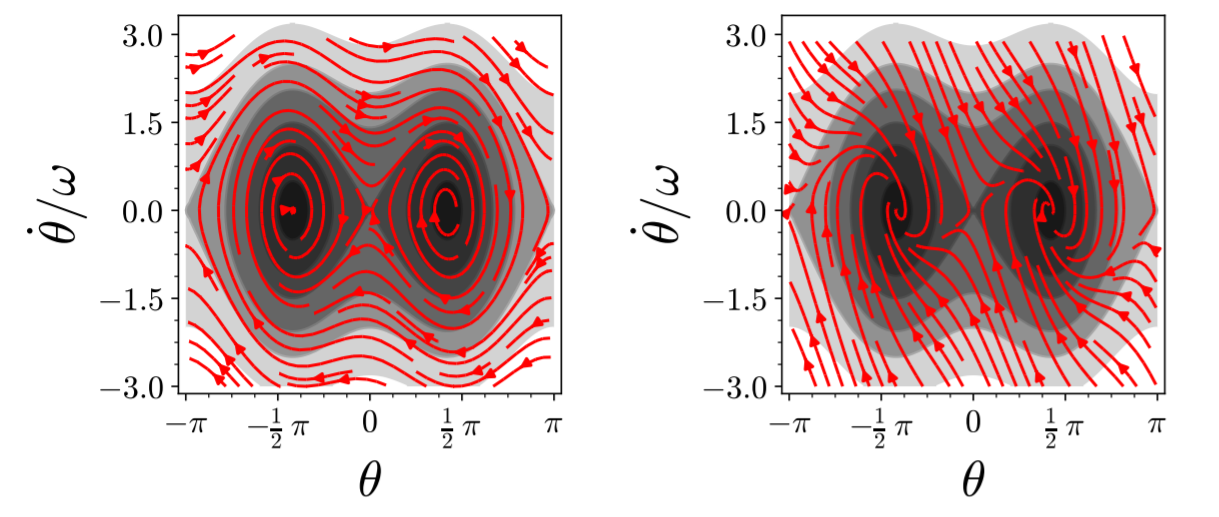 Figure 6.12: Phase-space plot for a rotational governor with rotation frequency $\Omega = 2\omega$.
The colors of gray in the background show contour levels of the energy.
The streamlines indicated the evolution of the dynamics for
(left) weak dissipation, $\gamma=0.2$, and
(right) strong dissipation, $\gamma=2$, dissipation.
Due to dissipation the trajectories acquire a component downwards in energy.
Figure 6.12: Phase-space plot for a rotational governor with rotation frequency $\Omega = 2\omega$.
The colors of gray in the background show contour levels of the energy.
The streamlines indicated the evolution of the dynamics for
(left) weak dissipation, $\gamma=0.2$, and
(right) strong dissipation, $\gamma=2$, dissipation.
Due to dissipation the trajectories acquire a component downwards in energy.
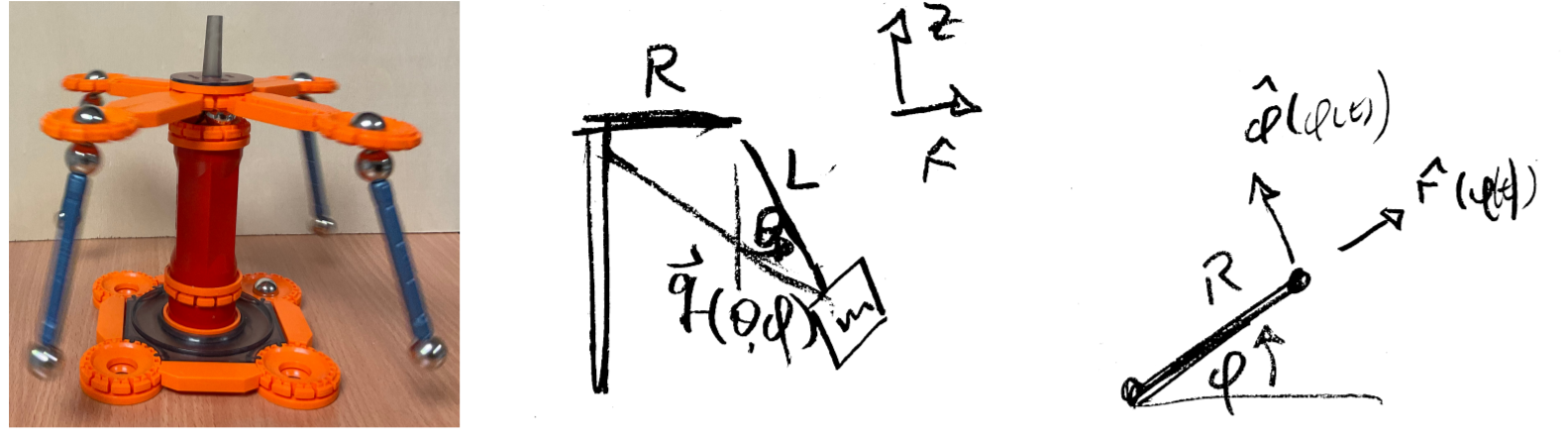
6.3.4 Carousel
The positions in the systems that we treated so far were described in terms of polar coordinates (mathematical pendulum, Section 6.3.1) and spherical coordinates (pearl on a rotating ring, Section 6.3.2). We will now address a system where we adopt cylindrical coordinates to describe particle positions: the motion of the beats of a toy carousel that is shown in Figure 6.13. The carousel is composed of four cantilever beams of length $R$ that extend outwards from a vertical axis that is rotating with angular velocity$\Omega$. At the far end of each beam there is a pendulum attached that freely swings in outward direction. The inclination of the pendulum arm towards gravity will be denoted as $\theta$. (Oscillations parallel to the motion of the beams are not be considered.) The pendulum arm has a length $L$ and it carries a weight $m$. Due to a magnetic contact the pendulum experiences minimal friction in its motion. Henceforth we the focus on the motion of one of the beats.
We pick the origin of the coordinate system on the ration axes right on the height of the cantilever. The rotation is around the vertical axes characterized the the unit vector $\hat{\boldsymbol z}$. Looking from the top (right panel of Figure 6.13) the pendulum arm sticks out in direction $\phi = \Omega t$. We adopt polar coordinates, as introduced in Remark 6.3, in the horizontal plane vertical to $\hat{\boldsymbol z}$. We denote the position of the fulcrum of the pendulum as $\mathbf R = R \: \hat{\boldsymbol r}(\phi)$, and express the vector from the fulcrum to the weight as $L\, \sin\theta \: \hat{\boldsymbol r}(\phi) - L \, \cos\theta \hat{\boldsymbol z}$. This amounts to a representation of the position of the mass in terms of cylindrical coordinates.
Theorem 6.5: Basis vectors for cylindrical coordinates
Let $\{ \hat{\boldsymbol x}, \hat{\boldsymbol y}, \hat{\boldsymbol z} \}$ be a basis of $\mathbb R^3$, and
$(R = \sqrt{x^2+y^2}, \phi=\tan(y/x), z)$
be the cylindrical coordinates associated to a point with cartesian coordinates $(x,y,z)$.
Then
- $R = \sqrt{x^2+y^2}$ is the distance of the point from the $\hat{\boldsymbol z}$ axis
- $\phi = \arctan(y/x)$ the angle with respect to $\hat{\boldsymbol x}$ of the projection of the position into the $(x,y)$ plane.
We denote the vector from the origin to $(R,\phi,z)$ as $\mathbf x = z \: \hat{\boldsymbol z} + R \: \hat{\boldsymbol R}(\phi)$. Then, the following statements apply
- $\hat{\boldsymbol \phi} = \partial_\phi \hat{\boldsymbol R}$ and $\hat{\boldsymbol z}$ are the horizontal and vertical unit vectors tangential to the surface of a cylinder with axis pointing along $\hat{\boldsymbol z}$
- For every $\phi \in [0,2\pi)$ the vectors $\{ \hat{\boldsymbol R}(\phi), \hat{\boldsymbol \phi}(\phi), \hat{\boldsymbol z}\}$ form a right-handed orthonormal basis of $\mathbb R^3$.
The $\phi$-derivatives of $\hat{\boldsymbol R}$ and $\hat{\boldsymbol \phi}$ follow the same rules as for polar coordinates, Theorem 6.1.
Proof. The proof is left to the reader. qed
The position $\mathbf x$ and the velocity $\dot{\boldsymbol x}$ of the weight attached to the carousell are \begin{align*} \mathbf x &= ( R + L\, \sin\theta) \: \hat{\boldsymbol r}(\Omega t) - L \, \cos\theta \hat{\boldsymbol z} \\ \dot{\boldsymbol x} &= ( R + L\, \sin\theta) \: \Omega \: \hat{\boldsymbol \phi}(\Omega t) + L\, \cos\theta \: \dot\theta \: \hat{\boldsymbol r}(\Omega t) + L \, \sin\theta \: \dot\theta \hat{\boldsymbol z} \end{align*} The kinetic energy and potential energy are \begin{align*} T &= \frac{m}{2} \: \dot{\mathbf x}^2 = \frac{m}{2} \left[ L^2 \: \dot\theta^2 + ( R + L \, \sin\theta )^2 \; \Omega^2 \right] \\ V &= -mgL \, \cos\theta \end{align*} and the Euler-Lagrange equation for $\theta(t)$ take the form \begin{align*} m\, L^2\, \ddot\theta(t) = \frac{d}{dt} \frac{\partial \mathcal L}{ \partial \dot\theta } = \frac{\partial \mathcal L}{ \partial \theta } = m\, \Omega^2 \; ( R+L \, \sin\theta ) \: \cos\theta - mgL \: \sin\theta \end{align*} We introduce
- the eigenfrequency of the hanging arm, $\omega = \sqrt{ g/L }$
- the ratio of frequencies, $\tau = \Omega/\omega$
- the ratio of the length of the arms, $\lambda = R/L$
and absorb $\omega$ into the dimensionless time scale. Thus, we find \begin{align*} \ddot\theta = \tau^2 \; (\lambda + \sin\theta ) \: \cos\theta - \sin\theta \end{align*} which admits a conserved energy-like quantity \begin{align*} \mathcal E &= \frac{\dot\theta^2}{2} + U_{\rm eff}(\theta) \end{align*} with an effective potential \begin{align} U_{\rm eff}(\theta) &= - \frac{\tau^2}{2} \: \left( \lambda + \sin\theta \right)^2 - \cos\theta \tag{6.3.7} \end{align} The left panel of Figure 6.14 shows the effective potential for a fixed ratio $L/R=4$ and different values of $\Omega/\omega$. For small frequencies, $\Omega/\omega = 0.2$, the masses are pushed outwards such that the equilibrium position is no longer at $\theta = 0$. Otherwise, the phase space plot looks like the one of a mathematical pendulum. For increasing $\tau = \Omega/\omega$ a shoulder emerges in the potential, and for $\tau > \tau_c \simeq 1.5$ this leads to the emergence of a new minimum with $-\pi/2<\theta_-<0$. It is separated from the previous minimum by a maximum at $\theta_+$ with $-\theta_- \gg -\theta_+ > 0$. For $\tau > \tau_c$ there are two stable fixed points that lie in regions surrounded by homoclinic trajectories that start and end at $\theta_+$. Further outside there are oscillating trajectories that move around both fixed points, and beyond the heteroclinic trajectories that connect the maxima of the potential one finds trajectories that keep rotating in the same direction.
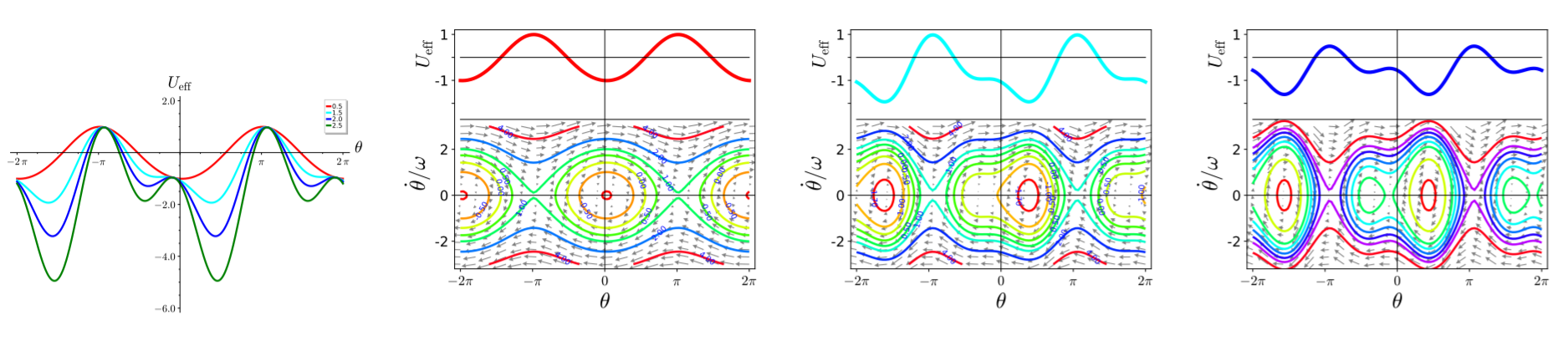 Figure 6.14: The effective potential (left) and phase space plots for the parameter values
$L=4R$ and $\Omega/\omega = 0.5$, $1.5$ and $2.0$ (from left to right).
Figure 6.14: The effective potential (left) and phase space plots for the parameter values
$L=4R$ and $\Omega/\omega = 0.5$, $1.5$ and $2.0$ (from left to right).
When increasing the rotation frequency beyond $\tau_c$ a second stable solution emerges in the system. To find the parameters where it emerges we observe that fixed points emerge at positions $\theta$ where the effective force vanishes \begin{align*} \sin\theta &= \tau^2 \; \left( \lambda + \sin\theta \right) \; \cos\theta \\ \Rightarrow\quad \lambda_\tau(\theta) &= \frac{ \tan\theta }{\tau^2} - \sin\theta \end{align*} This equation is solved for a unique angle $\theta_c$ when $\lambda_\tau(\theta)$ is monotonic, and potential extrema of $\lambda_\tau(\theta)$ must fulfill \begin{align*} 0 &= \frac{d \lambda}{d \theta} = \frac{1}{\tau^2} \; \frac{1}{\cos^2\theta_c} - \cos\theta_c \qquad \Rightarrow\qquad \cos\theta_c = \tau^{-2/3} \end{align*}
Consequently,
- for $\tau<1$ the function $\lambda_\tau(\theta)$ is monotonous such that there is a unique fixed point. It is a minimum.
- for $\tau>1$ the function $\lambda_\tau(\theta)$ has a maximum and a minimum such that there can be up to three fixed point: two minima and a maximum.
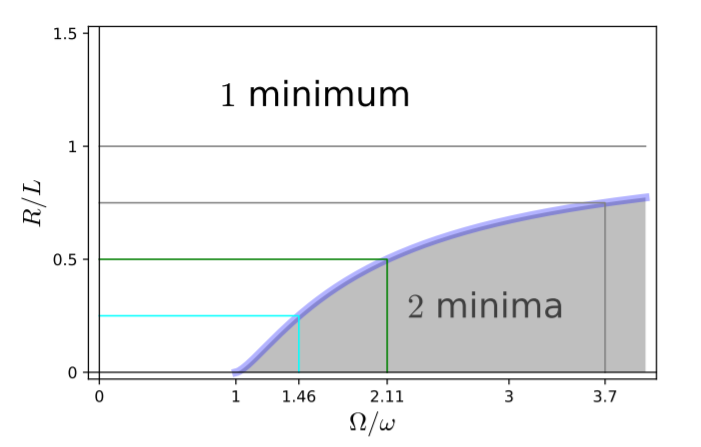
The range values $\lambda = R/L$ where there are two minima is bounded by the extrema $\lambda_\tau(\theta_c)$, \begin{align*} \lambda_c (\theta_c) &= \sin\theta_c \; \left( \frac{1}{\tau^2 \, \cos\theta_c} - 1 \right) = \mp \sqrt{1-\cos^2\theta_c }\; \left( \frac{1}{\tau^2 \, \cos\theta_c} - 1 \right) \\ &= \pm \left( 1 - \tau^{-4/3} \right)^{3/2} \end{align*} Hence, there is a single maximum for $\tau = \Omega/\omega < 1$ and when $R/L > \left( 1 - \tau^{-4/3} \right)^{3/2}$ for $\tau > 1$. In Figure 6.15 this conclusion is visualized in a phase diagram where this aspect of the behaviour is marked in the parameter plane of the problem, i.e., as function of $\tau = \Omega/\omega$ and $\lambda=R/L$.
Definition 6.8: Phase Diagram
A phase diagram for some property of a dynamics is a plot
that shows for which parameters this property can be observed.
It is illuminating to observe that the motion of the pearl on the rotating ring is recovered as the special case $R=0$ of the carousel dynamics. For $\lambda = 0$ the effective potential, Equation 6.3.7, has three critical points for $\tau > 1$, and two of them disappear in a pitchfork bifurcation when they all meet at $\theta=0$ for $\tau = 1$. In terms of the condition on the forces this happens when at $\theta=0$ the slope of $\tau^2 \: \sin\theta$ becomes larger than the one of $\tan\theta$. For $\tau > 0$ there will be three intersections of the two functions rather than a single one. The scenario for $\lambda > 0$ is different. This is most easily seen by considering a value $\tau > 1$ and increasing $\lambda$. For $\lambda=0$ there are intersections of $\tau^2 \: \sin\theta$ and $\tan\theta$ at $\theta \in \{0, \pm\theta_c\}$. Increasing $\lambda$ amounts to a vertical displacement of the sine function. The critical points that are initially at $\pm\theta_c$ will then move right and the one in the middle moves to the left because $\lambda + \sin\theta > 0$ for $\lambda>0$ and $\theta=0$. Therefore, the minimum to the right will persist, and the minimum to the left will at some point merge with the maximum and they will annihilate. Such a scenario is called a saddle-node bifurcation.
Definition 6.9: Saddle-node bifurcation
We consider a one-dimensional ODE for a real variable $x$
that depends on a parameter $p$.
In a certain range of parameters $p \in \mathbb U$ the systems has a stable fixed point at $x_s$ and an unstable fixed point at $x_u$.
A saddle-node bifurcations emerges at $p_* \in \partial \mathbb U$
when $x_u(p)$ and $x_s(p)$ meet and annihilate at
$x_* = x_u(p_*) = x_x(p_*)$.
Remark 6.8. In classical mechanics a saddle-node bifurcation emerges when the height difference between a minimum and a neighboring maximum of a potential diminishes, becomes zero in a saddle point, and subsequently, the potential will no longer have no critical point in the considered region.
6.3.5 Self Test
Problem 6.6: Basis vectors for spherical coordinates
a) Verify by explicit calculation that
$\hat{\mathbf R}$, $\hat{\boldsymbol\theta}$, and $\hat{\boldsymbol\phi}$ obey the relations
\begin{align*}
\hat{\boldsymbol\theta} = \frac{\partial \hat{\mathbf R}}{\partial \theta}
\qquad\text{ and }\qquad
\hat{\boldsymbol\phi} = \hat{\mathbf R} \times \hat{\boldsymbol\theta} \, ,
\end{align*}
and that they form an orthonormal basis.
b) How is $\hat{\boldsymbol\phi}$ related to $\partial\hat{\mathbf R} / \partial\phi$?
c) Verify also the other expressions, Equation 6.3.3, for the partial derivatives of the basis vectors.
Problem 6.7: Phase-space analysis for a pearl on a rotating ring
- Evaluate $\dot{\mathbf x} (t) = L \: \dot{\hat{\mathbf R}}(\theta(t), \Omega t )$ based on the relations established in Problem 6.6.
- Determine the kinetic energy $T$ and the potential energy $V$ of the pearl.
- Fill in the steps in the derivation of the EOM for $\theta$, as provided in Equation 6.3.4.
- Verify that neither the energy nor any of the coordinates of momentum and angular momentum are conserved for this motion.
Problem 6.8: An EOM with a subcritical pitchfork bifurcation
Consider the equation of motion
\begin{align*}
\ddot x = x \: \Bigl( x^2 - 1 \Bigr) \: \Bigl( x^2 - a \Bigr)
\end{align*}
where the right-hand side is considered as a dimensionless force on a particle
that resides at the dimensionless position $x \in \mathbb R$.
The dynamics depends on the parameter $a \in \mathbb R$.
- Determine the fixed points of the dynamics, and verify that $x=0$ is a stable fixed point for $a<0$ and an unstable fixed point for $a>0$.
- Verify that the dynamics has a subcritical pitchfork bifurcation at $a=0$.
- Sketch the bifurcation diagram, i.e. a plot analogous to Figure 6.10 where the positions of the fixed points are indicated as function of $a$. Use solid lines for stable fixed points and dotted lines for unstable fixed points.
- Sketch the form of the potential for dynamics with $a<0$, $0<a<1$, and $a>1$.
Problem 6.9: An EOM with a saddle-node bifurcation
Consider the equation of motion
\begin{align*}
\ddot x = (1-x) \: \Bigl( x^2 + a \Bigr)
\end{align*}
where the right-hand side is considered as a dimensionless force on a particle
that resides at the dimensionless position $x \in \mathbb R$.
The dynamics depends on the parameter $a \in \mathbb R$.
- Determine the fixed points of the dynamics, and verify that the EOM has three fixed points for $a<0$, two fixed points for $a=1$, and a single fixed point for $a<0$.
- Sketch the bifurcation diagram, i.e. a plot analogous to Figure 6.10 where the positions of the fixed points are indicated as function of $a$. Use solid lines for stable fixed points and dotted lines for unstable fixed points.
- Sketch the form of the potential for dynamics with $a<-1$, $-1<a<0$, and $a>0$.