4.9 Solving ODEs by coordinate transformations: Kepler's 1st law
In polar coordinates $\mathbf R = (R,\theta)$ the kinetic energy takes the form $\mu \dot{\mathbf R}^2 / 2 = \mu \, \bigl( \dot R^2 + (R \dot\theta)^2 \bigr)/2$ while the conservation of angular momentum implies $R \dot\theta = L / (\mu R)$ with $L = |\mathbf L|$. Consequently, \begin{align} E = \frac{\mu}{2} \: \dot R^2(t) + \frac{ L^2 }{2\mu \, R^2(t)} - \frac{ m_1 m_2 G }{R(t)} \tag{4.9.1} \end{align}
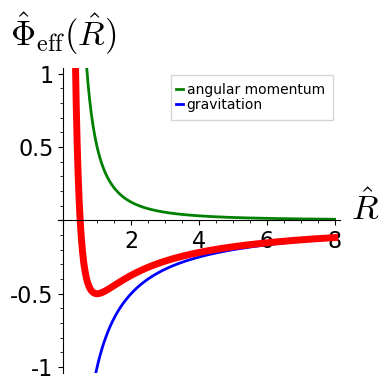 Figure 4.15: Effective potential $\hat\Phi = \Phi\,R_0 / m_1 \, m_2 \, G$
for the Kepler problem as function of the dimensionless distance
$\hat R = R / R_0$,
where $R_0 = L^2 / \mu \, m_1 \, m_2 \, G$.
Figure 4.15: Effective potential $\hat\Phi = \Phi\,R_0 / m_1 \, m_2 \, G$
for the Kepler problem as function of the dimensionless distance
$\hat R = R / R_0$,
where $R_0 = L^2 / \mu \, m_1 \, m_2 \, G$.
which is equivalent to the motion of a particle of mass $\mu$ at position $R$ in the one-dimensional effective potential (Figure 4.15) \begin{align*} \Phi_{\text{eff}}( R ) = \frac{ L^2 }{2\mu \, R^2} - \frac{ m_1 m_2 G }{R} \, . \end{align*}
The first, repulsive contribution to the effective potential arises from angular momentum conservation, and the second, attractive contribution is due to gravity. There is no elementary way to determine the function $R(t)$. However, based on Equation 4.9.1 one can plot the trajectories in phase space, $\dot R ( R )$ for different energies. This plot is provided in Figure 4.16. For negative energies there are bounded trajectories that oscillate in the minimum of the potential $\Phi_{\text{eff}}$. For zero energy the trajectory reaches till $R = \infty$, and reaches infinity with zero speed. For a positive energy the trajectory reaches till $R = \infty$, and it will go there with speed $\dot R = \sqrt{2E / \mu}$. However, one can determine the shape $R(\theta)$ of the trajectories by observing \begin{align*} \dot R(\theta) = \dot\theta \: \frac{\mathrm{d} R(\theta)}{\mathrm{d} \theta} = \frac{L}{\mu \, R^2} \: R'(\theta) \end{align*}
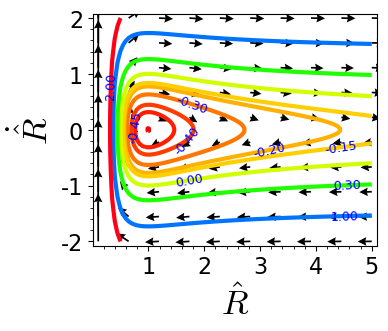 Figure 4.16: The phase-space flow for the EOM of $R(t)$ provided by Equation 4.9.1.
The plot adopts dimensionless units with length scale $R_0$ introduced in Figure 4.15
and a time scale $t_0 = \sqrt{ \mu \, R_0^3 / m_1\, m_2\, G }$.
Solid lines refer to solutions for different dimensionless energy,
with values marked on the contour lines.
Figure 4.16: The phase-space flow for the EOM of $R(t)$ provided by Equation 4.9.1.
The plot adopts dimensionless units with length scale $R_0$ introduced in Figure 4.15
and a time scale $t_0 = \sqrt{ \mu \, R_0^3 / m_1\, m_2\, G }$.
Solid lines refer to solutions for different dimensionless energy,
with values marked on the contour lines.
such that \begin{align*} E = \frac{L^2}{2\, \mu} \: \left( \frac{ R'^2 }{ R^4 } + \frac{1}{ R^2 } \right) - \frac{ m_1 \, m_2 \, G }{ R } \end{align*} In terms of $w(\theta) = 1/ R(\theta)$ this implies
\begin{align} \frac{\mu \, E}{L^2} &= \frac{1}{2} \: \bigl( w'(\theta) \bigr)^2 + \frac{1}{2} \: w^2(\theta) - \frac{ m_1 \, m_2 \, \mu \, G}{L^2} \: w(\theta) \tag{4.9.2} \end{align} and differentiating with respect to $\theta$ provides \begin{align*} 0 = w'(\theta) \; \left[ w''(\theta) + w(\theta) - \frac{m_1\, m_2 \, \mu \, G}{L^2} \right] \, . \end{align*} The expression in the square bracket is a second order linear ODE with solution \begin{align*} w(\theta) = \frac{ \mu \, m_1 \, m_2\, G}{L^2} \; \left[ 1 + \epsilon \; \cos\left( \theta - \theta_0 \right) \right] \end{align*} where $\epsilon$ and $\theta_0$ are integration constants that must be determined from the initial conditions. Inserting $w(\theta)$ into Equation 4.9.2 yields \begin{align*} \frac{\mu \, E}{L^2} = \frac{\epsilon^2 - 1}{2} \; \left( \frac{m_1 \, m_2 \, \mu \, G}{L^2} \right)^2 \quad \Rightarrow \quad \epsilon^2 = 1 + \frac{ 2 \, E \: L^2 }{ \mu \; \left( m_1\, m_2\, G \right)^2 } \end{align*} Hence, $\epsilon$ is fully determined by the parameters and the conservation laws of the Kepler problem, while $\theta_0$ determines the orientation of the trajectory in the plane. Commonly, one chooses the coordinate frame where $\theta_0 = 0$. For the motion of a planet around the sun this entails
Theorem 4.4 Kepler's first law
The trajectories of planets around the sun
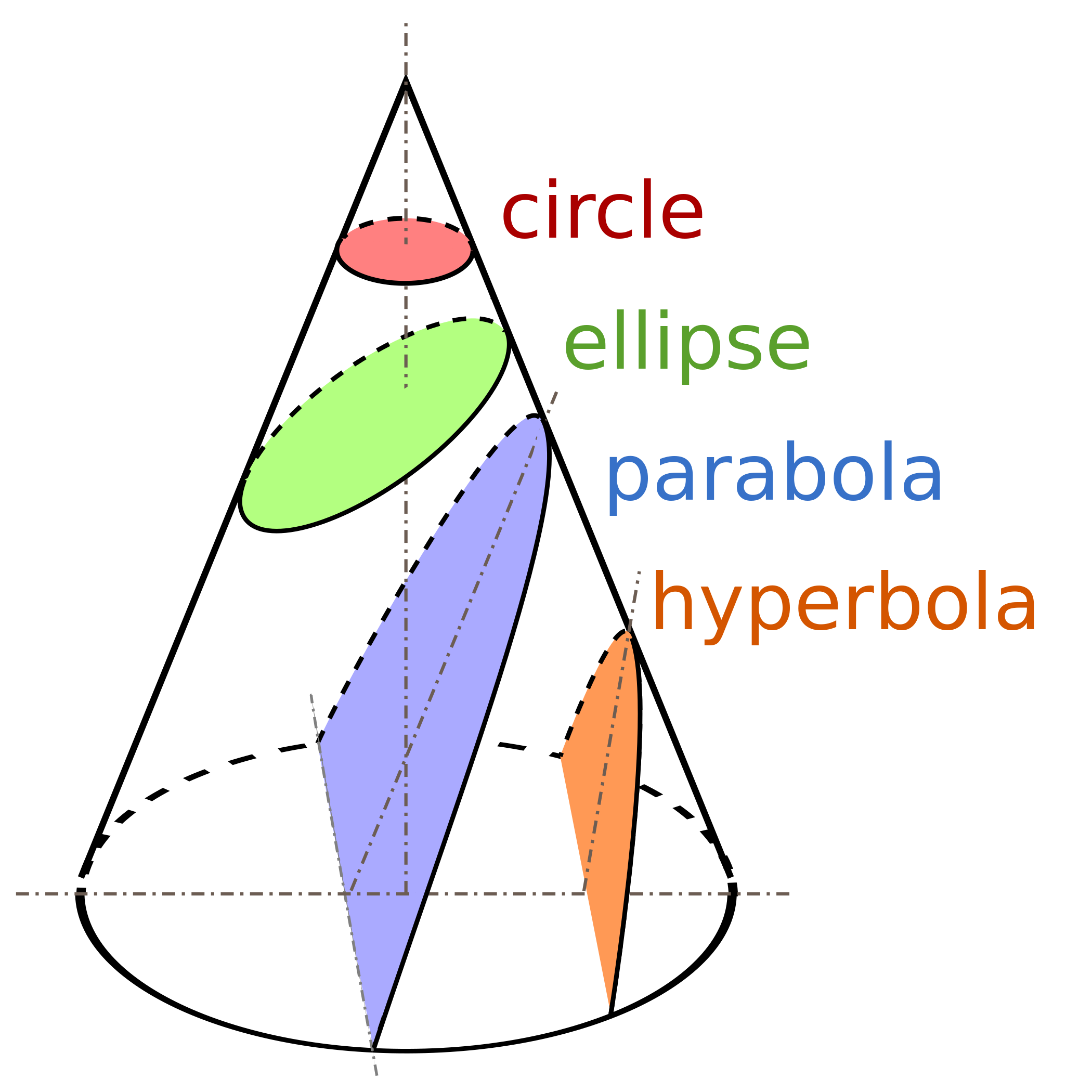
are described by sections of the cone with a plane,\
\begin{align}
R(\theta) = \frac{ R_0 }{ 1 + \epsilon \, \cos( \theta - \theta_0 ) } \tag{4.9.3}
\end{align}
where $R_0 = L^2 / m_1\, m_2\, \mu \, G$ sets the length scale of the trajectory and $\theta_0$ the orientation in the plane.
The parameter $\epsilon$ sets its shape:
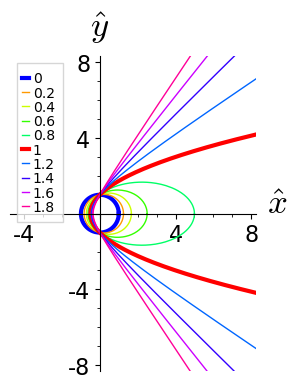
for $\epsilon = 0$ the shape amounts to a circle with radius$R_0$,
for $0 < \epsilon < 1$ to an ellipse,
for $\epsilon = 1$ to a parabola,
and for $\epsilon > 1$ to a hyperbola.
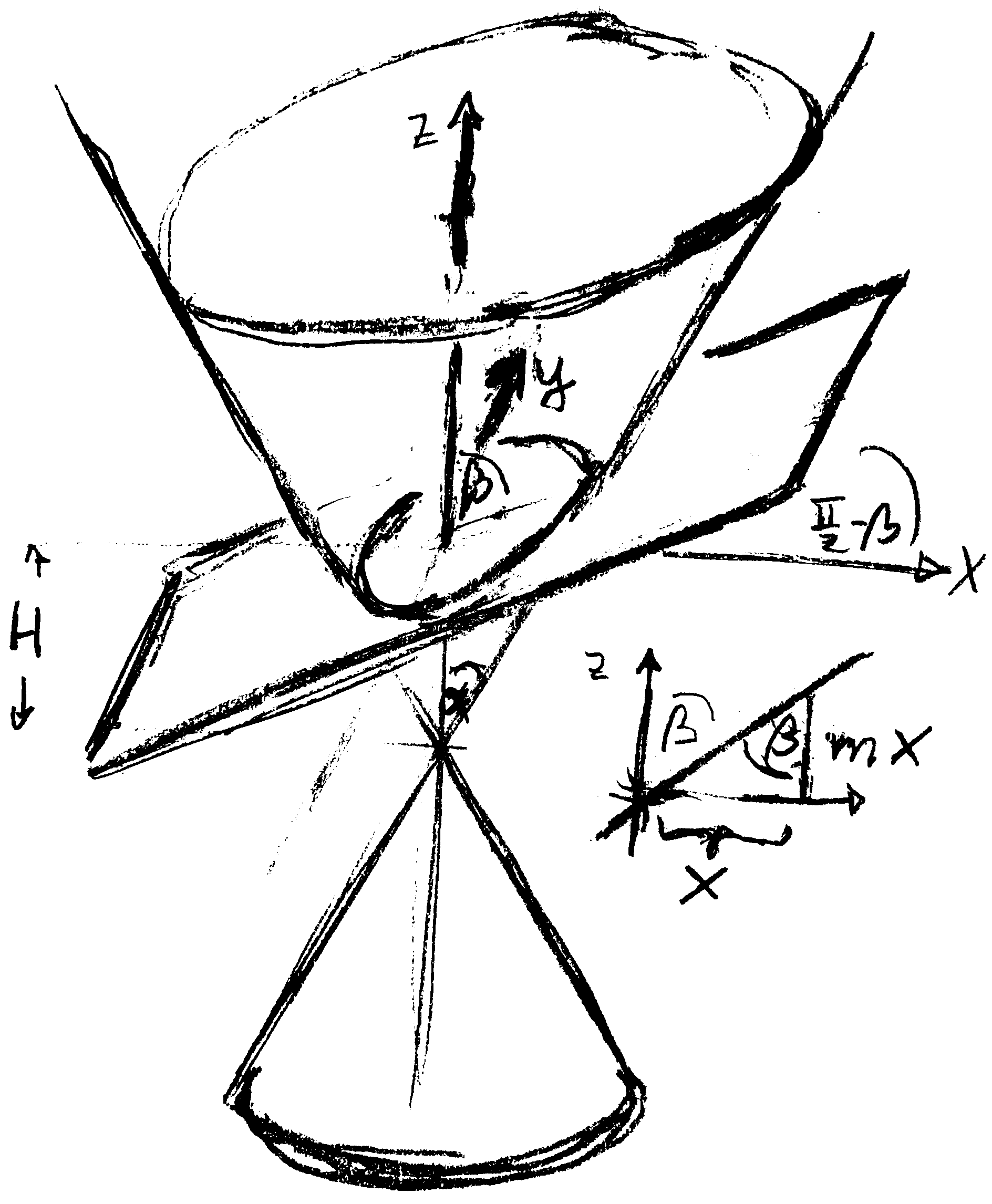 Figure 4.17: Section of a cone double and a plane.
The axis are drawn here at the intersection point of the plane with the cone axis,
in order to emphasize the the plane is tilted around the $y$ axis.
For calculations in the main text the vertex of the cone will be chosen as origin of the coordinate system.
Figure 4.17: Section of a cone double and a plane.
The axis are drawn here at the intersection point of the plane with the cone axis,
in order to emphasize the the plane is tilted around the $y$ axis.
For calculations in the main text the vertex of the cone will be chosen as origin of the coordinate system.
Proof. We consider the section of a cone with opening angle $\alpha$ and its symmetry axis aligned along the $z$-axis, and a plane, as sketched in Figure 4.17. The origin of the coordinate system is a the vertex of the cone. The plane is tilted with respect to the $y$-axis such that it forms an angle $\beta$ with the $z$-axis, and it intersects the $z$-axis at height $H$. The points in the plane have coordinates \begin{align*} \mathbf q = \begin{pmatrix} x \\ y \\ H + m\, H \end{pmatrix} \qquad \text{with} \quad m^{-1} = \tan\beta \end{align*} The point $\mathbf q$ lies on the cone when $ \mathbf q \cdot \hat{\boldsymbol z} = \left\lvert \mathbf q \right\rvert \: \cos\alpha$, which entails \begin{align*} \left( H + m\, x \right)^2 = \cos^2\alpha \; \left( x^2 + y^2 + (H+m\,x)^2 \right) \end{align*} Henceforth, we adopt dimensionless coordinates $\hat x = x/H\, \tan\alpha$ and $\hat y = y/ H \tan\alpha$, and we introduce the abbreviation $\epsilon = m \, \tan\alpha$. We will denote the distance from the origin in the $(x,y)$-plane as $R = \sqrt{ \hat x^2 + \hat y^2}$, and introduce $\theta$ such that $\hat x = R \, \cos\theta$. This entails \begin{align*} \left( 1 + \epsilon \, R \, \cos\theta \right)^2 = R^2 \end{align*} with solutions \begin{align*} R_\pm &= \frac{ \epsilon \, \cos\theta }{ 1 - \epsilon^2 \, \cos^2\theta } \pm \frac{ \left[ \epsilon^2 \, \cos^2\theta + \left( 1 - \epsilon^2 \, \cos^2\theta \right) \right]^{1/2} }{ 1 - \epsilon^2 \, \cos^2\theta } \\ &= \frac{ \epsilon \, \cos\theta \pm 1 }{ 1 - \epsilon^2 \, \cos^2\theta } = \frac{ -1 }{ \pm 1 + \epsilon \, \cos\theta } \end{align*} Hence, Equation 4.9.3 describes a cone section with length scale $R_0 = H \, \tan\alpha$ and eccentricity $\epsilon = m \, \tan\alpha$.
 \\Magister Mathematicae/wikimedia,
CC BY-SA 3.0
Figure 4.18: Shape of conic sections for parameters,
$\epsilon=0$ circle,
$0<\epsilon<1$ ellipse,
$\epsilon=1$ parabola, and
$\epsilon>1$ hyperbola.
\\Magister Mathematicae/wikimedia,
CC BY-SA 3.0
Figure 4.18: Shape of conic sections for parameters,
$\epsilon=0$ circle,
$0<\epsilon<1$ ellipse,
$\epsilon=1$ parabola, and
$\epsilon>1$ hyperbola.
The eccentricity amounts to the ratio of the slope $m$ of the $z$ coordinates of points in the plane as function of $x$,
and the slope $1/\tan\alpha$ of the line obtained as intersection of the double cone and the $(x,z)$ plane.
This ratio determines the shape of the conic section (see Figure 4.18).
For $\epsilon = 0$ the shape is a circle $R^2 = 1$.
For $\epsilon = 1$ the shape is a parabola described by $1 + 2 \, \epsilon \, \hat x = \hat y^2$.
For $0 < \epsilon < 1$ the shape is an ellipse described by
\begin{align*}
\frac{ 1+\epsilon^2 }{ 1-\epsilon^2 } = \hat y^2 + \left( 1-\epsilon^2 \right) \; \left( \hat x - \frac{\epsilon}{1-\epsilon^2} \right)^2
\end{align*}
For $1 < \epsilon$ the shape is a hyperbola described by
\begin{align*}
\hat y = \pm \sqrt{ \frac{ -1 }{ \epsilon^2 - 1 } + \left( \epsilon^2 - 1 \right) \; \left( \hat x + \frac{\epsilon}{\epsilon^2 - 1} \right)^2 }
\end{align*}
qed
4.9.1 Self Test
Problem 4.20: Keeping the Moon at a distance
Something goes wrong at the farewell party for the settlers of the new Moon colony
Sleeping Beauty 1
such that an extremely annoyed evil fairy switches off gravity for the Moon.
Luckily there also is a good fairy at the party.
She cannot undo the curse but offers to strip all protons from all water-molecules in a bucket of water
that you give to her, and hide them on Moon.
The Coulomb attraction between electrons on Earth and protons on Moon can then undo the damage.
- How much water would you give to her?
- What will happen to the Earth-Moon system when you are off by $20%$ by a factor of two, or even by an order of magnitude? Hint:
Problem 4.21:
Mechanical similarity and dimensional analysis
We discuss here the relation between dimensional analysis,
introduced in Section 1.2,
and mechanical similarity,
adopting the notations introduced in the beginning of section 4.8.
a) We consider a system with kinetic energy $T = \frac{1}{2} \, \sum_i m_i \, \dot{\mathbf q}_i^2$, and consider a potential that admits the following scaling \begin{align*} V' = \mu^\alpha \, \lambda^\beta \: V \end{align*} Show that the EOM are then invariant when one rescales time as \begin{align*} \tau = \mu^{(1-\alpha)/2} \, \lambda^{(2-\beta)/2} \end{align*}
b) Consider now two pendulums, $V=mgz$ with different masses and length of the pendulum arms.
Which factors $\tau$, $\lambda$, and $\mu$ relate their trajectories?
How will the periods of the pendulums thus be related to the ratio of the mass and the length of the arms?
Which scaling do you expect based on a dimensional analysis?
c) What do you find for the according discussion of the periods of a mass subjected to a harmonic force,
$V = k \, |\mathbf q|^2 / 2$?
d) Discuss the period of the trajectories in the Kepler problem, $V = mMG/|\mathbf q|$. In this case the dimensional analysis is tricky because the masses of the sun and of the planet appear in the problem. What does the similarity analysis reveal about the relevance of the mass of the planet for Kepler's third law?
Problem 4.22:
Conic Sections
In the margin we show the shape of conic sections for different eccentricity $\epsilon$.
- Show that all conic sections intersect the $\hat y$ axis at $\pm 1$.
- Show that the conic sections intersect the $\hat x$ axis at $-1 / (\epsilon \pm 1)$. Where are these points located for different conic sections?
- How does Equation 4.9.1 look like after introducing the dimensionless units adopted in Figure 4.15, Figure 4.16? Write down the solution of the EOM in dimensionless units.
- Find an alternative choice of the length scale such that all trajectories intersect the $x$-axis at the potion $-1$, and prepare the corresponding plot of the trajectory shapes in the $(x,y)$-plane.