4.8 Mechanical similarity -- Kepler's 3rd Law
Two solutions of a differential equations are called similar when they can be transformed into one another by a rescaling of the time-, length-, and mass-scales. We indicate the rescaled quantities by a prime, and denote the scale factors as $\tau$, $\lambda$, and$\alpha$, respectively, \begin{align*} t' = \tau t \, , \qquad\qquad \mathbf q_i ' = \lambda \mathbf q_i \, , \qquad\qquad m_i ' = \alpha m_i \end{align*} We explore the consequences of this idea for the Kepler problem, i.e., for two point particles interacting by a gravitation force $\mathbf F$ deriving from the following potential \begin{align*} \Phi( |\mathbf R| ) = \frac{ m_1 m_2 G }{ | \mathbf R | } \quad \Rightarrow \quad \mathbf F = -\nabla \Phi( |\mathbf R| ) = \frac{ m_1 m_2 G }{ | \mathbf R |^3 } \; \mathbf R \end{align*}
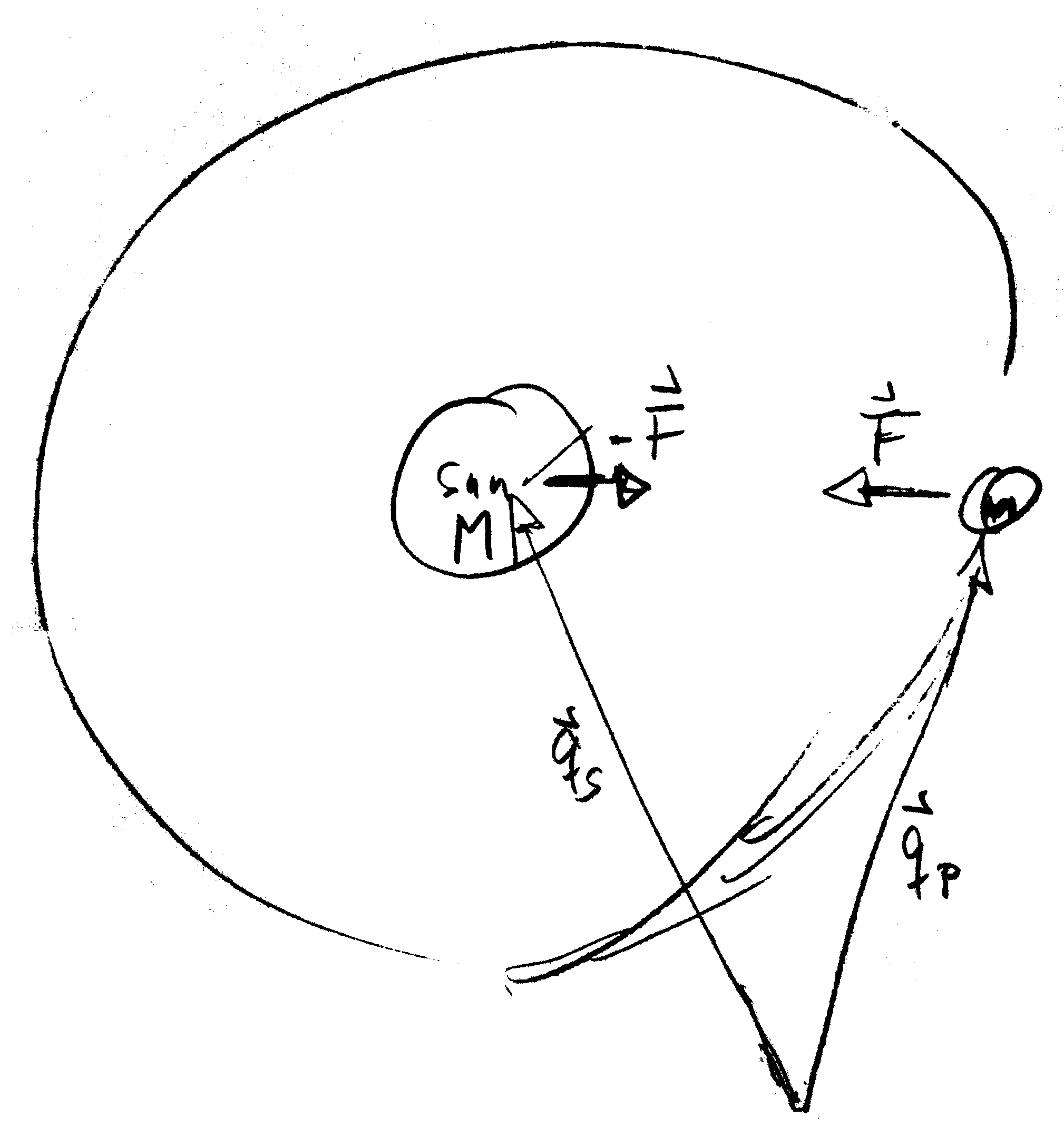 Figure 4.14: Setup of and notations for the motion of a planet around the sun.
Here $m_S$ and $m_P$ are the mass of the sun and the planet, respectively,
and $\mathbf q_S$ and $\mathbf q_P$ are their positions.
The relative position is $\mathbf R = \mathbf q_P - \mathbf q_S$.
Figure 4.14: Setup of and notations for the motion of a planet around the sun.
Here $m_S$ and $m_P$ are the mass of the sun and the planet, respectively,
and $\mathbf q_S$ and $\mathbf q_P$ are their positions.
The relative position is $\mathbf R = \mathbf q_P - \mathbf q_S$.
The setup for a planet going around the sun is sketched in Figure 4.14. acting on the planet and pointing towards the sun. We only consider the relative motion and assume that there are no other forces acting on the sun and the planet. Information about the period and the shape of the trajectory is obtained from the energy for the relative motion \begin{align*} E = \frac{\mu}{2} \: \dot{\mathbf R}^2 + \Phi( |\mathbf R| ) \end{align*} This energy is conserved because \begin{align*} \frac{\mathrm{d} E}{\mathrm{d} t} &= \frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{\mu}{2} \: \dot{\mathbf R}^2 + \Phi( |\mathbf R| ) \right) = \mu \: \dot{\mathbf R} \cdot \ddot{\mathbf R} + \dot{\mathbf R} \cdot \nabla\Phi( |\mathbf R| ) \\ &= \dot{\mathbf R} \: \cdot \left( \mu\, \ddot{\mathbf R} - \mathbf F \right) = \mathbf 0 \end{align*} Here, we used that $\mathbf F = \mu \, \ddot{\mathbf R}$. In our planetary system the trajectories of the planets are all circular to a good approximation. They are therefore described by the same solution of the EOM up to a rescaling of the length scale and the time scale. The former accounts to their different distance to the Sun, and the latter to the different periods of their motion. We observe now that $\mu = m_1 \, m_2 / (m_1+m_2)$ and that the Sun mass $m_S$ is $1000$ times larger than the mass of Jupiter, the largest planet. Therefore, for the motion of the planets we have $m_1\:m_2/\mu = m_1+m_2 \simeq m_S$, and \begin{align*} \frac{ E }{\mu} \simeq \frac{ \dot{\mathbf R}^2 }{2} + \frac{ m_S \, G }{ \lvert R \rvert } \end{align*} We expect that different planets follow the same trajectory up to rescaling space and time units, and a different constant value of their energy. We hence explore the consequences of the scaling $\lambda \mathbf R(t)$ and $\tau t$ \begin{align*} \frac{ E }{\mu} \simeq \frac{\lambda^2}{\tau^2} \frac{ \dot{\mathbf R}^2 }{2} + \frac{1}{\lambda} \frac{ m_S \, G }{ \lvert R \rvert } \\ \Leftrightarrow \frac{ E }{\mu} \frac{\tau^2}{\lambda^2} \simeq \frac{ \dot{\mathbf R}^2 }{2} + \frac{\tau^2}{\lambda^3} \frac{ m_S \, G }{ \lvert R \rvert } \end{align*} where the right-hand side remains invariant iff $\tau^2/\lambda^3 = \text{const}$. This entails
Theorem 4.3 Kepler's third law
The square of the period $T$ of the planets in our planetary system are proportional
to the third power of their distance $D$ to the sun.
