Table of Contents
6.5 Dynamics of 2-particle systems
In Section 6.3 and Section 6.4 we discussed the motion of single particles whose motion is constraint by tracks, arms and joints. Now we revisit the treatment of the Kepler problem, Section 4.6, in order to explore settings with two interacting particles. The central idea in this endeavor is a representation of the particle position as a sum of the position of the center of mass $\mathbf Q$ and the relative coordinate $\mathbf R$.
6.5.1 The Kepler problem revisited
We consider two celestial bodies with masses $m_1$ and $m_2$ that reside at the positions $\mathbf x_1$ and $\mathbf x_2$ in 3D space. The bodies are modeled as point particles that interact by gravity, (cf. Example 4.10), \begin{align*} T &= \frac{m_1}{2}\: \dot{\mathbf x}_1^2 + \frac{m_2}{2}\: \dot{\mathbf x}_2^2 \\ V &= -\frac{ m_1 m_2 G }{ \lvert \mathbf x_2 - \mathbf x_1 \rvert } \end{align*} The positions $(\mathbf x_1, \mathbf x_2)$ of the two bodies are coordinates in a 6D vector space. Prior to calculating EOMs it is advisable to look for characteristic properties of the dynamics that will simplify the treatment of the dynamics of the 6DOF system. Here, the potential energy only depends on $\mathbf R = \mathbf x_2 - \mathbf x_1$. This suggests to adopt a different basis that allows us to express the dynamics in terms of $\mathbf R$ and another position $\mathbf Q = a_1 \, \mathbf x_1 + a_2 \, \mathbf x_2$ that is linearly independent of $\mathbf R$. In that case $\mathbf Q$ will be cyclic, and it can be dealt with by a conservation law. We observe that \begin{align*} \mathbf x_1 & = ( \mathbf Q + a_2 \, \mathbf R ) / (a_1+a_2) \\ \mathbf x_2 &= ( \mathbf Q - a_1 \, \mathbf R ) / (a_1+a_2) \end{align*} such that \begin{align*} T &= \frac{1}{2} \: \dot{\mathbf Q}^2 \: \left( \frac{m_1 + m_2}{(a_1+a_2)^2} \right) + \dot{\mathbf Q} \cdot \dot{\mathbf R} \: \left( \frac{m_1\, a_2 - m_2\, a_1}{(a_1+a_2)^2} \right) + \frac{1}{2} \: \dot{\mathbf R}^2 \: \left( \frac{m_1\,a_2^2 + m_2\,a_1^2}{(a_1+a_2)^2} \right) \end{align*} For $a_i \propto m_i$, $i\in\{1,2\}$ the mixed term vanishes, and the $\mathbf R$ dynamics is not coupled to the $\mathbf Q$ dynamics. To avoid clutter in the equations we pick $a_i = m_i/(m_1+m_2)$ such that $a_1+a_2 = 1$ such that \begin{align*} \mathbf Q = \frac{\sum_i m_i \, x_i }{\sum_i m_i } \end{align*} Hence, $\mathbf Q$ is the center of mass of the two-body system. Further we introduce the total mass $M$ and the reduced mass $\mu$, \begin{align*} M &= m_1 + m_2 \\ \mu &= m_1\,a_2^2 + m_2\,a_1^2 = \frac{m_1\,m_2^2 + m_2\, m_1^2}{(m_1+m_2)^2} = \frac{m_1\,m_2}{m_1+m_2} \end{align*} This provides \begin{align} \nonumber T &= \frac{M}{2} \: \dot{\mathbf Q}^2 + \frac{\mu}{2} \: \dot{\mathbf R}^2 \\ \nonumber V &= -\frac{ \mu M G }{ \lvert \mathbf R \rvert } \\ \mathcal L &= T-V = \frac{M}{2} \: \dot{\mathbf Q}^2 + \frac{\mu}{2} \: \dot{\mathbf R}^2 + \frac{ \mu M G }{ \lvert \mathbf R \rvert } \tag{6.5.1} \end{align} The generalization to more than two particles is addressed in Problem 6.14.
Equation 6.5.1 asserts that $\mathbf Q$ is a cyclic variable. I provides the conservation law \begin{align*} 0 = \frac{\mathrm{d}}{\mathrm{d} t} \mathbf P \quad\text{with}\quad \mathbf P = M \: \dot{\mathbf Q} = \sum_i m_i \: \dot{\mathbf x}_i \end{align*} and the center-of-mass motion \begin{align*} \mathbf Q(t) = \mathbf Q(t_0) + \dot{\mathbf Q}(t_0) \: (t-t_0) \, . \end{align*} In the discussion of the harmonic oscillator, Section 6.4.3, we observed that the angular momentum is conserved when the potential is rotationally invariant. Hence, we adopt cylindrical coordinates $(R,\theta,z)$ where $\mathbf R(t_0)$ and $\dot{\mathbf R}(t_0)$ have vanishing $z$-coordinates, \begin{align*} \mathcal L - \frac{M}{2} \: \dot{\mathbf Q}^2 &= \frac{\mu}{2} \: \Bigl( \dot z^2 + \dot R^2 + R^2 \; \dot\theta^2 \Bigr) + \frac{ \mu M G }{ R } \end{align*} Here, $z$ is a cyclic variable and for the specified initial conditions it vanishes for all times, \begin{align*} \ddot z = 0 \quad \Rightarrow \quad z(t) = z(t_0) + \dot z(t_0) \: (z-z_0) = 0 \, . \end{align*} Moreover, also $\theta$ is a cyclic variable. It provides the conservation law \begin{align*} 0 &= \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial \dot\theta } = \frac{\mathrm{d}}{\mathrm{d} t} \bigl( \mu \, R^2 \: \dot\theta \bigr) \\ \Rightarrow C_\theta = \mu \, R^2 \: \dot\theta = \text{const}. \end{align*} Finally, there is no explicit time dependence in the kinetic and potential energy. Therefore, energy, $T+V$, must be preserved. In view of $M\, \dot{\mathbf Q}^2/2 $const and $\dot z = 0$ this implies \begin{align*} E = \frac{\mu}{2} \: \Bigl( \dot R^2 + R^2 \; \dot\theta^2 \Bigr) - \frac{ \mu M G }{ R } = \frac{\mu}{2} \: \dot R^2 + \frac{C_\theta^2}{2\,\mu \; R^2} - \frac{ \mu M G }{ R } \, . \end{align*} The solution of this equation was discussed in Section 4.9.
6.5.2 Spring on rails
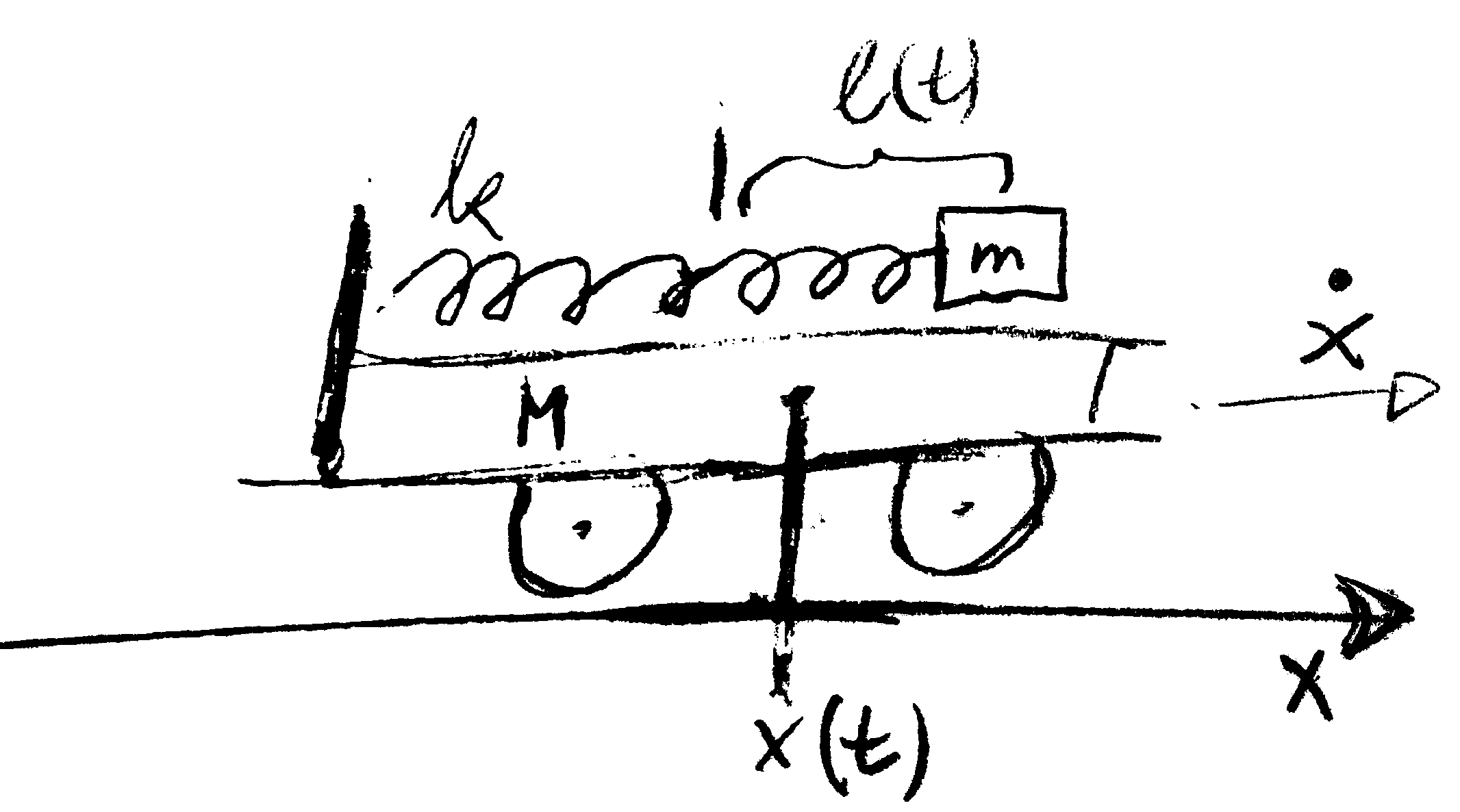 Figure 6.19: Setup of the spring on rails considered in Section 6.5.2.
Figure 6.19: Setup of the spring on rails considered in Section 6.5.2.
We consider a cart that moves without friction on a horizontal track (see Figure 6.19). It has mass $M$, and at time $t$ it is located at position $x(t)$. On the cart we attach a weight of mass $m$ to a spring with spring constant $k$. It oscillates without friction in the track direction, and its displacement from the rest position is denoted as $\ell(t)$. The kinetic energy and potential energy of the cart are \begin{align*} T_c = \frac{M}{2} \: \dot x^2 \qquad\text{ and }\qquad V_c = 0 \end{align*} Its potential energy due to gravity vanishes because the cart moves horizontally. We denote the rest position of the weight $m$ as $x(t) + e$. Hence, at time $t$ it is located at $q(t) = x(t) + e + \ell(t)$. Its kinetic energy and potential energy are \begin{align*} T_w = \frac{m}{2} \: (\dot x + \dot\ell)^2 \qquad\text{ and }\qquad V_w = 0 \end{align*} Also in this case the potential energy due to gravity vanishes because the weight moves horizontally. However, there is a contribution to the potential due to the extension of the spring, \begin{align*} V_s = \frac{k}{2} \ell^2 \end{align*} Altogether, this provides the Lagrangian: \begin{align*} \mathcal L = \frac{M}{2} \: \dot x^2 + \frac{m}{2} \: (\dot x + \dot\ell)^2 - \frac{k}{2} \ell^2 \, . \end{align*} Here, $x$ is a cyclic variable, \begin{align*} 0 = \frac{ \partial\mathcal L }{ \partial\dot x } = \frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial\mathcal L }{ \partial x } = \frac{\mathrm{d}}{\mathrm{d} t} \bigl( M \, \dot x + m \, (\dot x + \dot\ell) \bigr) \end{align*} that provides the conserved quantity \begin{align*} P = (M+m) \: \dot x + m \, \dot\ell = \frac{\mathrm{d}}{\mathrm{d} t} \left( M \, x + m \: \bigl( x + \ell \bigr) \right) = (m+M) \, Q \end{align*} where \begin{align} Q = \frac{M}{m+M} \: x + \frac{m}{m+M} \, (x+e+\ell) = x + \frac{m}{m+M} \, (e+\ell) \tag{6.5.2} \end{align} is the $x$-component of the center of mass of the system, i.e., of the cart and the weight attached to the cart. Hence, $P = (m+M) \: \dot Q$ is the momentum of the horizontal center-of-mass motion. Momentum conservation implies
\begin{align} Q(t) = Q(t_0) + \dot Q(t_0) \: (t-t_0) \tag{6.5.3} \end{align} In the following we work in the center of mass frame. Equation 6.5.2 provides \begin{align*} x &= Q - \frac{m}{m+M} \, (e+\ell) \\ \dot x &= \dot Q - \frac{m}{m+M} \, \dot\ell \end{align*} such that the Lagrangian takes the form \begin{align*} \mathcal L &= \frac{M}{2} \: \left( \dot Q - \frac{m}{m+M} \, \dot\ell \right)^2 + \frac{m}{2} \: \left( \dot Q - \frac{m}{m+M} \, \dot\ell + \dot\ell \right)^2 - \frac{k}{2} \: \ell^2 \\ &= \frac{m+M}{2} \: \dot Q^2 + \frac{2}{2} \: \left( - M \: \frac{m}{m+M} + m \: \frac{M}{m+M} \right) \dot Q \; \dot\ell \\ &+ \frac{1}{2} \: \frac{m \, M}{( m+M )^2} \bigl( m + M \bigr) \: \dot\ell^2 - \frac{k}{2} \: \ell^2 \\ &= \frac{m+M}{2} \: \dot Q^2 + \frac{1}{2} \: \frac{m \, M}{ m+M } \: \dot\ell^2 - \frac{k}{2} \: \ell^2 \end{align*} As expected by analogy to the Kepler problem the total mass $m+M$ and the reduced mass $\mu=mM/(m+M)$ appear in front of the kinetic-energy contributions of the center of mass $Q$ and the distance between the masses $\dot e + \dot\ell = \dot\ell$, respectively. There is no explicit time dependence in this problem, and $\dot Q = $const due to the momentum conservation, $P$. Hence, the energy $E$ of the relative motion is conserved, \begin{align*} E = \frac{\mu}{2} \: \dot\ell^2 + \frac{k}{2} \: \ell^2 \end{align*} This amounts to the energy of a one-dimensional harmonic oscillator with frequency $\omega = \sqrt{k/\mu}$, and time evolution \begin{align*} \ell(t) = A \: \sin\bigl( \phi + \omega \, (t-t_0) \bigr) \end{align*} where $\phi$ and $\ell_0$ are provided by the initial conditions \begin{align*} \left . \begin{aligned} \ell(t_0) &= A \: \sin\phi \\ \dot\ell(t_0) &= A \, \omega \: \cos\phi \end{aligned} \right\} \quad\Rightarrow\quad \left \{ \begin{aligned} \phi &= \arctan \frac{\omega \, \ell(t_0)}{ \dot\ell(t_0) } \\ A &= \ell(t_0) / \sin\phi \end{aligned} \right. \end{align*} Hence, the position of the cart $x(t)$ is obtained as \begin{align*} x(t) &= Q(t) - \frac{m}{m+M} \, \bigl( e + \ell(t) \bigr) \\ &= Q_0 - \frac{M \: e}{m+M} + \frac{P \: (t-t_0)}{m+M} - \frac{m}{m+M} \, A \: \sin\bigl( \phi + \omega \, (t-t_0) \bigr) \end{align*} It is illuminating to take a closer look at the motion of the system for a heavy cart, $M\ll m$, and a heavy weight, $m \ll M$. To this end we select an initial condition where the cart is at rest at the rest position of the spring initially, $Q_0=k\,M/(m+M)$. We hold the spring in a stretched position and release it at time $t_0$. Hence, also $P=0$ and $\phi = \pi/2$, and \begin{align*} x(t) &= - \frac{m}{m+M} \, A \: \cos\bigl( \omega \, (t-t_0) \bigr) \end{align*} For $M \gg m$ the cart will barely move, while the weight will oscillate with amplitude $A$ and frequency \begin{align*} \omega = \sqrt{k \: \frac{ m+M }{mM} } = \sqrt{ \frac{k}{m} \: (1+\varepsilon) } = \sqrt{ \frac{k}{m} } \; \left( 1 + \frac{\varepsilon}{2} - \frac{\varepsilon^2}{8} + \cdots \right) \end{align*} This is the eigenfrequency of the cart-weight system when the support does not move, and, indeed, it does not move because the cart is much heavier than the weight. In contrast, for $m \gg M$ the cart moves roughly with amplitude $A$, while the weight stays approximately at rest: \begin{align*} x + e + \ell &= e + \left( 1 - \frac{m}{m+M} \right) \, A \: \cos\bigl( \omega \, (t-t_0) \bigr) \\ &= e + \frac{M}{m+M} \, A \: \cos\bigl( \omega \, (t-t_0) \bigr) \, . \end{align*} Hence, the weight is approximately at rest while the cart oscillates with a frequency \begin{align*} \omega = \sqrt{ k \: \frac{ m+M }{mM} } = \sqrt{ \frac{k}{M} \: (1+\varepsilon) } = \sqrt{ \frac{k}{M} } \; \left( 1 + \frac{\varepsilon}{2} - \frac{\varepsilon^2}{8} + \cdots \right) \, . \end{align*} This is the eigenfrequency of the system of a cart that is fixed to a support by the spring. The weight is much heavier than the cart, and due to its inertia it serves as a fixed support.
6.5.3 Self Test
Problem 6.14: Center-of-mass coordinates for many-body systems
Consider a system of $N$ particles with masses $m_i$ and position $\mathbf x_i(x)$, $i\in\{1,\cdots,N\}$,
and let the potential energy be a function of the particle distances $\mathbf R_{ij} = \mathbf x_i - \mathbf x_j$.
Show that:
a) The Lagrangian of the system can be expressed in terms of the the center of mass of the system,
\begin{align*}
\mathbf Q = \frac{\sum_{i=1}^N m_i\, \mathbf x_i}{\sum_{i=1}^N m_i}
\end{align*}
and the relative coordinates $\mathbf R_{1j}$, $j \in\{2,\dots,N\}$.
b) The center of mass is a cyclic variable, and the associated conserved quantity is the total momentum \begin{align*} \mathbf P = \sum_{i=1}^N m_i\, \dot{\mathbf x}_i \end{align*}
c) The other DOF can be described in terms of the particle distances $\{ \mathbf R_{i1}\, , \; 1<i\leq N \}$.
Hint:
d) What changes when gravity is acting on the particles.
e) What happens when there is a constant external force (i.e., the same force for all particles).
Problem 6.15: Pendulum on rails
We set a mathematical pendulum on a cart that can move without friction horizontally in the direction of motion of the pendulum.
The cart has an overall mass $M$.
This mass will also include the pendulum frame which is considered to be a part of the cart.
The pendulum comprises of a mass $m$ that moves on an arm of length $\ell$.
We choose the coordinates such that the fulcrum of the pendulum is located at $(x(t), 0)$,
and the mass of the pendulum at $(x+\ell\sin\theta, -\ell\cos\theta)$.
a) Sketch the setup, indicating the parameters and coordinates of the problem.
b) Determine the kinetic energy of the cart, the kinetic energy of the pendulum weight, and the potential energy of the pendulum weight. Provide the resulting Lagrange function for the pendulum on the cart.
c) Identify the equation of motion for $x$, and show that it leads to a conserved quantity of the form
\[
p_x = \alpha \; \dot x + \beta \; \dot\theta \; \cos\theta
\]
How do $\alpha$ and $\beta$ depend on the parameter $\ell$, $m$, $M$, and $g$?
d) Determine the $x$-component of the center of mass of the pendulum weight and the cart.
Which interpretation does this provide for the result of part ©?
e) In the following we work in the center of mass frame,
where $p_x = 0$.
Show that the equation of motion for $\theta$ will then take the form
\[
\ddot\theta = -\sin\theta \; \frac{1+ \mu\; \dot\theta^2 \: \cos\theta }{ 1 - \mu \, \cos^2\theta }
\]
This form of the equation involves a particular form of the dimensionless time scale!
Which time scale has been chosen?
How does $\mu$ depend on the masses $m$ and $M$?
* f) Why is it clear a priori that $\mu$ can only depend on $m$ and $M$ and not on the other parameters of the problem, $g$ and $\ell$?
* g) In the limit $\mu \to 0$ one recovers the equation of motion of the mathematical pendulum.
Why would one expect this result?

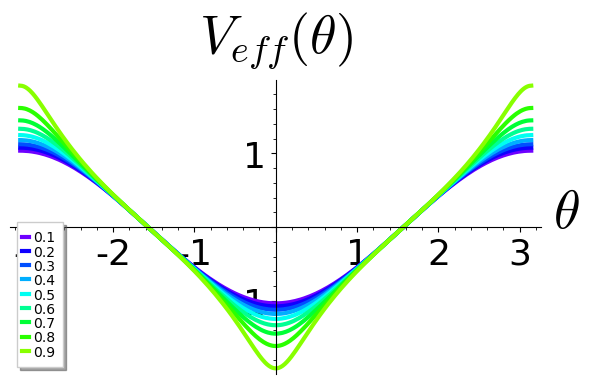
* i) The plot in the margin shows the effective potential for different values of $\mu$. For small $\mu$ it amounts to $V_{\text{eff}} \simeq \cos\theta$. For $\mu \to 1$ one obtains a very narrow, very deep potential. What does this tell about the motion of the pendulum in the two limiting cases? Underpin your conclusion for $\mu \to 1$ by showing that in this limit the dimensionless height $y$ of the pendulum weight obeys the EOM \begin{align*} \ddot{y} = -1 \end{align*} What will be its position $x$?