Table of Contents
4.6 Employing constants of motion - the center of mass (CM) inertial frame
One of the most important objectives of physics is the description of the motion of interacting particles. As a first step in this direction we discuss how to employ constants of motion to determine the motion of two point particles that interact with a conservative force depending only on the scalar distance between the particles, the interaction most commonly encountered in physical systems. The impact of spatial extension will be the topic of Chapter 5.
Definition 4.6 Point Particles
A point particle is an idealization of a physical object
where its mass is considered to be concentrated in a single point in space $\mathbf x$.
Point particles can not collide.
However, their motion can be subjected to forces that depend on their position $\mathbf x$.
Example 4.10 Kepler Problem
The Kepler problem addresses the motion of a planet of mass $m$
that orbits around a sun of mass $M$.
The sun and the planet are so far apart
that it is justified to consider their masses as concentrated
in the positions $\mathbf q_P$ and $\mathbf q_S$,
and to approximate their interaction as arising from the potential
\begin{align*}
\Phi( R ) = -\frac{ mMG }{ R }
\end{align*}
where $G = 6.67259 \times 10^{-11}\, \, m^3 kg^{-1} s^{-2}$ is the constant of gravitation and $R = \lvert \mathbf q_P - \mathbf q_S \rvert$ is the distance between planet and sun.
Planet and sun are considered as point particles.
Remark 4.12. The approximation of point particles has been introduced by Newton upon providing the first mathematical model for the Kepler problem. Subsequently, it has extremely successfully been applied in celestial mechanics. Celestial Mechanics addresses the problem of discussing the motion of all planets and their moons based on pair interactions deriving from the potential provided in Example 4.10. How to the tiny interactions between the planets impact their motion over long times? Is our solar system stable, or will–at some time in the far future–some planet or moon borrow energy from the other bodies and escape into outer space?
Remark 4.13. A straightforward application of the Kepler problem is the discussion of the motion of the Moon around Earth where the predictions have been tested extremely accurately based on satellite data and the return time of light signals send to Moon and reflected by mirrors on its surface that have been left there by space missions. The measurements clearly reveal the limitations of the model: Most noticeably, the Moon gives rise to tidal forces on Earth that induce a tiny amount of dissipation. Even in celestial mechanics there are small dissipative corrections to conservative interaction.
In Section 3.4 we learned that conservation laws impose constraints on the motion of bodies that can be used to simplify the description of their motion. We consider the motion of $N$ particles of masses $m_i$, $i=1,\dots,N$ at the positions $ \mathbf q_i$, $i=1, \dots , N $ that are subjected to forces $\mathbf F_{ij}$ acting between every pair $(i,j)$ of particles. There is not self-interaction $\mathbf F_{ii} = \mathbf 0$, and the forces obey Newtons 3rd law, $\mathbf F_{ij} = - \mathbf F_{ji}$. Moreover, they are conservative, and depend only on the distance of the particles, $\mathbf F_{ij} = \nabla \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert \bigl)$. Here the indices $ij$ indicate that the force may depend on additional scalar parameters such as the mass or charge of the particles.
4.6.1 Center of mass motion and relative motion
We first determine the evolution of the position of the center of mass $\mathbf Q$ of the system \begin{align} \mathbf Q = \frac{1}{M} \sum_i m_i \: \mathbf q_i \quad\text{with total mass}\quad M = \sum_i m_i \tag{4.6.1} \end{align} Its evolution is not subjected to external forces \begin{align} \ddot{\mathbf Q} = \frac{1}{M} \sum_i m_i \: \ddot{\mathbf q_i} = \frac{1}{M} \sum_i \sum_j \mathbf F_{ij} = \mathbf 0 \tag{4.6.2} \end{align} due to Newtons 3rd law. Hence, we find for an initial position $\mathbf Q_0$ and initial velocity $\mathbf V_0$ at an initial time $t_0$ that
\begin{align} \mathbf Q(t) = \mathbf Q_0 + \mathbf V_0 \: ( t - t_0 ) \tag{4.6.3} \end{align} Now we introduce the coordinates relative to the center of mass $\mathbf r_i = \mathbf q_i - \mathbf Q$ and we observe that \begin{align} m_i \, \ddot{\mathbf r}_i &= m_i \, \ddot{\mathbf q}_i - m_i \, \ddot{\mathbf Q} = m_i \, \ddot{\mathbf q}_i \nonumber \\ &= \sum_j \mathbf F_{ij} = - \nabla_{\mathbf q_i} \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert \bigr) = -\frac{ \mathbf q_i - \mathbf q_j }{ \lvert \mathbf q_i - \mathbf q_j \rvert } \; \Phi_{ij}'\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert \bigr) \nonumber \\ &= -\frac{ \mathbf r_i - \mathbf r_j }{ \lvert \mathbf r_i - \mathbf r_j \rvert } \; \Phi_{ij}'\bigl( \lvert \mathbf r_i - \mathbf r_j \rvert \bigr) \tag{4.6.4} \end{align} where $\Phi_{ij}'(x)$ denotes the derivative of $\Phi_{ij}(x)$ with respect to its scalar argument $x$. Hence, the EOMs for $\mathbf Q$ and for the positions $\mathbf r_i$ relative to the center of mass can be solved separately of each other, and the EOM for the CM has a trivial solution, Equation 4.6.3. We may therefore always address the motion of the particles in a setting where their center of mass is fixed at the origin of the coordinate system.
4.6.2 Angular momentum in celestial mechanics
The total angular momentum is conserved for systems where all forces are due to pairwise interactions between particles pairs of particles $ij$ that obey Newtons 3rd law $\mathbf F_{ij} = - \mathbf F_{ji}$ with forces acting along the line connecting particle $i$ and $j$, i.e., in particular for the forces of the form given in Equation 4.6.4. After all,
\begin{align*} \mathbf L &= \sum_i \mathbf q_i \times m_i \, \dot{\mathbf q}_i = \sum_i \bigl( \mathbf Q + \mathbf r_i \bigr) \times m_i \: \bigl( \dot{\mathbf Q} + \dot{\mathbf r}_i \bigr) \\ &= \sum_i \bigl( m_i \, \mathbf Q \times \mathbf Q + \mathbf Q \times m_i \,\dot{\mathbf r}_i + m_i \,\mathbf r_i \times \dot{\mathbf Q} + \mathbf r_i \times m_i \, \dot{\mathbf r}_i \bigr) \\ &= M \mathbf Q \times \dot{\mathbf Q} + \sum_i \mathbf r_i \times m_i \, \dot{\mathbf r}_i \end{align*} where the terms that contain only a single factor of $\mathbf r_i$ or $\dot{\mathbf r}_i$ vanish because $\sum_i m_i \, \mathbf r_i = \sum_i m_i \, \bigl( \mathbf q_i - \mathbf Q \bigr) = \mathbf Q - \mathbf Q = \mathbf 0$. Now we have \begin{align*} M \, \ddot{\mathbf Q} = \sum_i m_i \, \ddot{\mathbf q}_i = \sum_i \sum_j \mathbf F_{ij} = \sum_{i<j} \mathbf F_{ij} + \mathbf F_{ji} = \mathbf 0 \end{align*} such that we obtain for the time derivative \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathbf L &= M\, \mathbf Q \times \ddot{\mathbf Q} + \sum_i \mathbf r_i \times m_i \,\ddot{r}_i = \mathbf Q \times M\,\ddot{\mathbf Q} + \sum_i \mathbf r_i \times \sum_j \mathbf F_{ij} \\ &= \frac{1}{2} \: \left( \sum_{ij} \mathbf r_i \times \mathbf F_{ij} - \sum_{ij} \mathbf r_i \times \mathbf F_{ji} \right) \\ &= \frac{1}{2} \: \left( \sum_{ij} \mathbf r_i \times \mathbf F_{ij} - \sum_{ij} \mathbf r_j \times \mathbf F_{ij} \right) \\ &= \frac{1}{2} \: \sum_{ij} \bigl( \mathbf r_i - \mathbf r_j \bigr) \times \mathbf F_{ij} = \mathbf 0 \end{align*} Upon moving to the second line we used that $\ddot{\mathbf Q} = \mathbf 0$, and the antisymmetry of the forces $\mathbf F_{ij} = - \mathbf F_{ji}$. Moving to the third line we swapped the names of the summation indices $i$ and $j$. In the last line, we collected terms and used that $\mathbf F_{ij}$ is parallel to $\mathbf r_i - \mathbf r_j$. We summarize this important finding the following
Theorem 4.1 Angular momentum conservation
The relative angular momentum is conserved for systems with pairwise interaction forces acting parallel to the distance between particles.
The total angular momentum is conserved
when external forces vanish or
when they give rise to a center-of-mass forces
$M \ddot{\mathbf Q}$ aligned parallel to $\mathbf Q$.
Remark 4.14. An example for the latter case is a harmonic force $\mathbf F_i = c \, m_i \, \mathbf q_i$. The proof is provided as Problem 4.19 c).
Conservation of the relative angular momentum implies important constraints on the motion. In celestial mechanics this is vividly displayed in the shape of galaxies, solar systems and planetary ring structures. All these systems emerge by the gravitational collapse of large stellar dust clouds. Let cloud be spherically symmetric and uniform initially, consisting of a huge number of small dust particles. By statistical fluctuations the cloud will have an angular momentum, of the order of $M \, D^2 \, \omega$ where $M$ is the total mass of the cloud, $D$ is the diameter of the cloud and $\omega$ is a tiny number with the unit of a rotation frequency. For a solar system the cloud will collapse until virtually all of its mass is concentrated eventually in the sun in its very center. This involves a change of the diameter of the region holding the mass of about $10^4$. For conserved angular momentum the frequency $\omega$ is growing by a factor of $10^8$. In Problem 4.17 you will show that the initial angular momentum can not be coped by a spin of the central star. The competing constraints of the tendency of gravity to lump together the matter in the cloud and the need to conserve angular moment eventually form a solar system with a central very massive star or double star that is surrounded by planets moving around the star at a distance large as compare to the size of the star.
4.6.7 Self Test
Problem 4.16: The CM of the solar system and the position of the sun
Verify that the center of mass of Sun can lie more than a sun-diameter away from the center of mass of the solar system.
Problem 4.17: Angular momentum of the solar system
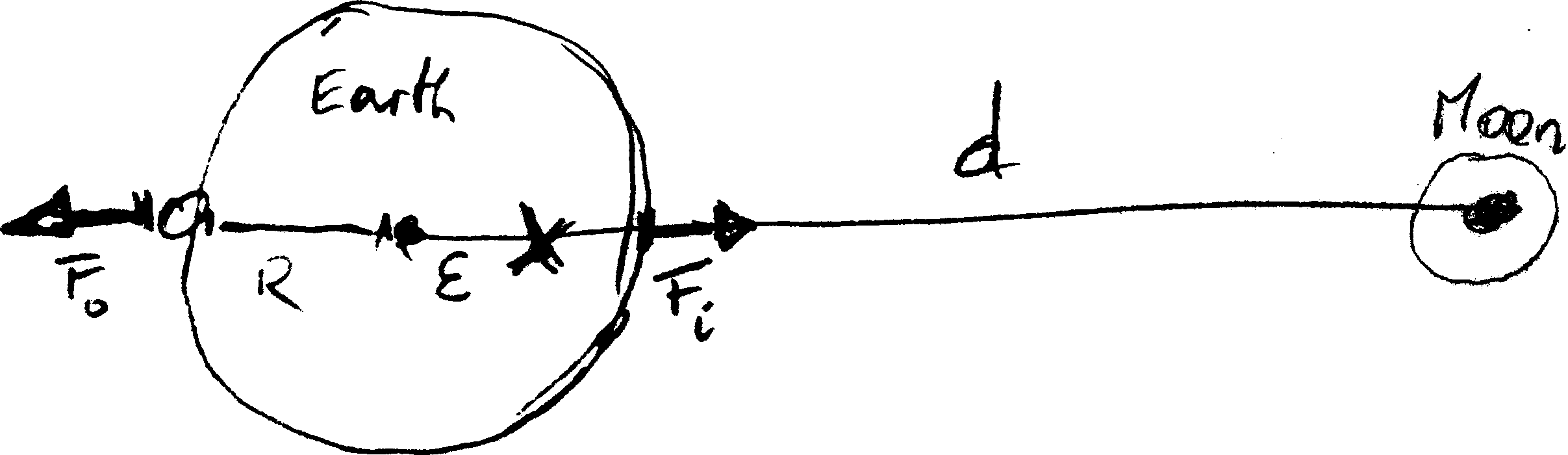 Figure 4.12: Distances adopted for the estimate of the forces inducing tidal forces $F_o$ and $F_i$:
The distance $d$ between Earth and Moon,
the Earth radius $R$, and
the distance $\epsilon$ between the center of mass of Earth and the joint center of mass of Earth and Moon (indicated by a cross $\times$).
Tides emerge at the side facing the Moon (inwards) and opposing the Moon (outwards).
Figure 4.12: Distances adopted for the estimate of the forces inducing tidal forces $F_o$ and $F_i$:
The distance $d$ between Earth and Moon,
the Earth radius $R$, and
the distance $\epsilon$ between the center of mass of Earth and the joint center of mass of Earth and Moon (indicated by a cross $\times$).
Tides emerge at the side facing the Moon (inwards) and opposing the Moon (outwards).
The solar system has a total angular momentum of about $L_{SoSy} = 3.3212 \times 10^{45}\, \, \text{kg m$^2$ s^{-1}}$.
- Assume that the mass was initially distributed in a ball of a radius of about 40 \, AU. Estimate the corresponding effective frequency $\omega$.
- Assume that the mass in concentrated in two point particles that circulate around each other at a distance of about the sun diameter. Compare their rotation speed to the speed of light.
- Verify that 98% of $L_{SoSy}$ is accounted for by the orbital angular momenta of the planets
- How does this imply the disk-like structure of our solar system?
- Speculate about other effects that contribute to the remaining 2% of the total angular momentum.
Problem 4.18: Tidal forces
Gravitational forces of Moon and centripetal forces due to the rotation with frequency
$\Omega = 1/$month of Earth around the common center of mass of Earth and Moon
(cross in Figure 4.12) give rise to tides.
On the outwards facing side the resulting acceleration on a mass element on the Earth surface
can be estimated as
\begin{align*}
a_0 = g - (\epsilon+R) \, \Omega^2 + \frac{G\,M_M}{(d+R)^2}
\end{align*}
where $M_M$ is the Moon mass.
a) Assume that Earth and Moon evolve on circular paths and employ the force balance for a stable motion in order to show that
\begin{align*}
a_0 = g
- R\, \Omega^2 \; \left[
1 - \frac{M_M}{M_E+M_M} \: \frac{R}{d} \; \left( 1 + \mathcal O( R/d) \right)
\right]
\end{align*}
and determine the higher-order correction terms that are indicated here as $\left( 1 + \mathcal O( R/d) \right)$.
b) Determine also the change of the acceleration on the side towards the moon. How does it differ from $a_i$?
c) Determine the relative change of the gravitational acceleration due to the presence of moon,
and the difference between $a_i$ and $a_o$.
b) So far we only discussed the component of the acceleration along a line connecting Earth and Moon at the innermost and outermost points of the Earth surface.
What about the other components of the gravitational acceleration: when considering tides at mid latitudes? at positions half-way between the two points (i.e., top and bottom sides of Earth in the figure).
c) What is the impact of the Earth rotation?
How does it break the symmetry?
What does this imply about the relative strength of the two tidal waves every day?
Problem 4.19: Center of mass and constants of motion
How do the expressions for the constants of motion discussed in Section 3.4
behave when separating the center of mass motion and the relative motion,
$\mathbf q_i(t) = \mathbf Q(t) + \mathbf r_i(t)$.
a) Show that the kinetic energy $T = \sum_i m_i \dot{\mathbf q}_i^2$ takes the new value \begin{align*} T = \frac{M}{2} \; \dot{\mathbf Q}^2 + \sum_i \frac{m_i}{2} \: \dot{\mathbf r}_i^2 \end{align*}
b) Assume that the system is moving in a gravitational field, and that the other forces on the particle arise from pair-wise conservative interactions as discussed Equation 4.6.4. Show that the total energy can be written as \begin{align*} E = \frac{M}{2} \; \dot{\mathbf Q}^2 - M \mathbf g \cdot \mathbf Q + \sum_i \frac{m_i}{2} \: \dot{\mathbf r}_i^2 + \sum_{i<j} \Phi_{ij}\bigl( \lvert \mathbf r_i - \mathbf r_j \rvert \bigr) \end{align*}
c) Show that the total angular momentum is conserved for a systems with the particles interactions given in Equation 4.6.4 and an additional external force \begin{align*} \mathbf F_i = c \, m_i \, \mathbf q_i \\ \end{align*} acting on each particle $i$.
