Table of Contents
5.3 Volume integrals — A professor falling through Earth
The center of mass of a set of particles was defined in Equation 4.6.1 as a weighted sum of their positions. Now we consider an extended object that is characterized by a mass distribution $\rho(\mathbf q)$. We will always assume that the distribution varies slowly in space in side the object. Outside it vanishes. The weighted sum over the particle positions will then be generalized to become a volume integral.
5.3.1 Determine volume and mass by volume integrals
In Section 3.4.2 we introduced line integrals by dividing the integration path into small steps $\{ s_i \}$, and approximating the integral as a sum over the contributions of the individual pieces. The definition of a volume integrals proceeds analogously. Now, we integrate over a region $R \subset \mathbb R^D$, and we start by partitioning this region into small volume elements $\Delta V_i$.
Definition 5.1 Partition of Space
A set $\{ \Delta V_i\, , \;\; i \in \mathsf{I} \}$ is a partition of a region $R \subset \mathbb R^D$
iff
- $\displaystyle \forall i \in \mathsf{I} \; : \; \Delta V_i \subset R $,
- $\displaystyle \forall i,j \in \mathsf{I} \; : \; i \neq j \Rightarrow \Delta V_i \bigcap \Delta V_j = \emptyset $,
- $\displaystyle \forall x \in R \; \exists i \in \mathsf{I} \; : \; x \in \Delta V_i $.
Definition 5.1 entails that the union of the elements of the partition amounts to the region $R$, \begin{align*} R = \bigcup_{i \in \mathsf{I}} \Delta V_i \end{align*} Let now $V = \| R \|$ denote the volume of the region $R$. For every partition it can be written as \begin{align*} V = \| R \| = \sum_{i \in \mathsf{I}} \| \Delta V_i \| \end{align*} In the limit of small volume elements we write this sum as a
Definition 5.2 Volume Integral
The volume integral $F$ of a function $f(\mathbf q)$ over a region $R \subset \mathbb R^D$ is defined as follows as limit of a sum over the elements of a partition,1) $\{ \Delta V_i\, , \;\; i \in \mathsf{I} \}$ of $R$ and points $\mathbf q_i \in \Delta V_i$,
\begin{align*}
F
= \int_R \mathrm{d}^D q \; f( \mathbf q )
= \lim_{ \| \Delta V_i \| \to 0 } \sum_{ i \in \mathsf i } \| \Delta V_i \| \, f( \mathbf q_i )
\end{align*}
For Cartesian coordinates $(q_1, q_2, \dots, q_D)$ the integration volume element is
$\mathrm{d}^D q = \mathrm{d} q_1 \cdots \mathrm{d} q_D$ and the integral amounts to
\begin{align*}
F = \int_{I_1} \mathrm{d} q_1 \: \int_{I_2(q_1)} \mathrm{d} q_2 \cdots \int_{I(q_1, \cdots, q_{D-1}} \mathrm{d} q_D \; f( q_1, \cdots, q_D )
\end{align*}
where the boundaries of the integrals must be chosen such that $( q_1, \cdots , q_D) \in R$.
Remark 5.2. For the function $f( \mathbf q ) = 1$ the volume integral provides the $D$-dimensional volume of the region $R$.
The mass $m(V)$ contained in a volume $\mathcal V$ can be expressed as a volume integral \begin{align*} m(V) &= \int_{\mathcal V} \mathrm{d}^3 q \: \rho( \mathbf q ) = \int_{\mathcal V} \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z \: \rho( x, y, z ) \\ &= \int_{x_{\text{min}}}^{x_{\text{max}}} \mathrm{d} x \; \left[ \int_{y_{\text{min}}(x)}^{y_{\text{max}}(x)} \mathrm{d} y \; \left( \int_{z_{\text{min}}(x,y)}^{z_{\text{max}}(x,y)} \mathrm{d} z \: \rho( x,y,z ) \right) \right] \end{align*} where the integration runs over all $\mathbf q \in \mathcal V$, a volume with smallest $x$-value $x_{\text{min}}$ and largest $x$-value $x_{\text{max}}$, its $y$-values between $y_{\text{min}}(x)$ and $y_{\text{max}}(x)$ for a given $x$, and $z$-values between $z_{\text{min}}(x,y)$ and $y_{\text{max}}(x,y)$ for given $x$ and $y$.
Remark 5.3. We adopt the convention that the mass density is zero outside an object. As a consequence its total $M$ mass is obtained as \begin{align*} M = \int_{\mathbb R^3} \mathrm{d}^3 q \: \rho( \mathbf q ) \end{align*} The boundaries of the integral that define the shape of the body have been absorbed into the definition of the density.
We illustrate the steps taken to evaluate a volume integral by calculating the area and volume of some simple geometric shapes:
Example 5.1 Surface areas of rectangles and circles
a) The surface area of the rectangle $R \subset \mathbb R^2$ with $(x,y) \in R$ iff $0 \leq x \leq a$ and $-b < y < b$ is \begin{align*} \| R \| = \int_R \mathrm{d}^2 q = \int_0^a \mathrm{d} x \: \int_{-b}^b \mathrm{d} y = 2ab \end{align*}
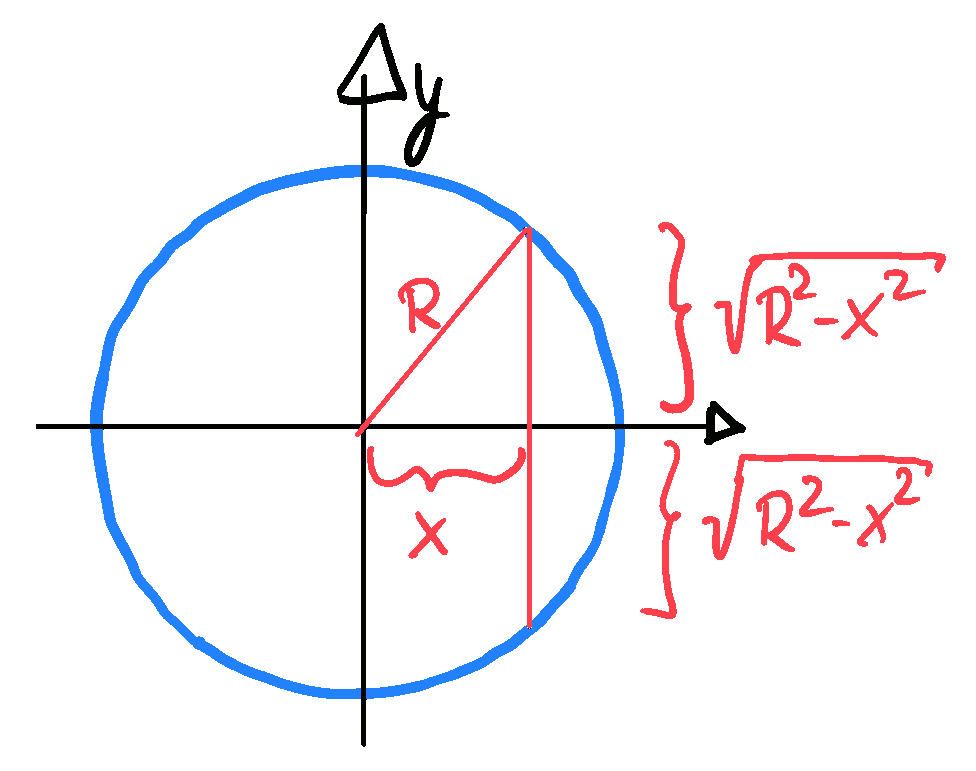
b) The surface area of the circle $C$ with center at the origin and radius $R$ is \begin{align*} \| C \| &= \int_C \mathrm{d}^2 q = \int_{-R}^R \mathrm{d} x \: \int_{-\sqrt{R^2-x^2}}^{\sqrt{R^2-x^2}} \mathrm{d} y = 2\: \int_{-R}^R \mathrm{d} x \: \sqrt{R^2-x^2} \\ &= 2\, R^2 \, \int_{-\pi/2}^{\pi/2} \mathrm{d}\theta \: \cos\theta \; \sqrt{1-\sin^2\theta} = 2\, R^2 \, \int_{-\pi/2}^{\pi/2} \mathrm{d}\theta \: \cos^2\theta \\ &= R^2 \, \int_{-\pi/2}^{\pi/2} \mathrm{d}\theta \: \bigl( \cos^2\theta + \sin^2\theta \bigr) = \pi \, R^2 \end{align*}
The choice of the integration boundaries is illustrated in Figure 5.8. Upon moving to the second line of this equation we substituted $x=R \, \sin\theta$, and in the step to the third line we made use of the $\pi$-periodicity of $\cos^2\theta$.
Figure 5.8: Notations adopted in the surface integral performed in Example 5.1 b.
Example 5.2 Volume of a sphere
The volume of a three-dimensional sphere $S$ with center at the origin and radius $R$ is
\begin{align*}
\| S \|
&= \int_S \mathrm{d}^2 q
= \int_{-R}^R \mathrm{d} x \: \int_{-\sqrt{R^2-x^2}}^{\sqrt{R^2-x^2}} \mathrm{d} y \: \int_{-\sqrt{R^2-x^2-y^2}}^{\sqrt{R^2-x^2-y^2}} \mathrm{d} z
\\
&= \int_{-R}^R \mathrm{d} x \: \pi \, \left( \sqrt{R^2 - x^2} \right)^2
= \pi \int_{-R}^R \mathrm{d} x \: \left( R^2 - x^2 \right)
\\
&= \pi \, \left( 2 \, R^3 - \frac{2}{3} \, R^3 \right)
= \frac{4\, \pi}{3} R^3
\end{align*}
Upon moving to the second line we observed that the $y$ and $z$ integrals agreed with the ones performed
to evaluate the are of a circle, cf Example 5.1 b.
5.3.2 Change of variables
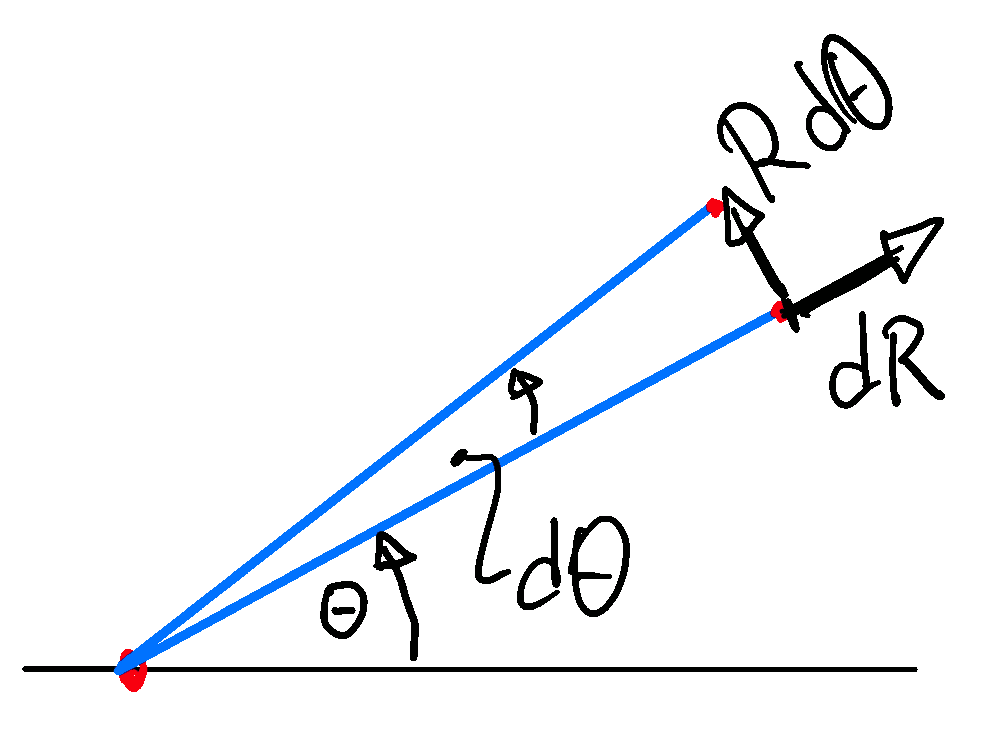
The shape of a circle with center at the origin and radius $R$ can much easier be described by polar coordinates rather than Cartesian coordinates2): $\{ (\rho, \theta) \in \mathbb R^+ \times [0,2\pi) \; : \; \rho < R \}$. To take advantage of this simplification we have to introduce a transformation of the integration coordinates from Cartesian to polar coordinates. A heuristic guess based on Figure 5.9 suggests that a volume element $\mathrm{d} x\, \mathrm{d} y$ at the position $(x,y)=(\rho\,\cos\theta, \rho\,\sin\theta)$ should be replaced by $\rho \, \mathrm{d}\theta\, \mathrm{d} \rho$. One readily verifies that this is a reasonable choice by working out the area of the circle with radius $R$:
\begin{align*} \| C \| = \int_C \mathrm{d}^2 q = \int_0^R \mathrm{d} R \: \int_0^{2\pi} \mathrm{d}\theta\, R = \pi \, \int_0^R \mathrm{d} R \: 2\,R = \pi \, R^2 \end{align*} with a much easier calculation than in Example 5.1 b. Formally the change of the integration volume is determined by generalizing the substitution rule for integrals, as illustrated in Figure 3.13 for one dimensional integrals. In this rule the derivative $f'(x)$ account for the change of the width of the rectangles that are summed to approximate the integral. In order to generalize this idea we recall from the discussion of line integrals that \begin{align*} \frac{\mathrm{d} \mathbf q}{\mathrm{d} R} \: \mathrm{d} R = \begin{pmatrix} \cos\theta \\ \sin\theta \end{pmatrix} \: \mathrm{d} R \quad\text{ and }\quad \frac{\mathrm{d} \mathbf q}{\mathrm{d} \theta} \: \mathrm{d} \theta = \begin{pmatrix} -R\, \sin\theta \\ R \, \cos\theta \end{pmatrix} \: \mathrm{d} R \end{align*} In general the derivatives involved in the definition of the length elements do not have unit length and they need not be orthogonal. Their length reflects the change of the length unit that we also encounter in the one-dimensional case. The angle between the vectors indicates that in two-dimensions one can also partition space by using parallelograms rather than rectangle. The unit area for the integration will always be the area spanned by the two vectors. In $D$ dimensions the integration volume is defined by the volume spanned by the $D$ derivative vectors of the position vector $\mathbf q$ with respect to the new coordinates. It is commonly expressed in terms of the Jacobi determinant. We first introduce the notion of a
Definition 5.3 Determinant
The determinant of a matrix amounts to the volume spanned by its column vectors.
For a matrix $\mathsf A$ it is denoted as $\det\mathsf A$.
Remark 5.4. The determinant of $2\times 2$ and $3\times 3$ matrices takes the form of the (sum of) products along the diagonals from left to right minus the (sum of) products of the diagonals from right to left, \begin{align*} \det\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} &= a_{11} \, a_{22} - a_{12} \, a_{21} \\ \det\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} &= a_{11} \, a_{22} \, a_{33} + a_{12} \, a_{23} \, a_{31} + a_{13} \, a_{21} \, a_{32} \\ &\; -a_{11} \, a_{23} \, a_{32} + a_{22} \, a_{31} \, a_{13} + a_{33} \, a_{12} \, a_{21} \end{align*} These expressions are entailed by the geometric interpretation of the cross product in Section 2.9.2.
Without proof we provide the following general rule for calculating determinants
Theorem 5.1 Recursive calculation of determinants
Let $\mathsf A$ be a $D\times D$ matrix with $D \in \mathbb N$
and entries $a_{ij}$ where $i,j \in \{ 1, \cdots, D \}$.
For $D = 1$ we define $\det \mathsf A = a_{11}$.
For $D > 1$ we introduce the $(D-1)\times (D-1)$ submatrices $\mathsf A_{ij}$
that are obtained from $\mathsf A$ by dropping its $i$th row and $j$th column.
The determinant of $\mathsf A$ can then be calculated by a recursion
that either works along a row $j$ or a column $k$ of $\mathsf A$,
\begin{align*}
\det\mathsf A
= \sum_{j=1}^{D} (-1)^{j+k} \: \det\mathsf A_{jk}
= \sum_{k=1}^{D} (-1)^{j+k} \: \det\mathsf A_{jk}
\end{align*}
Altogether this allows us to identify the factor involved in a change of the integration variables as the Jacobi determinant.
Theorem 5.2 Jacobi matrix and determinant
We consider a change of integration variables from the coordinates
$\mathbf x = (x_1, x_2, \cdots, x_D)$ to $( y_1, y_2, \cdots , y_D)$
that is defined by the functions
$x_1(\mathbf y)$, $x_2(\mathbf y)$, $\cdots$, $x_D(\mathbf y)$.
Then the integration volume changes as
\begin{align*}
\mathrm{d} x_1 \cdots \mathrm{d} x_D
= \det\begin{pmatrix}
\frac{ \partial x_1 }{ \partial y_1 } & \frac{ \partial x_1 }{ \partial y_2 } & \dots & \frac{ \partial x_1 }{ \partial y_D } \\
\frac{ \partial x_2 }{ \partial y_1 } & \frac{ \partial x_2 }{ \partial y_2 } & \dots & \frac{ \partial x_2 }{ \partial y_D } \\
\vdots & \vdots & \ddots & \vdots \\
\frac{ \partial x_D }{ \partial y_1 } & \frac{ \partial x_D }{ \partial y_2 } & \dots & \frac{ \partial x_D }{ \partial y_D }
\end{pmatrix}
\mathrm{d} y_1 \cdots \mathrm{d} y_D
\end{align*}
The matrix involved in this transition is called the Jacobi matrix of the transition,
and the determinant is called the Jacobi determinant.
Example 5.3 Integration volumes
a) polar coordinates
$(x,y) = \rho \: (\cos\theta, \: \sin\theta)$
transform as
\begin{align*}
\mathrm{d} x \, \mathrm{d} y
= \det\begin{pmatrix}
\cos\theta & -\rho \sin\theta \\
\sin\theta & \rho \cos\theta
\end{pmatrix} \: \mathrm{d}\rho \, \mathrm{d} \theta
= \rho \, \mathrm{d}\rho \, \mathrm{d} \theta
\end{align*}
b) cylindrical coordinates
$(x,y,z) = (\rho \cos\theta, \: \rho \sin\theta, z)$
transform as
\begin{align*}
\mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z
= \det\begin{pmatrix}
\cos\theta & -\rho \sin\theta & 0\\
\sin\theta & \rho \cos\theta & 0 \\
0 & 0 & 1
\end{pmatrix} \: \mathrm{d}\rho \, \mathrm{d} \theta \, \mathrm{d} z
= \rho \, \mathrm{d}\rho \, \mathrm{d} \theta \, \mathrm{d} z
\end{align*}
c) spherical coordinates
$(x,y,z) = \rho \: (\sin\theta \cos\phi, \, \sin\theta \sin\phi, \, \cos\theta)$}
transform as
\begin{align*}
\mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z
= \rho^2 \, \sin\theta \, \mathrm{d}\rho \, \mathrm{d}\theta \, \mathrm{d}\phi
= \rho^2 \, \mathrm{d}\rho \, \mathrm{d}\!\cos\theta \, \mathrm{d}\phi
\end{align*}
5.3.3 The force of an extended object (Earth) on a point particle (professor)
As a first step towards discussing extended objects we consider the force exerted by an extended object on a point particle. The force is obtained by integrating the forces originating from the mass elements of the body, \begin{align*} \mathbf F_{\text{tot}} = \int_{\mathbb R^3} \mathrm{d}^3 q \: \mathbf F( \mathbf q ) \end{align*} where $\mathbf q$ is the vector from the position of the point particle to the mass element that is exerting the force. This expression involves the vector-valued generalization of volume integrals. It should be interpreted component-wise, stating the that the components $\mathbf F_{\text{tot}, i} = \hat{\boldsymbol e}_i \cdot \mathbf F_{\text{tot}}$ of the total force in some orthonormal base $\hat{\boldsymbol e}_x, \hat{\boldsymbol e}_y, \hat{\boldsymbol e}_z$ amount to \begin{align*} \hat{\boldsymbol e}_i \cdot \mathbf F_{\text{tot}} &= \int_{\mathbb R^3} \mathrm{d}^3 q \: \bigl( \hat{\boldsymbol e}_i \cdot \mathbf F( \mathbf q ) \bigr) \\ \text{or explicitly }\qquad \mathbf F_{\text{tot},x} &= \int_{\mathbb R^3} \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z \: F_x( x,y,z ) \\ \mathbf F_{\text{tot},y} &= \int_{\mathbb R^3} \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z \: F_y( x,y,z ) \\ \mathbf F_{\text{tot},z} &= \int_{\mathbb R^3} \mathrm{d} x \, \mathrm{d} y \, \mathrm{d} z \: F_z( x,y,z ) \\ \end{align*} The consequences can nicely be explored when an evil witch switches off electromagnetic interactions between a physics professor and its environment. In the absence of interaction with other matter the professor will freely fall towards the center of Earth, accelerated by a force that arises as sum of the mass elements constituting Earth (see Figure 5.10). For the professor of mass $m$ at position $\mathbf q_P$ and the mass element at position $\mathbf q_e$ this force amounts to $\mathbf F(\mathbf q_P, \mathbf q_e) = -\nabla ( m \, \rho(\mathbf q_e) \, G ) / \left\lvert \mathbf q_P - \mathbf q_e \right\rvert$. For simplicity we assume that Earth is spherical and that its mass density takes a uniform value $\rho = 3 \, M_E/ 4\pi \, R^3$. Then, the force on the professor takes the form
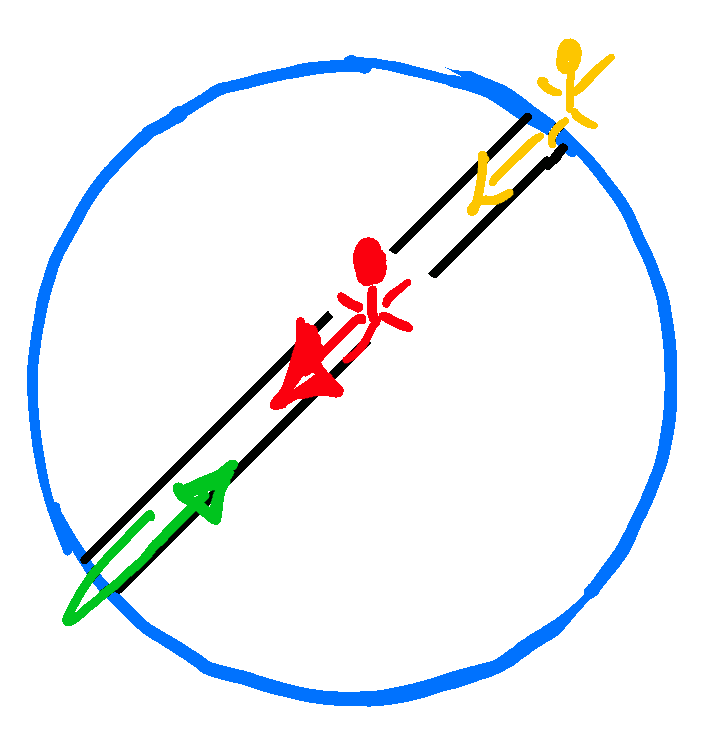 Figure 5.10: Initially positioned at the upper right (yellow), the professor will fall down (red),
and eventually pop out at the other side and return (green).
Figure 5.10: Initially positioned at the upper right (yellow), the professor will fall down (red),
and eventually pop out at the other side and return (green).
\begin{align} \mathbf F_{\text{tot}} &= - \int_{\mathbb R^3} \mathrm{d}^3 q \: \nabla \frac{ m \, \rho(\mathbf q_e) \, G }{ \left\lvert \mathbf q_P - \mathbf q_e \right\rvert } \tag{5.3.1} \\ &= - m \, \rho \, G \; \nabla \int_{\text{Earth}} \mathrm{d}^3 q \; \frac{1}{ \sqrt{ q_P^2 + q_e^2 - 2\, q_P \, q_e \, \cos\theta } } \tag{5.3.2} \end{align} where $\theta$ is the angle between the two vectors $\left\lvert \mathbf q_P \right\rvert$ and $\left\lvert \mathbf q_e \right\rvert$, while $q_P$ and $q_e$ denote their respective length. The integral is best evaluated by adopting a spherical coordinates $(r,\theta,\phi)$ for the integration where $r$ runs from zero to the Earth radius $R$, the angle $\theta$ from zero to $\pi$, and $\phi$ all around from zero to $2\pi$, \begin{align*} \mathbf F_{\text{tot}} &= - m \, \rho \, G \; \nabla \int_0^R \mathrm{d} r \: r^2\; \int_{-1}{1} \mathrm{d}\cos\theta \; \int_0^{2\pi} \mathrm{d}\phi \; \frac{1}{ \sqrt{ q_P^2 + r^2 - 2\, q_P \, r \, \cos\theta } } \\ &= - 2\pi\: m \, \rho \, G \; \nabla \int_0^R \mathrm{d} r \: r^2\; \left[ \frac{-1}{q_P\, r} \; \sqrt{ q_P^2 + r^2 - 2\, q_P \, r \, \cos\theta } \right]_{\cos\theta=-1}^{\cos\theta=1} \\ &= - 2\pi\: m \, \rho \, G \; \nabla \int_0^R \mathrm{d} r \: \frac{r}{ q_P }\; \Bigl( \left\lvert q_P + r \right\vert - \left\lvert q_P - r \right\rvert \Bigr) \\ &= - 4\pi\: m \, \rho \, G \; \nabla \left[ \frac{1}{q_P} \; \int_0^{q_P} \mathrm{d} r \; r^2 + \int_{q_P}^R \mathrm{d} r \; r \right] \\ &= m \, \rho \, G \; \nabla \left[ 2\pi R^2 - \frac{2\pi}{3} \mathbf q_P \cdot \mathbf q_P \right] = -\frac{m \, g}{R} \, \mathbf q_P \end{align*} In the last step we used that the acceleration on the Earth surface is $g = MG/R = 4\pi\,\rho\,R^2\,G/3$. The professor moves under the influence of a harmonic central force, as studied in Problem 4.19, Problem 4.21 and Problem 4.30!
After a while (cf Problem 5.12) he reappears at the very same spot where he started, except that Earth moved on while he was under way.
5.3.4 Self Test
Problem 5.5: Area of a parallelogram
Determine the area of the parallelogram defined by the points $(0,0), (1,3), (4,4), (2,1)$ by
- performing the volume integral,
- determining the area spanned by the two vectors that define the sides starting at the corner $(0,0)$.
—-
Problem 5.6: Volume of a solid of revolution
A solid of revolution is obtained by rotating some function $f(x)$
around the $x$ axis.
For instance, the function $\sqrt{R^2 - x^2}$ with $-R\leq x \leq R$
describes a sphere of radius $R$.
The volume $V$ of a solid of revolution are given by the integral
\begin{align} V = \pi \; \int \mathrm{d} x \: \left( f(x) \right)^2 \tag{5.3.3} \end{align}
- Sketch the function $f(x) = \sqrt{R^2 - x^2}$ and verify that the solid of revolution is indeed a sphere.
- Determine the volume of the sphere based on the given equation Compare you calculation and the result to the calculation given in Example 5.2.
- Show that the volume integral for a solid of revolution provides Equation 5.3.3 when one adopts cylindrical coordinates.
—-
Problem 5.7: Volume of a cone
Determine the volume of a cone with symmetry axis along the $z$-axis,
that stands on the $(x,y)$-plane where it traces a circle of radius $R$,
while its vertex is at $(0,0,H)$.
- Perform the volume integral with Cartesian coordinates.
- Perform the volume integral with cylindrical coordinates.
—-
Problem 5.8: Coordinate transformation to cylindrical coordinates
Determine the Jacobi matrix and its determinant for the transformation
from Cartesian to spherical coordinates, cf Example 5.3 c).