Table of Contents
3.6 Problems
3.6.1 Practicing Concepts
Problem 3.13:
Car on an air-cushion
We consider a car of mass $m=20 \, \text{g}$ moving – to a very good approximation without friction – on an air-cushion track.
There is a string attached to the car that moves over a roll and hangs vertically down on the side opposite to the car.
a) Sketch the setup and the relevant parameters.
b) Which acceleration is acting on the car when the string is vertically pulled down with a force of $F = 2 \, \text{N}$. Determine the velocity $v(t)$ and its position $x(t)$.
c) Determine the force acting on a $200 \, \text{g}$ chocolate bar, in order to get a feeling for the size of the force that was considered in b).
d) Now we fix the chocolate bar at the other side of the string. The velocity of the car can then be obtained based on energy conservation
\begin{align*}E = E_{\mathrm{kin}} + E_{\mathrm{pot}} = \frac{m+M}{2} \; v^2 + Mgh = \hbox{const}\end{align*}
where $M$ is the mass of the chocolate bar. Is the acceleration the same of different as in the cases b) and c)? Provide an argument for your conclusion.
Problem 3.14: 'Oumuamua
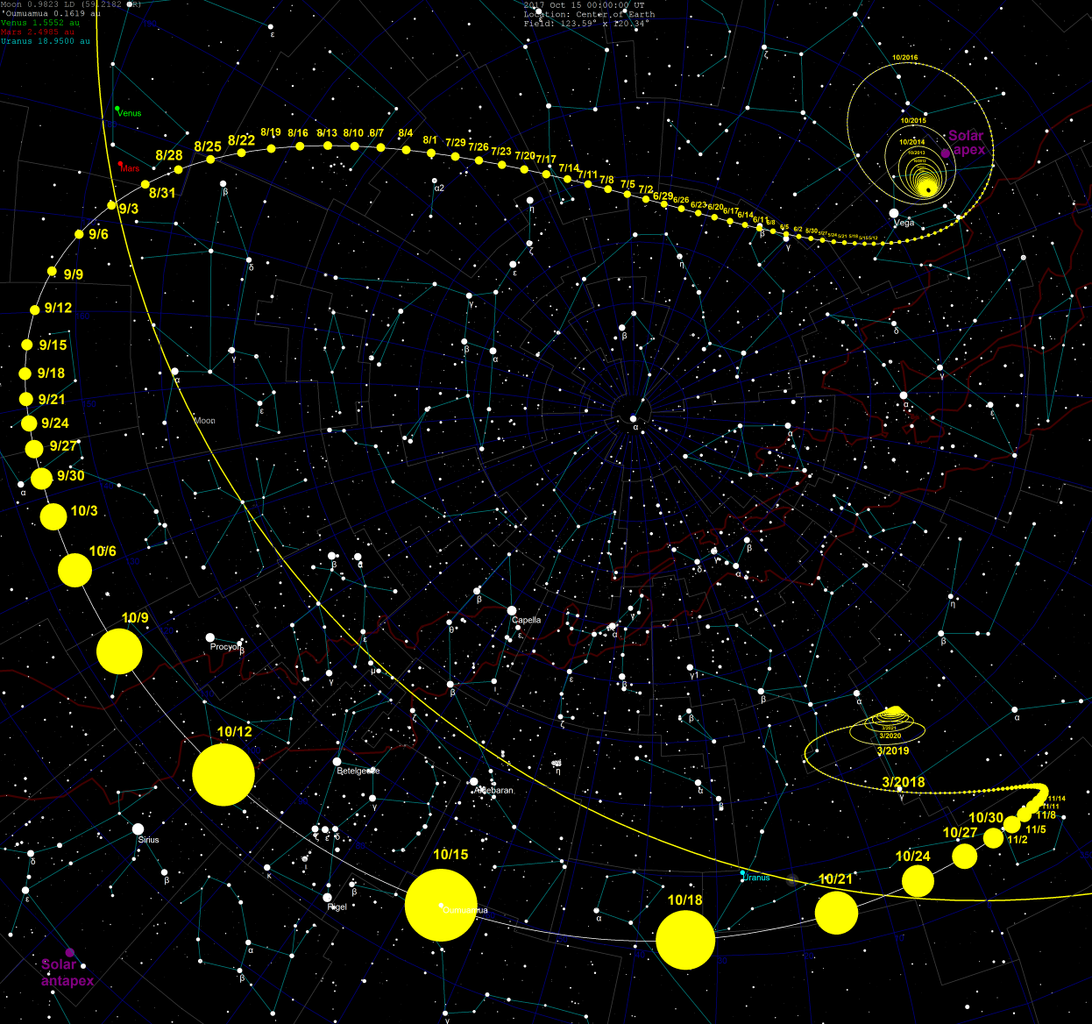 Tomruen/wikimedia, CC BY-SA 4.0
Tomruen/wikimedia, CC BY-SA 4.0
Figure 3.12: 'Oumuamua trajectory as seen by an observer on Earth.
On 19 October 2017 astronomers at the Haleakala Observatory in Hawaii discovered 'Oumuamua, the first interstellar object observed in our solar system. It approached the solar system with a speed of about $v_I = 26 \, \text{km/s}$ and reached a maximum speed of $v_P=87.71 \, \text{km/s}$ at its perihelion, i.e., upon closest approach to the sun on 9 September 2017.
a) Show that at the perihelion the speed and 'Oumuamua's smallest distance to the sun, $D$, obey the relation
\begin{align*}
\frac{v_P^2 - v_I^2}{2} = \frac{ M_S \, G }{ D }
\end{align*}
while for the Earth we always have
\begin{align*}
\frac{ 4 \pi^2 R }{T^2} \simeq \frac{ M_S \, G }{ R^2 }
\end{align*}
Here, $M_S$ is the mass of Sun,
$R$ is the Earth-Sun distance, and
$T=1 \, \text{year}$ is the period of Earth around Sun.
b) Show that this entails that
$\displaystyle
\frac{D}{R} = \frac{ 2 \, v_E^2 }{ v_P^2 - v_I^2 }
$,
where $v_E = 2\pi R/T$ is the speed of Earth around sun.
c) Use the relation obtained in b) to determine $D$ in astronomical units, and compare your estimate with the observed value $D = 0.25534(7) \, \text{AU}$.
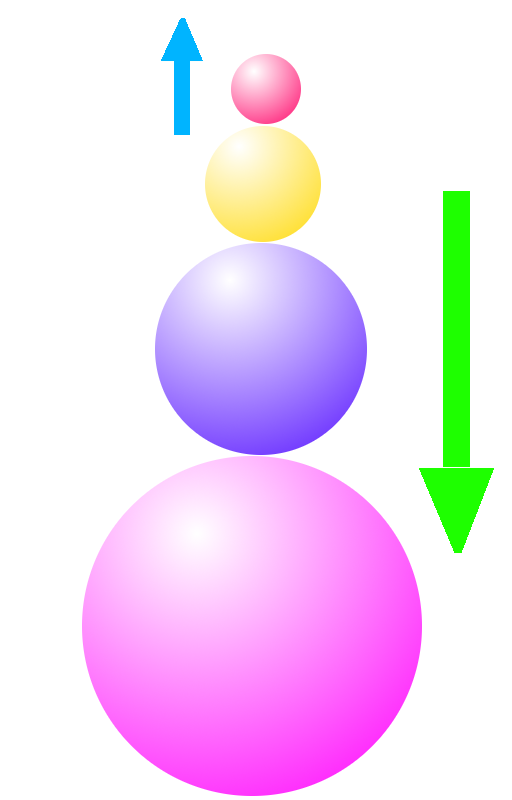
Problem 3.15:
Galilean cannon
In the margin we show a sketch of a Galilean cannon. Assume that the mass mass ratio of neighboring balls with always two, and that they perform elastic collisions.
- Initially they are stacked exactly vertically such that their distance is negligible. Let the distance between the ground the lowermost ball be $1 \, \text{m}$. How will the distance of the balls evolve prior to the collision of the lowermost ball with the ground?
- After the collision with the ground the balls will move up again. Determine the maximum height that is reached by each of the balls.
Problem 3.16:
Motion in a harmonic central force field
A particle of mass $m$ and at position $\mathbf r(t)$ is moving under the influence of a central force field
\begin{align*}
\mathbf F( \mathbf r ) = - k \, \mathbf r \, .
\end{align*}
- We want to use the force to build a particle trap,1) i.e., to make sure that the particle trajectories $\mathbf r(t)$ are bounded: For all initial conditions there is a bound $B$ such that $| \mathbf r(t) | < B$ for all times $t$. What is the requirement on the sign of the constant $k$ to achieve this aim?
- Determine the energy of the particle and show that its energy is conserved.
- Demonstrate that the angular momentum $\mathbf L = \mathbf r \times m\,\dot{\mathbf r}$ of the particle is conserved, too. Is this also true when considering a different origin of the coordinate system?
Hint:
Problem 3.17:
Collision with an elastic bumper
Consider two balls of radius $R$ with masses $m_1$ and $m_2$ that are moving along a line.
Their positions will be denoted as $x_1$ and $x_2$
in such a way that they touch when $x_1=x_2$ and they do not feel each other when $x_1 < x_2$.
When they run into each other, the balls can slightly be deformed
such that the distance between their centers takes the value $2R - d$,
and they experience a harmonic repulsive forces $\pm k \, d$.
We will say then that $d = x_2 - x_1 < 0$.
a) Newton's equations for the collision of the two balls take the form
\begin{align*}
m_1 \, \ddot x_1(t) &= -k \, d(t) &
m_2 \, \ddot x_2(t) &= k \, d(t)
\end{align*}
Show that this implies
\begin{align*}
\ddot d = - \omega^2 \, d
\end{align*}
for some positive constant $\omega$. How does $\omega$ depend on the spring constant $k$ and on the masses $m_1$ and $m_2$?
b) Let $d(t) = - d_M \: \sin\bigl( \omega \, (t-t_0) \bigr)$ describe the deformation of the balls for a collision at $t=t_0$, and contact in the time interval $t_0 \leq t \leq t_R$. Verify that it is a solution of the equation of motion.
At which time $t_R$ will the particles release (i.e. there is no overlap any longer)? What is the maximum potential energy stored in the harmonic potential?
c) We consider initial conditions where particle $1$ arrives with a constant velocity $v_0$ from the left,
and particle $2$ is at rest. What is the total kinetic energy in this situation?
Assume that at most a fraction $\alpha$ of the kinetic energy is transferred to potential energy.
What is the relation between $v_0$ and the maximum deformation $d_M$?
d) The velocity of the two particles at times $t_0 \leq t \leq t_R$
can now be obtained by solving the integrals
\begin{align*}
m_i \, \dot x_i(t) &= m_i \, x_i(t_0)
+ (-1)^i \; \int_{t_0}^t \mathrm{d} t' \: k \, d(t') \, ,
\quad\text{with } i \in \{1,2\}
\end{align*}
Why does this hold?
Which values does $x_i(t_0)$ take?
Solve the integral and show that
\begin{align*}
\dot x_1 &= v_0 \; \left[ 1 + \sqrt{\alpha\beta} \:
\Bigl( \cos( \omega \, (t-t_0) \bigr) - 1 \Bigr) \right]
\\
\dot x_2 &= v_0 \: \frac{m_1}{m_2} \; \sqrt{\alpha\beta} \:
\Bigl( \cos( \omega \, (t-t_0) \bigr) - 1 \Bigr)
\end{align*}
How does $\beta$ depend on the masses?
e) Verify that at release we have
\begin{align*}
\dot x_1 &= v_0 \; \bigl( 1 - 2 \, \sqrt{\alpha\beta} \bigr)
\\
\dot x_2 &= v_0 \; \frac{2\,m_1}{m_2} \, \sqrt{\alpha\beta} \bigr)
\end{align*}
Verify that these expressions comply to momentum conservation.
Verify that the expressions obey energy conservation iff $\alpha=\beta=m_2/(m_1+m_2)$.
f) What does this imply for particles of identical masses, $m_1 = m_2$? How does your result fit to the motion observed in Newton's cradle? What does it tell about the assumption of instantaneous collisions of balls that is frequently adopted in theoretical physics?
 ``Free Metal Jacket'' movie poster
``Free Metal Jacket'' movie poster
(wikimedia fair use)}

Dutch Movie poster of Planet Terror.
(wikimedia fair use license)
Problem 3.18:
Inelastic collisions, ballistics, and cinema heroes
Let us take a look at how cinema heroes shoot.
- The title of Stanley Kubrick's movie Full Metal Jacket refers to full metal jacket bullets, i.e., projectiles as they were used in the M16 assault rifle used in the Vietnam war. Its bullets have a mass of $10 \, \text{g}$ and they set a $1 \, \text{kg}$ wooden block revolving at a $1 \, \text{m}$ arm into a $8 \, \text{Hz}$ motion. What is the velocity of the bullets? The bullets of a $9 \, \text{mm}$ Luger pistol have a mass of $8 \, \text{g}$ and they are fired with a muzzle velocity of $350 \, \text{m/s}$. What is the resulting angular speed $\dot\theta$ of the wooden block?
- Alternatively one can preform this measurement by shooting the bullet into a swing where a wooden block of mass $M$ is attached to ropes of length $\ell$. Initially it is at rest. Consider angular momentum conservation to determine its velocity immediately after impact. What does this tell about the kinetic energy immediately after the impact, and what about the maximum height of reached by the swing in its subsequent motion? Let $L$ be $2 \, \text{m}$. Which mass is required to let the swing go up to the height of its spindle?
What does this tell about the recoil of the pistol and the rifle? What do you think now about the shooting scenes that you might recall from Rambo movies or grindhouse movies like Planet Terror.
3.6.2 Mathematical Foundation
Problem 3.19: Solving integrals by partial integration
Evaluate the following integrals by partial integration
\[
\int \mathrm{d} x \, f(x) \, g'(x) = f(x) \, g(x) - \int \mathrm{d} x \, f'(x) \, g(x)
\]
- $\displaystyle \int_a^b {\mathrm{d} x}\, x \, \mathrm{e}^{kx} $
- $\displaystyle \int_a^b {\mathrm{d} x}\, x^2 \, \mathrm{e}^{kx} $
- $\displaystyle \int_0^\infty {\mathrm{d} x}\, x^3 \, \mathrm{e}^{-x^2} $
$\displaystyle \int_a^b {\mathrm{d} x}\, x^n \, \mathrm{e}^{kx} $, $n \in \mathbb{N}$
The integral 4) can only be given as a sum over $j = 0 , \dots , n$.
Problem 3.20: Substitution with trigonometric and hyperbolic functions
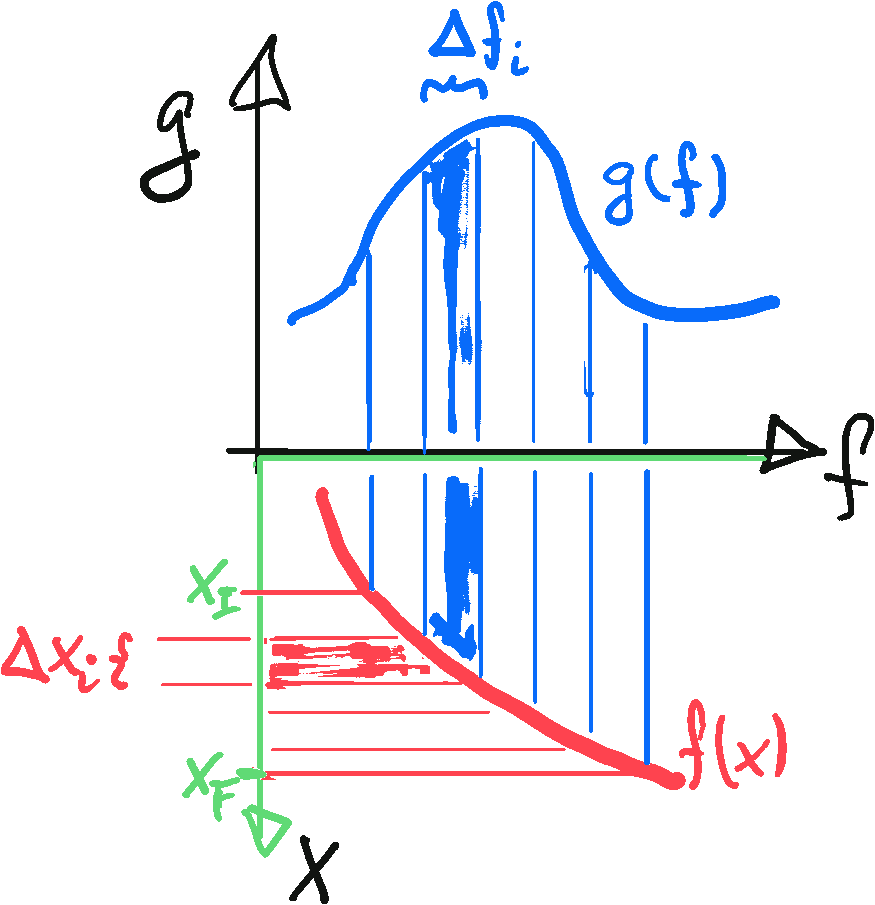 Figure 3.13: Illustration of the substitute rule for integrals that may be represented in terms of a Riemann sum:
\begin{align*}
\int_{f(x_I)}^{f(x_F)} \mathrm{d} f \: g(f)
&\simeq \sum_i \Delta f_i \: g(f_i)
\\
&\simeq \sum_i \Delta x_i \: \frac{ \Delta f_i }{ \Delta x_i } \: g(f(x_i))
\\
&\simeq \int_{x_I}^{x_F} \mathrm{d} x \: \frac{\mathrm{d} f(x)}{\mathrm{d} x} \: g(f(x))
\end{align*}
Figure 3.13: Illustration of the substitute rule for integrals that may be represented in terms of a Riemann sum:
\begin{align*}
\int_{f(x_I)}^{f(x_F)} \mathrm{d} f \: g(f)
&\simeq \sum_i \Delta f_i \: g(f_i)
\\
&\simeq \sum_i \Delta x_i \: \frac{ \Delta f_i }{ \Delta x_i } \: g(f(x_i))
\\
&\simeq \int_{x_I}^{x_F} \mathrm{d} x \: \frac{\mathrm{d} f(x)}{\mathrm{d} x} \: g(f(x))
\end{align*}
Evaluate the following integrals by employing the suggested substitution, based on the substitution rule \[ \int_{f(x_I)}^{f(x_F)} \mathrm{d} f \: g(f) = \int_{x_I}^{x_F} \mathrm{d} x \: \frac{\mathrm{d} f(x)}{\mathrm{d} x} \: g(f(x)) \] with a function $f(x)$ that is bijective on the integration interval $[x_I, x_F]$. A graphical illustration of the rule is given in Figure 3.13.
- $\displaystyle \int_a^b {\mathrm{d} x}\, \frac{1}{ \sqrt{ 1 - x^2 } } $by substituting $x = \sin\theta$
- $\displaystyle \int_a^b {\mathrm{d} x}\, \frac{1}{ \sqrt{ 1 + x^2 } } $by substituting $x = \sinh z$
- $\displaystyle \int_a^b {\mathrm{d} x}\, \frac{1}{ 1 + x^2 } $\by substituting $x = \tan\theta$
- $\displaystyle \int_a^b {\mathrm{d} x}\, \frac{1}{ 1 - x^2 } $\by substituting $x = \tanh z$
Problem 3.21: Gradients and contour lines
a) Contour lines in the $(x,y)$-plane are lines $y(x)$ or $x(y)$ where a functions $f(x,y)$ takes a constant value (cf. Definition 3.7). Sketch the contour lines of the functions
\[
f_1 ( x,y ) = ( x^2 + y^2 )^{-1}
\qquad \text{and} \qquad
f_2( x,y ) = - x^2 \, y^2
\]
b) Determine the gradients $\nabla f_1(x,y)$ and $\nabla f_2(x,y)$.
Hint:
c) Indicate the direction and magnitude of the gradient by appropriate arrows in the sketch showing the contour lines. In which direction is the gradient pointing?
Problem 3.22: Length of the groove of venyl records
DJ Spooky playing venyl records at the Sundance Film Festival (2003), Eddie Codel (Ekai) via Wikimedia Commons, CC BY-SA 3.0
The sound information in venyl records is stored in small undulations of the walls of a groove that runs in a spiral from the outer rim of the disc, at a distance $R_o$ from the centre, towards its center where it stops at a inner radius $R_i < R_o$. Neighboring lanes of the groove have a fixed distance $d$. The sound is picked up by a needle that glides through the groove when the disc is turned. Let $\theta = 0$ be the angle where the needle first touched the disc at time $t_0$, and $\theta(t)$ be the overall traversed angle at time $t \geq t_0$. In the frame of the disc we will denote the position of the needle as \begin{align*} % \label{eq:} \mathbf q (\theta) = R(\theta) \: \hat{\mathbf r}(\theta) \end{align*} Here $\hat{\mathbf r}(\theta)$ is the radial unit vector of polar coordinates taken with respect to the center of the disc, and $R(\theta)$ is the distance from the center.
a) Verify that $R(\theta) = R_a - \varepsilon \: \theta$. What is the relation between $\varepsilon$ and $d$?
b) What is the speed $v$ of the needle while it glides through the groove?
Show that one can express $v$ as follows \begin{align*} % \label{eq:} v = \dot\theta \; \sqrt{ R^2 + f(R) } \end{align*} Determine $f(R)$.
★ c) Demonstrate that the length $L$ of the groove that is traversed while turning from $\theta_I$ to $\theta_E$ can be written as \begin{align*} % \label{eq:} L = \int_i^e \text{d}\theta \: \sqrt{1 + \theta^2} \end{align*} How do $i$ and $e$ depend on $\theta_I$ and $\theta_E$?
d) Observe that \begin{align*} % \label{eq:} \sqrt{1 + \theta^2} = \frac{1}{\sqrt{1 + \theta^2}} + \frac{x^2}{\sqrt{1 + \theta^2}} \end{align*} where the first term is the derivative of $\text{arcsinh}(x)$ and the latter term is related to $\sqrt{1 + \theta^2}$ by partial integration. Use this information to evaluate $L$.
★ e) Compare your result with the following estimate:
- The groove covers an area of size $A = \pi \, R_o^2 - \pi \, R_i^2$.
Why does this hold? How are $R_o$ and $R_i$ related to $\theta_I$ und $\theta_E$? - The area can also be estimated by multiplying the length $L$ of the groove with the groove distance, $d$, such that also $A \approx L\times d$.
How well does the resulting estimate of $L$ agree with the result of the explicit calculation obtained in d).
f) An LP has an outer radius of $R_o = 15\,\text{cm}$ and the groove stops at the inner radius of about $R_i = 8\,$cm. It is played with an angular speed of $33 \frac{1}{3}\,\text{rpm}$ (revolutions per minute), and each side is playing for about $22\,\text{min.}$ What is the length of the groove and what is the distance $d$ between its neighboring revolutions?
3.6.3 Transfer and Bonus Problems, Riddles
Problem 3.22:
Moeschenbroeks double-cone experiment

User:FA2010, Public domain
In the margin we show Moeschenbroeks double-cone experiment.
The setup involves three angles:
1. The opening angle $\alpha$ between the two rails.
2. The angle $\phi$ of the rail surface with the horizontal.
3. The opening angle $\theta$ of the cone.
When it is released from the depicted position the cone might move to the right, to the left, and it could stay where it is. How does the selected direction of motion depend on the choice of the three angles?
Problem 3.23: Coulomb potential and external electric forces
We consider the Hydrogen atom to be a classical system as suggested by the Bohr-Sommerfeld model.
Let the proton be at the center of the coordinate system and the electron at the position $\mathbf r$.
The interaction between the proton and the electron is described by the Coulomb potential $\alpha / |\mathbf r|$.
In addition to this interaction there is a constant electric force acting,
that is described by the potential $\mathbf F \cdot \mathbf r$.
Altogether the motion of the electron is therefore described by the potential
\[
U = - \frac{ \alpha }{ |\mathbf r| } - \mathbf F \cdot \mathbf r
\]
- Sketch the system and the relevant parameters.
- Which force is acting on the particle? How do its equation of motion look like?
- Verify that the energy is conserved.
- Show that also the following quantity is a constant of motion,
\[ I = \mathbf F \cdot \left( \dot{\mathbf r} \times \mathbf L \right) - \alpha \: \frac{\mathbf F \cdot \mathbf r}{|\mathbf r|} + \frac{1}{2} \: \left( \mathbf F \times \mathbf r \right)^2 \] Here $\mathbf L$ is the angular momentum of the particle with respect to the origin of the coordinate system.