Table of Contents
5.1 Motivation and outline: How do particles collide?
In order to get a first impression about this idea we consider the case of two particles at the positions $\mathbf q_i$, $i \in \{1,2\}$ that interact by a repulsive Coulomb force that derives from a potential $\Phi_C(\left\lvert \mathbf R \right\rvert)$ with $\mathbf R = \mathbf q_2 - \mathbf q_1$, \begin{align*} \Phi_C (\left\lvert \mathbf R \right\rvert) = \frac{ C }{ \left\lvert \mathbf R \right\rvert } \quad \Rightarrow \quad \mathbf F_c( \mathbf q_i ) = - \nabla_{\mathbf q_i} \Phi_C( \left\lvert \mathbf q_i - \mathbf q_{2-i} \right\rvert ) = \frac{ C \; \bigl( \mathbf q_i - \mathbf q_{2-i} \bigr) }{ \left\lvert \mathbf q_i - \mathbf q_{2-i} \right\rvert^3 } \end{align*} Here, $2-i$ is the index of the other particle ($1$ for $i=2$ and $2$ for $i=1$), and the constant $C$ is the product of the permittivity of the vacuum and the particle charges. For charges of opposite signs this force has agrees with the gravitational force when one substitutes $C \to -m_1\, m_2\, G$. This results in the same dimensionless equations of motion as obtained for the Kepler problem, with the important difference that the length and time units adopted to defined the dimensionless units take vastly different values. When the two particles carry charges of equal signs the force is repulsive, giving rise to the EOM \begin{align*} 0 = w'' ( \theta ) + w(\theta) + \frac{ \mu \, C }{L^2} \; w( \theta) \end{align*} such that \begin{align*} R (\theta) = \frac{1}{W(\theta)} = \frac { R_0 }{ -1 + \epsilon \: \cos\bigl( \theta - \theta_0 \bigr) } \quad \text{where} \quad R_0 = \frac{L^2}{\mu \, C} \end{align*} agrees with Equation 4.9.3 up to a change of the sign of the one in the denominator and the length unit $R_0$.
Remark 5.1. It is illuminating to adopt a different perspective on the origin of the minus sign in front of the one. Let us write the force on particle $1$ as $\mathbf F_1 = F_1 \: \hat{\boldsymbol e}(\theta)$ where $\hat{\boldsymbol e}(\theta)$ is the vector pointing from particle $1$ to particle $2$. The strength of the scalar force $F_1$ will be positive for an attractive force and negative for a repulsive force. In the dimensionless force $F t_0^2 / \mu\, R_0$ the change of sign is taken into account by the sign of $C$ in $R_0 = L^2 / \mu \, C$ and the solution takes the form of Equation 4.9.3. In order to obtain a positive length scale $\left\lvert R_0 \right\rvert = \pm R_0$ we multiply the numerator and denominator of the solution by the $\pm 1$ and absorb the factor in front of $\epsilon$ in a rotation of the angle by $\pi$ such that the polar coordinates are always aligned with the direction of the force. Hence, one finds \begin{align*} R (\theta) = \frac{1}{W(\theta)} = \frac {\left\lvert R_0 \right\rvert }{ \pm 1 + \epsilon \: \cos\bigl( \theta - \theta_0 \bigr) } \quad \text{where} \quad \pm 1 = \text{sign}\! \left( C \right) \end{align*} At this point dimensionless units play out their strength. We obtain the solution of the nontrivial EOM by an analysis of the ODE and mapping of parameters to a known problem, rather than going again through the involved analysis.
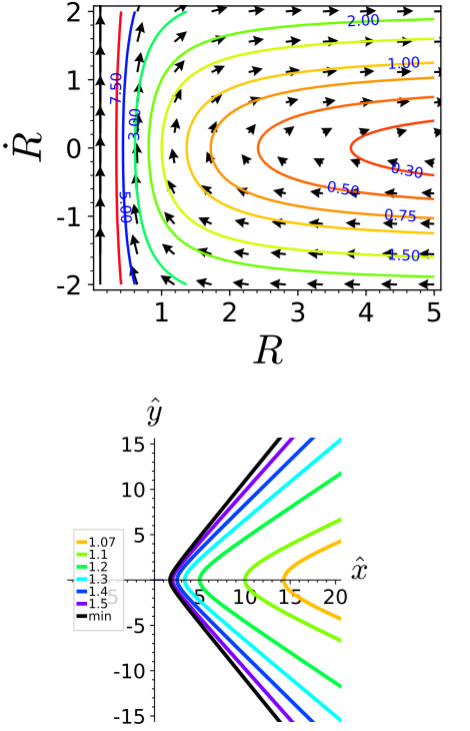
Figure 5.4: Phase-space flow and the shape of trajectories for scattering with a repulsive Coulomb potential.
The phase-space portrait and the shape of the orbits for repulsive interactions are plotted in Figure 5.4. We observe that the trajectory shape describes the approach of the other particle from a perspective of an observer that sits on a particle located in the origin. When the observer sits on a particle that has a much larger mass than the approaching particle, then an outside observer will see virtually no motion of the mass-rich particle and the lines in Figure 5.4 describe the lines of the trajectories of the light particle in a plane selected by the initial angular momentum of the scattering problem. In general, two particles of masses $m_1$ and $m_2$ will be at opposite sides of the center of mass. In a coordinate system with its origin at the center of mass the lines in Figure 5.4 describe the particle trajectories up to factors $m_1/(m_1+m_2)$ and $-m_2/(m_1+m_2)$ for the first and second particle, respectively. A pair of trajectories for $m_1 = 0.3 \, (m_1+m_2)$ and $\epsilon=1.2$ is shown in Figure 5.5. The approximation as point particles is well justified when the sum of the particle radii is much smaller than their closest approach $R_0 / ( \epsilon - 1)$.
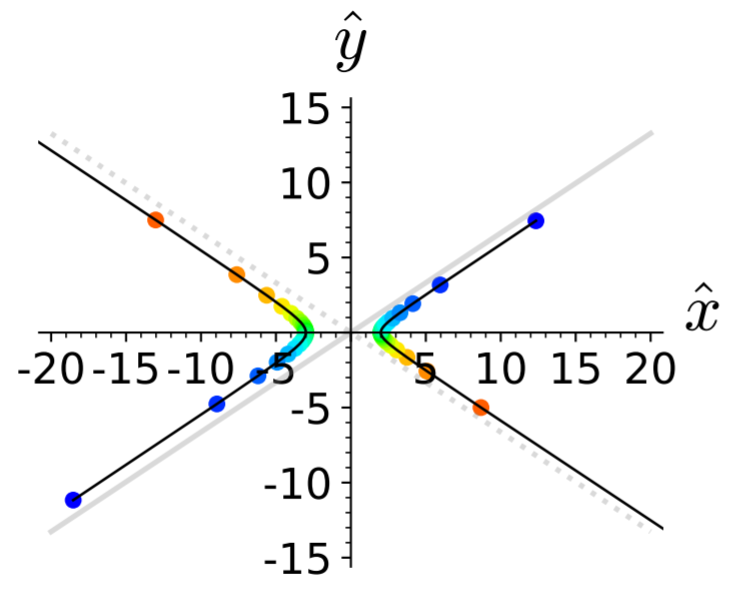
Figure 5.5: The two black lines show the scattering trajectories of two particles with $\epsilon=1.2$ and relative mass $m_1 = 0.3 \, (m_1+m_2)$. They approach each other along the solid gray line and separate along the dotted line. Particle $1$ is initially at the top right. Corresponding positions are marked by dots of matching color.
Outline
In Section 5.2 we study the collision of spherical hard-ball particles that only interact by a force kick vertical to the surfaces at their contact point when they touch. Then we compare the Coulomb case and the force-kick case in order to explore which features of the outgoing trajectories are provided by conservation laws, irrespective of the type of interaction. In Section 5.3 we discuss the forces of an extended object (Earth) on a point particle moving without further interactions in its gravitational field. In Section 5.4 we further explore the impact spatial extension of solid particles: How does their shape matter? How are particles set into spinning motion, and how does the spin evolve? Section 5.5 addresses the motion of particles with internal degrees of freedom. Finally, in Section 5.6 we wrap up the findings of this section by discussing the reflections of balls: How do balls pick up spin in collisions? What happens upon multiple collisions in a channel with parallel walls? How should one return a ping-pong ball arriving with severe spin? How much energy is dissipated into vibrations of the ball?
5.1.1 Self Test
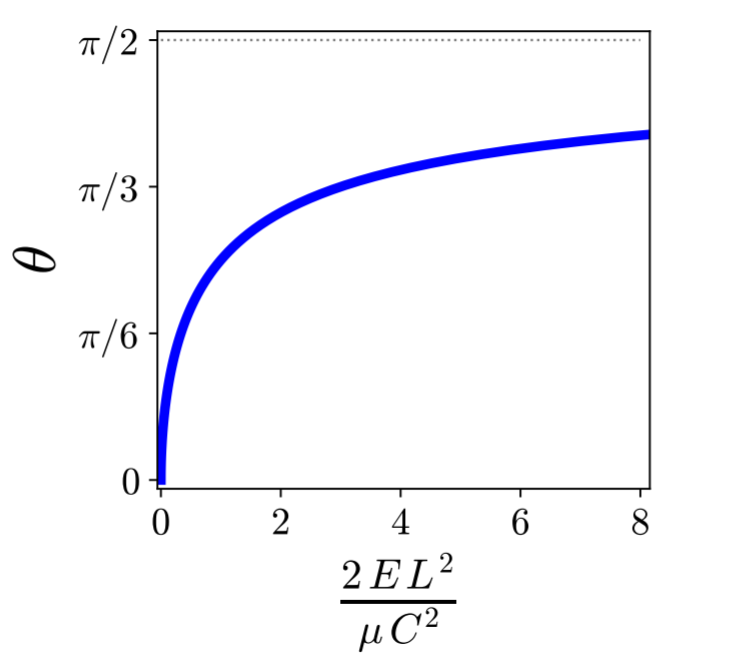
Figure 5.6: Scattering angle $\theta$ for a collision of two particles that interact by a repulsive Coulomb
Problem 5.1: Scattering angle for the Coulomb potential
For the choice of coordinates adopted in Figure 5.4 and Figure 5.5 the trajectories have an asymptotic angle $\theta$ with the $\hat x$-axis when they approach each other and they separate with an asymptotic angle$-\theta$.
a) Show that \begin{align} \tan^2\theta = \frac{ 2\, E\, L^2 }{\mu \, C^2} \tag{5.1.1} \end{align}
b) The parameter dependence of the scattering angle $\theta$ is shown in Figure 5.6.
What happens to the line for very large values of $ 2\, E\, L^2 / \mu \, C^2$?
c) How would the scattering trajectories in Figure 5.5 look like for $\theta = \pi/2$? Does this comply with your finding in b)?