Table of Contents
5.2 Collisions of hard-ball particles
We consider two spherical particles and denote their radii and masses as $R_i$ and $m_i$ with $i \in \{1,2\}$, respectively. At the initial time $t=t_0$ the particles motion is not (yet) subjected to a force such that \begin{align*} \mathbf q_i (t) = \mathbf q_i ( t_0 ) + v_i \: ( t - t_0 ) \, , \quad\text{for}\quad i \in \{1,2\} \end{align*}
5.2.1 Center of mass motion
Analogous to the treatment of the Kepler problem, we decompose the motion of the particles into a center-of-mass motion $\mathbf Q(t)$ and a relative motion $\mathbf r (t)$. Introducing the notion $M = m_1 + m_2$ the former amounts to
\begin{align} M \; \mathbf Q (t) = m_1 \: \mathbf q_1 (t) + m_2 \: \mathbf q_2 (t) = M \: \mathbf Q (t_0) + \dot{\mathbf Q} ( t_0 ) \: ( t - t_0 ) \tag{5.2.1} \end{align} Since there are not external forces the total momentum $M \, \dot{\mathbf Q} (t)$ is conserved (cf. Theorem 3.5) such that Equation 5.2.1 applies for all times – even when the particles collide. A collision will therefore only impact the evolution relative to the center of mass. Equation 5.2.1 holds for all times.
5.2.2 Condition for collisions
To explore the relative motion we write $\mathbf q_i = \mathbf Q + \mathbf x_i$, and we introduce the momentum $\mathbf p = m_1 \: \dot{\mathbf x}_1 = - m_2 \: \dot{\mathbf x}_2$ and the distance coordinate $\mathbf r = \mathbf x_1 - \mathbf x_2$. With these notations the angular momentum of the relative motion reads $ \mathbf L = \mathbf r \times \mathbf p $, and it is conserved when the collision force is acting along the line connecting the centers of the particles (cf. Theorem 3.6 and the discussion of Kepler's problem in Section 4.7). Moreover, $\mathbf r(t)$ is the only time-dependent quantity in this equation because $\mathbf L$ and $\mathbf p$ are preserved. Let us first assume that the particles do not collide, and that the closest approach occurs at some time $t_c$ to a distance $r_c = | \mathbf r(t_c) |$. Then the vectors $\mathbf r(t_c)$ and $\mathbf p$ will be orthogonal, and $|\mathbf L| = r_c \, | \mathbf p |$. By the properties of the vector product the distance of the closest encounter will always be \begin{align*} r_c = \frac{ |\mathbf L| }{ | \mathbf p | } = \frac{ \bigl| m_1 \mathbf q_1(t_0) \times \dot{\mathbf q}_1(t_0) + m_2 \mathbf q_2(t_0) \times \dot{\mathbf q}_2(t_0) - M \mathbf Q (t_0) \times \dot{\mathbf Q} (t_0) \bigr| } { m_1 \bigl| \dot{\mathbf q}_1(t_0) - \dot{\mathbf Q} \bigr| } \end{align*} and there will be no collision if $r_c > R_1 + R_2$.
5.2.3 The collision
Conservation of angular momentum implies that the relative motion of the particles proceeds in a plane.
When they collide they approach until, at time $t_c$,
they reach a position $\mathbf r (t_c)$ where their distance is $|\mathbf r (t_c)| = R_1+R_2$.
We denote the direction of $\mathbf r$ at this time as $\hat{\boldsymbol \beta}$ and augment it by an orthogonal direction $\hat{\boldsymbol \alpha}$
such that $( \hat{\boldsymbol \alpha}, \hat{\boldsymbol \beta}, \hat{\boldsymbol L} = \mathbf L/\left\lvert \mathbf L \right\rvert )$ form an orthonormal basis.
We select the origin of the associated coordinate system such that
\[
\mathbf p
= ( \mathbf p \cdot \hat{\boldsymbol \alpha} ) \: \hat{\boldsymbol \alpha}
+ ( \mathbf p \cdot \hat{\boldsymbol \beta} ) \: \hat{\boldsymbol \beta}
\]
At the collision there is a force $\mathbf F = F \, \hat{\boldsymbol \beta}$ acting on the particles,
that acts in the direction of the line $\mathbf r (t_c)$ connecting the particles.
Hence,
- The momentum component in the $\hat{\boldsymbol \alpha}$ direction is preserved during the collision because there is no force acting in this direction.
- The collision in $\hat{\boldsymbol \beta}$ direction proceeds like a one-dimensional collision, Example 3.12, with the exception that one must retrace the argument using the center-of-mass frame, as discussed in Problem 4.29.
Consequently, we obtain the following momentum $\mathbf p'$ after the collision \[ \mathbf p' = ( \mathbf p \cdot \hat{\boldsymbol \alpha} ) \: \hat{\boldsymbol \alpha} - ( \mathbf p \cdot \hat{\boldsymbol \beta} ) \: \hat{\boldsymbol \beta} = \mathbf p - 2 \; ( \mathbf p \cdot \hat{\boldsymbol \beta} ) \: \hat{\boldsymbol \beta} \]
5.2.4 Self Test
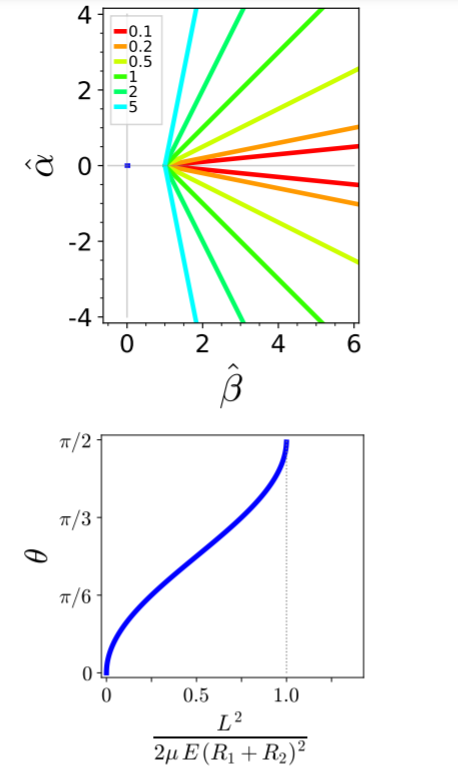
Figure 5.7: Collision of two hard-ball particles with radii $R_1$ and $R_2$: (top) Trajectory shape. The labels denote the ratios $(\mathbf p \cdot \hat{\boldsymbol \alpha}) / (\mathbf p \cdot \hat{\boldsymbol \beta})$. (bottom) Scattering angle $\theta$.
Problem 5.2: Scattering angle for hard-ball particles
In Figure 5.7 we show shows the trajectory shape and the scattering angle for hard-ball scattering.
a) What is the dimensionless length scale adopted to plot the trajectory shapes?
b) What is the impact of the angular momentum on the trajectory shape? What is the impact of the energy?
c) Verify that
\begin{align}
\sin^2\theta = \frac{ L^2 }{2\mu \, E \, (R_1+R_2)^2} \tag{5.2.2}
\end{align}
and that this dependence is plotted in the lower panel of\cref{fig:HardBallScatteringAngle}.
d) What happens when $L^2 > 2\mu \, E \, (R_1+R_2)^2$? Which angle $\theta$ will one observe in that case?
e) 
Problem 5.3: Reflection from a wall
Show that a particle reflected at a flat wall follows the same trajectory
as a particle that collides with a particle of the same mass
and at a position obtained as mirror image of the particle.
Problem 5.4:
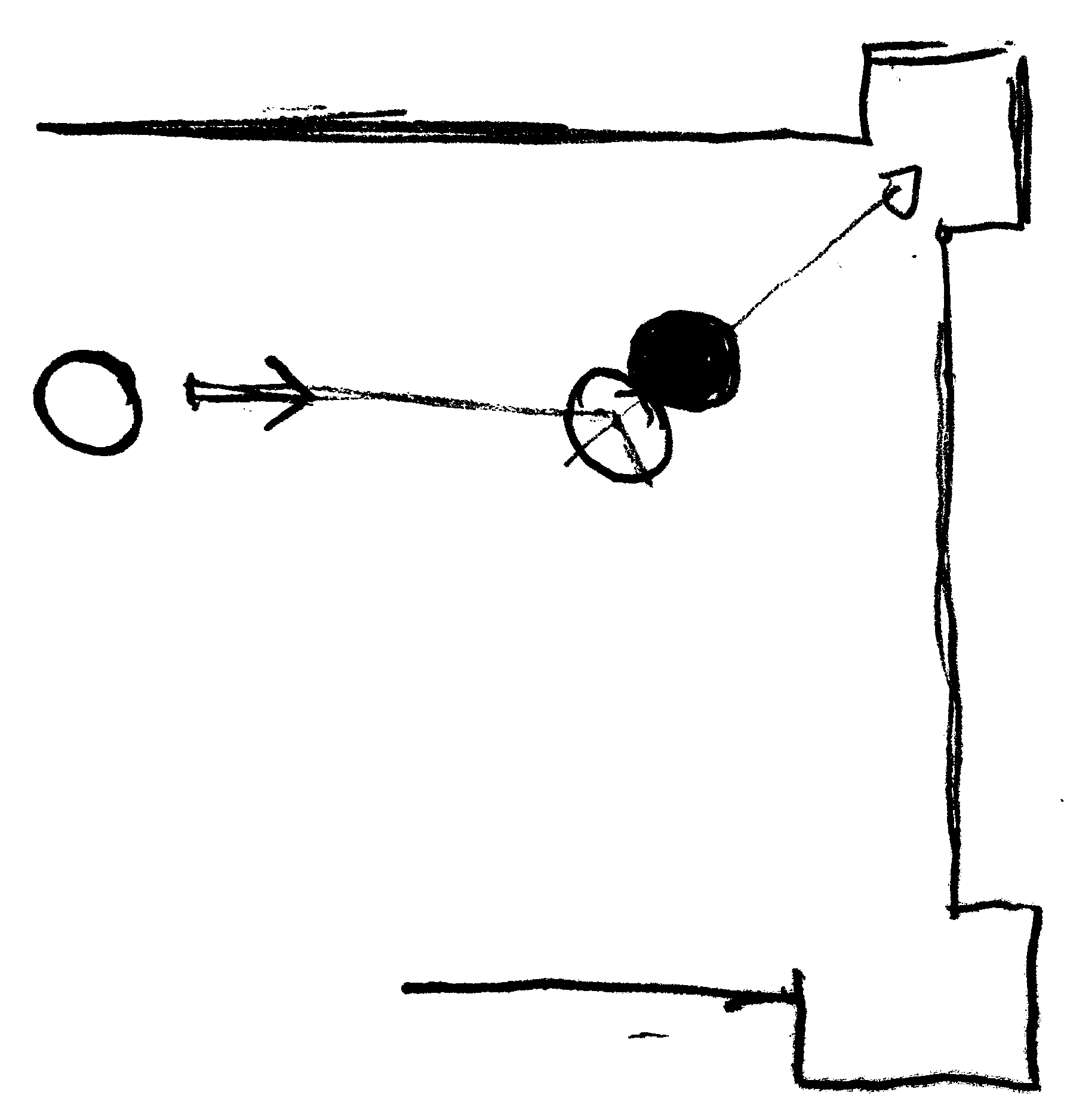
Collisions on a billiard table
The sketch to the right shows a billiard table.
The white ball should be kicked (i.e. set into motion with velocity $\mathbf v$), and hit the black ball such that it ends up in pocket to the top right. What is tricky about the sketched track?What might be a better alternative?