Table of Contents
4.3 Separation of variables — Settling with Stokes drag
The settling of a ball in a viscous medium can be described by the equations of motion \begin{align} m \, \ddot h (t) = -m \, g - \mu \, \dot h (t) \, . \tag{4.3.1a} \end{align} Here $h(t)$ is the vertical position of the ball (height), $g$ is the acceleration due to gravity, and the contribution $-\mu \, \dot h (t)$ describes Stokes friction, i.e., the viscous drag on the ball. It has the same form as the friction opposing the motion of the mine cart in Example 3.6. The Stokes friction coefficient $\mu$ depends the viscosity of the fluid$\eta$ and the geometry of the body. The viscosity $[\eta]$ of a fluid is measured in terms of $ \, \text{Pa} = \, \text{kg/m}\,\text{s}$. For air and water it takes values of about $\eta_{\text{air}} \simeq 2 \times 10^{-5}\, \, \text{kg/m}\,\text{s}$, and $\eta_{\text{water}} \simeq 1 \times 10^{-3}\, \, \text{kg/m}\,\text{s}$, respectively. The size of the ball will be given by its radius $R$. Hence, dimensional analysis implies that \begin{align*} \mu \propto R \, \eta \end{align*} For a sphere of radius $R$ the proportionality constant takes the value of $6\pi$. This problems involves the parameters $g$, $\mu$ and $m$ that will absorbed into dimensionless units by introducing the dimensionless units for height $\hat h = h \, \mu^2 / m^2\, g$, velocity $\hat v = \dot h \, \mu / m\, g$, and time $\tau = (t-t_0) \, \mu / m$. In these units the EOM takes the form
\begin{align} \frac{ \mathrm{d}^2 }{\mathrm{d} \tau^2} \: \hat h(\tau) = -1 - \frac{ \mathrm{d} }{\mathrm{d} \tau} \hat h(\tau) \quad\Leftrightarrow\quad \left\{ \begin{array}{ll} \frac{ \mathrm{d}}{\mathrm{d} \tau}\: \hat h &= \hat v \\ \frac{ \mathrm{d}}{\mathrm{d} \tau}\: \hat v &= -1 - \hat v \end{array}\right . \tag{4.3.1b} \end{align}
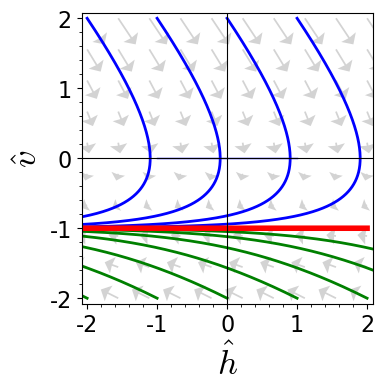Figure 4.5: Dimensionless phase-space trajectories of a particle subjected to a constant acceleration $g$
and Stokes drag.
The corresponding phase-space plot is shown in Figure 4.5. For positive (i.e., upwards) velocities the resulting direction field in phase space point to the lower right, and for $\hat v$ it points straight down. However, the arrows are steeper than for the case without friction, Figure 4.3. For $\hat v > 0$ the trajectories in the two cases look similar, but with friction they follow curves that are broader than the parabola for the frictionless fall. For downwards, the flows differ qualitatively: Trajectories started with zero velocity never cross the $\hat v = -1$ line, and trajectories that are started with a speed larger than $1$ are no longer accelerated by gravity, but slowed down by friction until they also reach their terminal velocity $-1$ that is marked by a red line. After having reached this qualitative insight into the dynamics, we will look now for the explicit solution of the EOM. Equation 4.3.1 can be integrated once, yielding an ODE for the settling velocity starting from a height $\hat h_0$ with velocity $\hat v_0$, \begin{align*} \dot h(\tau) = \hat v_0 - \tau - \bigl( \hat h(\tau) - \hat h_0 \bigr) \end{align*} This equation can not be solved by integration, employing Algorithm 4.1, because its right-hand side explicitly depends on the function $h(t)$ that must still be determined as solution of the ODE. It is a better strategy in this case to adopt another solution strategy.
4.3.1 Solving ODEs by separation of variables
In the case at hand the ODE (4.3.1a) can be interpreted as a first order ODE for the settling velocity $v = \dot h$ where $\dot v$ is provided as a function of only $v$. Such an ODE is best solved by separation of variables.
Algorithm 4.2:Separation of variables
A one-dimensional first-order ODE of the form
\begin{align*}
\dot f (t) = g(f(t)) \, h(t)
\end{align*}
can be solved by separation of variables.
For the initial condition $f(t_0) = f_0$ one obtains then
\begin{align*}
\int_{t_0}^t \mathrm{d} t' \, h(t')
= \int_{t_0}^t \mathrm{d} t' \, \frac{ \dot f(t') }{ g(f(t')) }
= \int_{f_0}^{f(t)} \mathrm{d} f \, \frac{ 1 }{ g(f) }
\end{align*}
which provides the solution in terms of two integrals.
Remark 4.4.
Let us assume that we find the antiderivatives
$H(t)$ with $\mathrm{d} H/\mathrm{d} t = h(t)$
as well as
$A(f)$ with $\mathrm{d} A/\mathrm{d} f = 1/g(f)$ and inverse $I(f)$,
i.e., $I(A(f)) = f$.
Then separation of variables provides the explicit solution
\begin{align*}
H(t) - H(t_0) &= A(f(t)) - A(f(t_0))
\Rightarrow\quad
f(t) &= I\!\bigl( H(t) - H(t_0) + A(f(t_0)) \bigr)
\end{align*}
We will see an example of this type when we resume the discussion of Stokes drag in Section 4.3.2.
Remark 4.5. Often the integrals can be performed but the inverse $I(f)$ can not be given in a closed form. If one can find the inverse of $H(t)$, i.e., a function $J(H)$ with $J(H(t))=t$ then the solution can still be given in the (rather unusual) explicit form \begin{align*} t = J\!\bigl( A(f) - A(f(t_0)) + H(t_0) \bigr) \end{align*} This is always possible for autonomous ODEs, i.e., in particular for Equation 4.3.1a with $f(t)=\dot h(t)$.
Example 4.2 Separation of variable
The solution of the differential equation
\begin{align*}
\frac{\mathrm{d} y(x)}{\mathrm{d} x} = \frac{ \mathrm{e}^{ -y^2(x) } }{ 1+2 \, y^2(x) }
\qquad\text{with}\quad y(0) = 0
\end{align*}
obeys
\begin{align*}
x
= \int_0^x \mathrm{d} x'
= \int_0^{y(x)} \mathrm{d} y \: (1+2\,y^2) \, \mathrm{e}^{ y^2 }
= y(x) \; \mathrm{e}^{ y^2(x) }
\end{align*}
One can not solve this equation to specify $y(x)$,
but it is easy to plot $y \; \mathrm{e}^{ y^2 }$ and swap the axes
(see Figure 4.6).
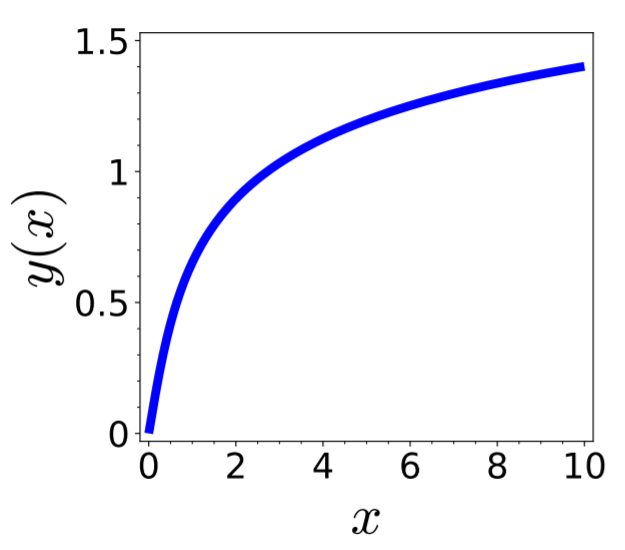Figure 4.6: Solution of the ODE discussed in Example 4.2.
Remark 4.6. When neither of the inverse functions are known, then the solution can only be stated as an implicit equation \begin{align*} H(t) - A(f) = H(t_0) - A(f(t_0)) = \text{const} \end{align*} Hence, the solutions amount to the contour lines of the function $G(t,f) = H(t) - A(f)$ that is plotted to this end as function of the two variables $(t,f)$.1)
Example 4.3 Separation of variable
The solution of the differential equation
\begin{align*}
\frac{\mathrm{d} y(x)}{\mathrm{d} x} = \frac{ y(x) \; \bigl( 1+\cos x) }{ 1 + y(x) }
\qquad\text{with}\quad y(0) = 1
\end{align*}
obeys
\begin{align*}
x + \sin x - 1
&= \int_0^x \mathrm{d} x' \bigl( 1+\cos x' )
\\
&= \int_1^{y(x)} \mathrm{d} y \: \left( \frac{1}{y} + 1 \right)
= \ln y + y - 1
\end{align*}
One can not solve this equation to specify $y(x)$ or $x(y)$. Hence, the solution is given as implicit equation \begin{align*} \Leftrightarrow \quad G(x,y) = y + \ln y - x - \sin x = 0 \end{align*} whose solution is plotted in Figure 4.7.
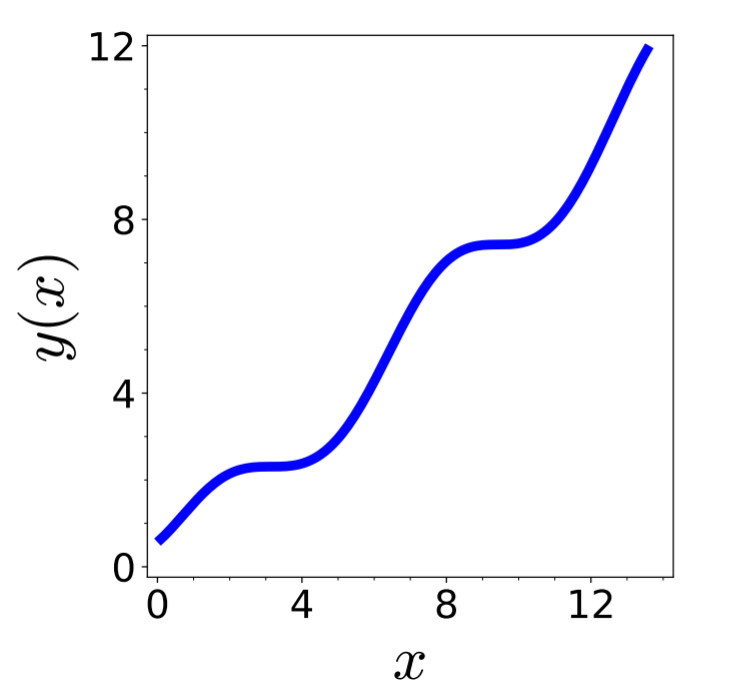Figure 4.7: Solution of the ODE discussed in Example 4.3.
4.3.2 Solving the EOM for settling with Stokes drag
For Equation 4.3.1a we will now derive the velocity $v(t) = \dot h(t)$ for an initial velocity $v_0$ by applying Algorithm 4.2. In order to simplify notations we perform the derivation in dimensionless units, Equation 4.3.1b, and introducing the physical variables in the end. Separation of variables provides that for a particle with initial velocity $\hat v_0$ \begin{align} \tau &= \int_{0}^\tau \mathrm{d} \tau' = - \int_{\hat v_0}^{\hat v(\tau)} \mathrm{d} w \, \frac{1}{ 1 + w } = - \ln\frac{ 1 + \hat v(\tau) }{ 1 + \hat v_0 } \nonumber\\ \Leftrightarrow\quad \hat v(\tau) &= - 1 + \bigl( \hat v_0 + 1 \bigr) \; \mathrm{e}^{-\tau} \tag{4.3.2} \end{align}
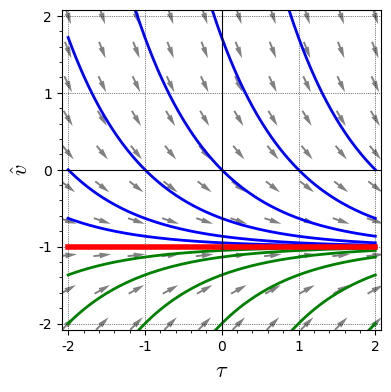Figure 4.8: Sketch of $w(\tau)$ as obtained in Equation 4.3.2.
The solutions are shown in Figure 4.8. Stokes drag entails that for large times, $\tau \gg 1$, the ball is sinking with the constant Stokes velocity that takes the value $-1$ in our dimensionless units. Due to $-1 = \hat v_\infty = \mu v_\infty / m\, g$ this implies $v_\infty = - m\,g / \mu$ in terms of the physical units.
The position of the sphere can be obtained by integrating Equation 4.3.2 for $\hat v(\tau) = \mathrm{d}\hat h / \mathrm{d} \tau$ with initial condition $\hat h_0$, \begin{align}\nonumber \hat h (\tau ) &= \hat h_0 + \int_0^\tau \mathrm{d}\tau \, \frac{ \mathrm{d} h(\tau) }{ \mathrm{d}\tau } = \hat h_0 + \int_0^\tau \mathrm{d}\tau \, \Bigl( - 1 + \bigl( \hat v_0 + 1 \bigr) \; \mathrm{e}^{-\tau} \Bigr) \\ &= \hat h_0 - \tau + \bigl( \hat v_0 + 1 \bigr) \; \left( 1 - \mathrm{e}^{-\tau} \right) \tag{4.3.3a} \end{align} or in terms of physical units \begin{align} h (t) = h_0 - v_\infty \, ( t-t_0 ) + \frac{m}{\mu} \; ( v_0 - v_\infty ) \; \left[ 1 - \exp\left( - \frac{\mu}{m} (t-t_0) \right) \right] \tag{4.3.3b} \end{align}
4.3.3 Relation to free fall
It is instructive to explore how the evolution with Stokes friction is related to the free flight $h_f(t) = h_0 + v_0 (t-t_0) - g\,(t-t_0)^2$ obtained in Section 4.2. This can most effectively be done by Taylor expansion of Equation 4.3.3 for small $\tau$, and subsequently expressing the result in physical units.
Definition 4.4 Taylor expansion
The Taylor expansion to order $N$ provides an approximation of a function $f(x)$ at a position $x_0$.
It is obtained by matching the first $N$ derivatives of the function
and of a polynomial of order $N$ that represents the Taylor approximation
(or Taylor approximation),
\begin{align*}
f(x)
\simeq
\sum_{n=0}^N \left. \frac{\mathrm{d}^n f(x)}{\mathrm{d} x^n} \right\rvert_{x=x_0} \; \frac{ (x-x_0)^n }{n!}
\end{align*}
Remark 4.7: [Leading-order Taylor expansion]
The first-order, or leading-order Taylor expansion is a linear function
$t(x) = t_0 + t_1 x$ with coefficients $t_0 = f(x_0)$ and $t_1 = f'(x_0)$.
Hence, we have $t(x_0) = t_0 = f(x_0)$
and $t'(x) = t_1 = f'(x_0)$.
This is a tangent to the function $f(x)$ that approximates $f$ at $x_0$ by having the same functional value and slope.
Examples for the sine function are shown in Figure 4.9.
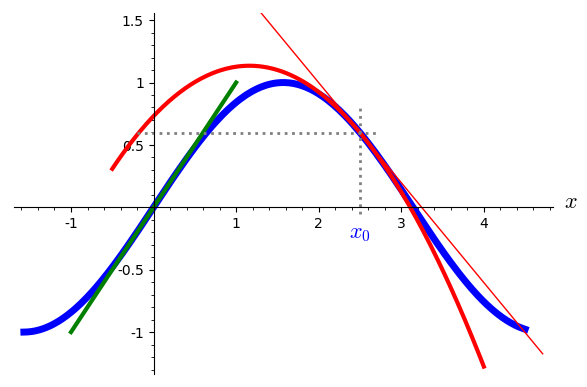Figure 4.9: The leading order and second order Taylor approximations of the sine function
at the origin (green) and at the position $x_0=2.5$.
Remark 4.8. [Second-order Taylor expansion] The second-order Taylor expansion is a quadratic function $t(x) = t_0 + t_1 x + t_2 x^2$ with coefficients $t_0 = f(x_0)$, $t_1 = f'(x_0)$, and $t_2 = f''(x_0)/2$. As for the first-order approximation, we have $t(x_0) = t_0 = f(x_0)$ and $t'(x) = t_1 = f'(x_0)$. Moreover, in this case we also have $t''(x) = 2\,t_2 = f'(x_0)$. Examples for the sine function are shown in Figure 4.9.
Example 4.4 Taylor approximations of the sine function
For $\sin x$ the even derivatives vanish at the origin,
and the odd $2n-1$ derivative amounts to $-1^{n}$.
Hence, the first few
terms of the Taylor expansion at the origin are given by
\begin{align*}
\sin x \simeq x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - \cdots
\end{align*}
At the origin the first and second order Taylor approximation agree,
as shown by the green line in Figure 4.9.
For the sine-function the expansion at a position $x_0$ is given by
\begin{align*}
\sin x
&\simeq
\sin(x_0) \;
\left[ 1 - \frac{(x-x_0)^2}{2!} + \frac{(x-x_0)^4}{4!} - \frac{(x-x_0)^6}{6!} +
\cdots \right]
\\
&+ \cos(x_0) \;
\left[ (x-x_0) - \frac{(x-x_0)^3}{3!} + \frac{(x-x_0)^5}{5!} -
\cdots \right]
\end{align*}
The red lines in Figure 4.9 show
the first-order (thin red line) and
the second order (thick red line) approximation for $x_0=2.5$.
The second order approximation remains closer to the sine-function for a bit longer
than the linear first-order approximation.
Example 4.5 Taylor approximations of the exponential function
The derivatives of the exponential function $f(x) = \exp(a x)$
amount to $f^{(n)}(x) = a^n f(x)$ such that its expansion at a position $x_0$ is given by
\begin{align*}
\mathrm{e}^{a \, x} \simeq \mathrm{e}^{a \, x_0} \; \Biggl[ 1 + a\, (x-x_0) & + \frac{a^2\,(x-x_0)^2}{2} + \cdots
\\
& \qquad
\dots + \frac{a^n \, (x-x_0)^n}{n!} + \cdots \Biggr]
\end{align*}
For $x_0=0$ this simplifies to
\begin{align*}
\mathrm{e}^{a\,x} = \sum_{n=0}^\infty \frac{(a\,x)^n}{n!}
\simeq 1 + a\,x + \frac{(a\,x)^2}{2} + \cdots
\end{align*}
Based on the Taylor expansion of the exponential function $\mathrm{e}^{-\tau} = \sum_{n=0}^\infty (-\tau)^n / n!$ we find for Equation 4.3.3 \begin{align*} \hat h (\tau ) &= \hat h_0 - \tau + \bigl( \hat v_0 + 1 \bigr) \; \left( \tau - \frac{\tau^2}{2} + \frac{\tau^3}{6} - \cdots \right) \\ &= \hat h_0 + \hat v_0\, \tau - \bigl( \hat v_0 + 1 \bigr) \; \frac{\tau^2}{2} \; \left( 1 - \frac{\tau}{3} + \cdots \right) \end{align*} The solution with physical units is obtained by substituting $\hat h = \mu^2 \, h /m^2\,g$, $\hat h_0 = \mu^2 \, h_0 /m^2\,g$, $\tau = \mu \, (t-t_0)/m$, and $\hat v_0 = \mu \, \dot h(t_0) / m \, g$. Hence, \begin{align*} h(t) &= h_0 + v_0 \, (t-t_0) - \frac{\mu}{m} \: \left( v_0 + \frac{m\,g}{\mu} \right) \; \frac{(t-t_0)^2}{2} \; \left( 1 - \frac{\mu \, (t-t_0)}{3 \, m} + \cdots \right) \\ &= h_0 + v_0 \, (t-t_0) - \frac{g}{2} \; (t-t_0)^2 \; \left( 1 - \frac{ v_0 }{ v_\infty } \right) \; \left( 1 - \frac{\mu \, (t-t_0)}{3 \, m} + \cdots \right) \end{align*} This implies that Stokes friction provides a small corrections to the free flight if the initial velocity is small as compared to the asymptotic velocity of free flight, $| v_0 | \ll v_{\infty} = m\,g / \mu$. Further, one must restrict the attention to times that are small as compared to the time scale $m/\mu$ where the asymptotic velocity is reached. Equation 4.3.2 implies that this amounts to situations where the velocity $|v(t)|$ is small as compared to the Stokes settling speed $v_\infty$. This is discussed now for two concrete cases:
Example 4.6 Stokes friction for a steel ball
A steel ball with a diameter of 1 cm has a mass of about \begin{align*} m = \frac{4 \pi}{3} \; 2 \times 10^{3}\, \, \text{kg/m}^3 \; \frac{1 \times 10^{-6}\, \, \text{m}^3}{8} \simeq 1 \times 10^{-3}\, \, \text{kg} \end{align*} In air it will reach a terminal velocity of about \begin{align*} v_{\text{air}} &= \frac{ m \, g }{ \mu_{\text{air}} } = \frac{ 3 \, m \, g }{ 2 \, \eta_{\text{air}} \, R } = \frac{ 3\times 1 \times 10^{-3}\, \, \text{kg} \, 10 \, \text{m/s}^2 }{ 2 \times 2 \times 10^{-5}\, \, \text{kg/m}\,\text{s} \; 1 \times 10^{-2}\, \, \text{m} } \\ &\simeq 7.5 \times 10^{4}\, \, \text{m/s} \end{align*} Saturation to this velocity occurs on time scales \begin{align*} t_{\text{air}} = \frac{m}{\mu_{\text{air}}} = \frac{m}{ \eta_{\text{air}} \, R } = \frac{ 1 \times 10^{-3}\, \, \text{kg} }{ 2 \times 10^{-5}\, \, \text{kg/m}\,\text{s} \; 1 \times 10^{-2}\, \, \text{m} } = 5 \times 10^{3}\, \, \text{s} \end{align*} and this time the bullet will have dropped by a distance $ g\,t_c^2/2 = 2.5 \times 10^{7}\, \, \text{m}$ which is much more than the thickness of the atmosphere. We conclude that Stokes friction is not relevant for the motion of a bullet in air. Even in water, where the viscosity is larger by a factor of $50$, we will have \begin{align*} v_{\text{water}} &= \frac{ 3 \, m \, g }{ 2 \, \eta_{\text{water}} \, R } = \frac{ 3\times 1 \times 10^{-3}\, \, \text{kg} \, 10 \, \text{m/s}^2 }{ 2 \times 1 \times 10^{-3}\, \, \text{kg/m}\,\text{s} \; 1 \times 10^{-2}\, \, \text{m} } \\ &\simeq 1.5 \times 10^{3}\, \, \text{m/s} \end{align*} Saturation to this velocity occurs on time scales \begin{align*} t_{\text{water}} = \frac{m}{ \eta_{\text{water}} \, R } = \frac{ 1 \times 10^{-3}\, \, \text{kg} }{ 1 \times 10^{-3}\, \, \text{kg/m}\,\text{s} \; 1 \times 10^{-2}\, \, \text{m} } = 100 \, \text{s} \end{align*} and this time the bullet will have dropped by a distance $ g\,t_{\text{water}}^2/2 = 5 \times 10^{4}\, \, \text{m}$ which is deeper than the deepest point in our Oceans.2)
Example 4.7 Stokes friction for sperms
Sperms are cells equipped with cilia that allow them to swim towards the egg for fertilization.
They have a characteristic size $L$ of a few micrometers and
they swim in an environment that is approximated here as water.
Their mass is of the order of
$m_{\text{sperms}} = \rho_{\text{water}} \, L^3$.
In this case their asymptotic speed is reached at a time scale
\begin{align*}
t_{\text{spermium}}
&= \frac{m_{\text{spermium}}}{ \mu_{\text{spermium}} }
= \frac{ \rho_{\text{water}} \, L^2 }{ \eta_{\text{water}} }
\\
&= \frac{ 1 \times 10^{3}\, \, \text{kg/m}^3 \; 1 \times 10^{-12}\, \, \text{m}^2 }{ 1 \times 10^{-3}\, \, \text{kg/m}\,\text{s} }
= 1 \times 10^{-6}\, \, \text{s}
\end{align*}
Stokes friction plays a major role for their swimming.
See (Purcell, 1977) for more details.
4.3.4 Self Test
Problem 4.4: Solving ODEs by separation of variables
Determine the solutions of the following ODEs
- $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{\cos^2 y}{\sin^2 x}$ such that $y( \pi/4 ) = 0$
- $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{3 \, x^2 \, y}{2 y^2 + 1}$ such that $y( 0 ) = 1$
- $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = - \frac{1+y^3}{x \, y^2 \, (1+x^2)}$ such that $y(1) = 2$
Problem 4.5: Taylor approximations of the Cosine function
Find the Taylor approximation for the cosine function
- analogously to the discussion in Example 4.4, and
- based on Euler's equation $\mathrm{e}^{\mathrm{i} x} = \cos x + \mathrm{i} \, \sin x$.
Hint:
Problem 4.6: Taylor series
Find the Taylor approximation for the sine function close to
- $x=\pi/4$
- $x=\pi/2$
- $x=3\,\pi/2$
Problem 4.7: Stopping distance of a yacht
A yacht of mass $750 \, \text{kg}$ is sailing on the sailing into the harbor with a speed of $6 \, \text{m/s}$.
At this moment it is experiencing a friction force of $900 \, \text{N}$.
At time $t=0$ the skipper switches off the motor such that only the friction is acting on the boat.
Let the water resistance be proportional to the speed.
- How long will it take till the yacht has come to rest?
- How long will if take till the speed has been reduced to $1.5 \, \text{m/s}$ and which distance has the yacht traversed till that time?
Problem 4.8: Free fall with viscous friction
In Equation 4.3.3 we derived the time evolution of the height$h(t)$ of a ball
that is falling a gravitational field and subjected to Stokes drag.
- Make a plot of $\hat h(\tau)$ as function of $\tau$, where you compare the evolution of trajectories that start with different initial velocity $\hat v_0$ from the same height $\hat h_0 = 0$.
- Make a plot of $h(t)$ as function of $t$, where you compare the evolution of trajectories that start with the same initial velocity $v_0$ from the same height $h_0$, but are subjected to a different drag $\mu$ (for instance because they have different radius).