Table of Contents
4.4 Worked example: Free flight with turbulent friction
In Example 4.6 we reached the puzzling conclusion that — for all physically relevant parameters — Stokes friction plays no role for the motion of a steel ball in air and water. On the other hand, we know from experience that friction arises to the very least for large velocities, like for gun shots. This apparent contradiction is resolved by observing that the drag is not due to Stokes drag. Rather for most settings in our daily live friction arises because the motion of the fluid around the considered object goes turbulent, as anticipated in Problem 3.3. A ball of mass $m$, radius $R$, and mass density $\rho_{\text{ball}}=3m/4\pi\,R^3$ that is moving with speed $v$ through a fluid of mass density $\rho_{\text{fluid}}$ will experience a turbulent drag force of modulus \begin{align} F_D = m \, \frac{\rho_{\text{fluid}} \, C_D}{8 \, \rho_{\text{ball}} \, R} \; v^2 = m \, \kappa \: v^2 \tag{4.4.1} \end{align} Here, $C_D$ is a dimensionless number that typically takes values between $0.5$ and $1$. A very beautiful description of the physics of this equation has been provided in an instruction video of the NASA (click here to check it out). To address motion affected by turbulent drag we measure time in units of $(\kappa g)^{-1/2}$ and velocity in units of $(g/\kappa)^{1/2}$. The dimensionless velocity $\hat v(\tau)$ will then obey the equation of motion
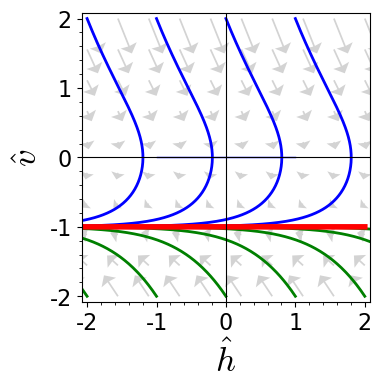 Figure 4.10: Dimensionless phase-space trajectories of a particle subjected to a constant acceleration $g$
and turbulent drag.
Figure 4.10: Dimensionless phase-space trajectories of a particle subjected to a constant acceleration $g$
and turbulent drag.
\begin{align} \frac{\mathrm{d} }{\mathrm{d} \tau} \: \hat h(\tau) &= \hat v \tag{4.2.2a} \\ \frac{\mathrm{d} }{\mathrm{d} \tau} \: \hat v(\tau) &= -1 - \hat v^2(\tau) \: \text{sign}\bigl( \hat v(\tau) \bigr) \tag{4.4.2b} \end{align}
The requirement that the friction force always acts in the direction opposing the motion has been incorporated here by the sign function \begin{align*} \text{sign}(x) = \left\{ \begin{aligned} -1 & \quad\text{for} x<0 \\ 0 & \quad\text{for} x=0 \\ 1 & \quad\text{for} x>0 \end{aligned} \right . \end{align*}
The phase-space flow for this EOM is shown in Figure 4.10. It looks similar to the one for Stokes drag, with the important difference that the change of velocity grows much faster for large $\lvert \hat v \rvert$. For $\hat v > 0$ this gives even rise to an inflection point where the curvature of the trajectories indicated by blue lines crosses from convex to concave. The equation for the velocity can again be solved by separation of variables, \begin{align*} \tau = \int_{0}^\tau \mathrm{d} \tau' = - \int_{\hat v_0}^{\hat v(\tau)} \mathrm{d} w \, \frac{1}{ 1 + w^2 \; \text{sign}\bigl( w \bigr) } \end{align*}
In order to deal with the sign-function, we deal with the integral separately for four types of initial conditions in either of the intervals $\{ (-\infty, -1), [-1,-1], (-1, 0], [0,\infty) \}$. First we consider the initial condition where $\hat v_0 = -1$. In that case $\frac{\mathrm{d}}{\mathrm{d}\tau} w(\tau) = 0$ such that \begin{align} \hat v(\tau) = -1 \qquad\text{for } \hat v_0 = -1 \tag{4.4.3a} \end{align} Next we consider initial conditions where $\hat v_0 < 0$, but $\hat v_0 \neq 0$. In this case
\begin{align}\nonumber \tau &= \int_{\hat v_0}^{v(\tau)} \frac{\mathrm{d} w}{1-w^2} = \frac{1}{2} \: \ln \left( \frac{ 1 - \hat v(\tau) }{ 1 + \hat v(\tau) } \cdot \frac{ 1 + \hat v_0 }{ 1 - \hat v_0 } \right) \\ \Leftrightarrow \;\; \hat v(\tau) &= \left\{ \begin{array}{ll} - \text{tanh}\bigl( \tau - \text{atanh}\, \hat v_0 \bigr) & \quad\text{for } -1 < \hat v_0 \leq 0 \\ \\ - \text{cotanh}\bigl( \tau - \text{acotanh}\, \hat v_0 \bigr) & \quad\text{for } -1 > \hat v_0 \end{array} \right . \tag{4.4.3b} \end{align}
Finally, we consider the case $\hat v_0 > 0$. We expect in that case that the particle moves up, $\hat v(\tau) > 0$, till some time $\tau_c$, and then it start falling due to the action of gravity. However, in that case its velocity heads down with $-1 < \hat v_0 \leq 0$ such that it must follow the solution $\hat v(\tau) = -\text{tanh}( \tau - \tau_c )$ obtained in Equation 4.4.3b. For $\tau<\tau_c$ we find \begin{align*} \tau &= - \int_{\hat v_0}^{\hat v(\tau)} \mathrm{d} w \, \frac{1}{ 1 + w^2 } = - \arctan( \hat v(\tau) ) + \arctan( \hat v_0 ) \\ \Leftrightarrow\quad \hat v( \tau ) &= - \tan\bigl( \tau - \arctan( \hat v_0 ) \bigr) \end{align*} such that
\begin{align} \hat v( \tau ) &= \left\{ \begin{array}{lll} - \tan\bigl( \tau - \tau_c \bigr) & \quad\text{ for } & \hat v_0 > 0 \land \tau < \tau_c = \arctan( \hat v_0 ) \\ - \tanh\bigl( \tau - \tau_c \bigr) & \quad\text{ for } & \hat v_0 > 0 \land \tau \geq \tau_c = \arctan( \hat v_0 ) \tag{4.4.3c} \end{array} \right . \end{align}
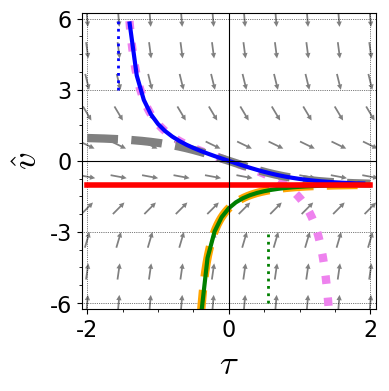 Figure 4.11: Solutions Equation 4.4.3 of Equation 4.4.2a.
Figure 4.11: Solutions Equation 4.4.3 of Equation 4.4.2a.
A solution Equation 4.4.3 that passes through the origin and another one through $(0,-2)$ are shown in Figure 4.11.
4.4.1 Range of applicability
Turbulent friction applies whenever \begin{align*} \mu \, |v| \lesssim m \, \kappa \, v^2 \quad\Leftrightarrow\quad |v| \gtrsim v_c = \frac{\mu}{m \kappa} \simeq \frac{ \eta_{\text{fluid}} }{ \rho_{\text{fluid}} \, R } \end{align*}
For the $1 \: cm$ steel ball considered in Example 4.6 the cross-over velocity $v_c$ yields
\begin{align*} v_c = \left\{ \begin{array}{ll} \frac{ 2 \times 10^{-5}\, \, kg/m s }{ 1 \, kg/m^3 \times 1 \times 10^{-2}\, \, m } = 2 \, mm / s & \quad\text{ for air } \\ \frac{ 1 \times 10^{-3}\, \, kg/m s }{ 1 \times 10^{3}\, \, kg/m^3 \times 1 \times 10^{-2}\, \, m } = 0.1 \, mm / s & \quad\text{ for water } \end{array} \right . \end{align*} Moreover, the characteristic time for turbulent drag is \begin{align*} t_c &= (\kappa g)^{-1/2} = \sqrt{ \frac{ \rho_{ball} \, R}{ \rho_{fluid} \, g } } \\ &= \left\{ \begin{array}{ll} \sqrt{ \frac{ 2 \times 10^{3}\, \, kg/m^3 \times 1 \times 10^{-2}\, \, m }{ 1 \, kg/m^3 \times 10 \, m / s^2 } } \simeq 1.4 \, s & \quad\text{ for air } \\ \sqrt{ \frac{ 2 \times 10^{3}\, \, kg/m^3 \times 1 \times 10^{-2}\, \, m }{ 1 \times 10^{3}\, \, kg/m^3 \times 10 \, m / s^2 } } \simeq 0.04 \, s & \quad\text{ for water } \end{array} \right . \end{align*}
As a consequence, one may safely assume that Stokes friction is always negligible for the steel ball. Either friction may be neglected or turbulent friction must be considered.
4.4.2 Self Test
Problem 4.9:
Turbulent friction
Assume that the Earth atmosphere gives rise to the same turbulent drag, irrespective of height.
- What is the maximum time after which a steel ball that is shot up with vertical velocity $v_0$ will hit the ground?
- Does it make a noticeable difference when you require that $v_0$ must not surpass the speed of light $c = 3 \times 10^{8}\, \, \text{m/s}$?
Problem 4.10:
Free fall with turbulent friction
In Equation 4.4.3 we derived the velocity of a ball that is accelerated by gravity and slowed down by turbulent drag.
- How will the height $\hat h$ of the trajectories evolve for large times $\tau$?
- Determine the full time dependence of the dimensionless height $\hat h$ by solving the ODE $\frac{\mathrm{d}}{\mathrm{d}\tau} \hat h = \hat v$.
Hint: - Make a plot of $\hat h(\tau)$ as function of $\tau$, where you compare the evolution of trajectories that start with different initial velocity $\hat v_0$ from the same height $\hat h_0 = 0$.
- Insert the definitions of the dimensionless units in order to find the solutions for the velocity $v(t)$ and height $h(t)$ in physical units.
Problem 4.11:
Stopping length of a yacht
For moderate speeds1)
a yacht experiences a turbulent drag force of the form given in Equation 4.4.1.
In the following we assume that $\kappa^{-1} \simeq 10 \, \text{m}$.
- The sails of the yacht are shortened at a speed of $v_0=10 \, \text{m/s}$ and some position $x_0$. Subsequently, it is running straight ahead. Determine the position $x(t)$ of the yacht.
- You will find that the yacht never comes to rest. Is that in line with your physical intuition? What might be the origin of this finding?
- What would happen when the yacht is rather subjected to Stokes drag, Equation 4.3.1a, with a friction coefficient of the order of $\mu \simeq R \, \eta = 3 \, \text{m}\, 1 \times 10^{-3}\, \, \text{kg/m s} = 3 \times 10^{-3}\, \, \text{kg/s}$.
- How does the result of c) refer to that of a). Does the comparison help to solve the issue raised in b)?
