6.6 Worked problems: Foucault pendulum
A Foucault pendulum is a mathematical pendulum set up on the Earth surface where we consider only small amplitude oscillations $\theta \ll 1$ with vanishing angular momentum, $C=0$. According to Equation 6.4.11 one expects that it follows the EOM \begin{align} \ddot \theta(t) &= -\frac{g}{\ell} \; \sin\theta(t) \simeq -\frac{g}{\ell} \: \theta(t) \, . \tag{6.6.1} \end{align}
 Remih, CC BY-SA 3.0, via Wikimedia Commons}
Remih, CC BY-SA 3.0, via Wikimedia Commons}
Figure 6.20: Foucault pendulum in the Panthéon, Paris, France.
}
This is a harmonic oscillator with frequency $\omega = \sqrt{g/\ell}$ and solution $\theta(t) = \theta_{\text{max}} \: \sin\bigl( \alpha + \omega \, t \bigr)$. The amplitude $\theta_{\text{max}} \ll 1$ and the offset phase $\alpha$ must be chosen to match boundary conditions. One expects that this motion will be confined to a fixed plane $\varphi=$const. In contrast the plane of motion is turning slowly, and the angular speed of the turning depends on the location where one sets up a Foucault pendulum. This is a striking consequence of the fact that a laboratory on the Earth surface is not an inertial system since it is turning around the Earth axis once every 24 hours.
In order to account for the Earth rotation we adopt spherical coordinates $\hat{\boldsymbol r}(\lambda,\phi)$ with origin at the Earth center and directions indicated by the longitude $\lambda$ and latitude $\phi$ (see sketch in the margin). Earth is rotation around the axis $\hat{\boldsymbol z}$ with a fixed angular frequency $\Omega = 2\pi/24 \, \text{h}$. Hence, $\phi=$const and $\lambda = \Omega\, t$ for a pendulum at a fixed position on the Earth surface. We denote the distance of the pendulum plane from the Earth center as $R$, and the deflection of the pendulum towards the East and North as $x(t)$ and $y(t)$, respectively. Consequently, the position $\mathbf q(t)$ of the pendulum weight amounts to \begin{align*} \mathbf q(t) = R \: \hat{\boldsymbol r} \bigl(\lambda(t), \phi(t) \bigr) + x(t) \: \hat{\boldsymbol \lambda} \bigl(\lambda(t) \bigr) + y(t) \: \hat{\boldsymbol \phi} \bigl(\lambda(t), \phi(t) \bigr) \end{align*}
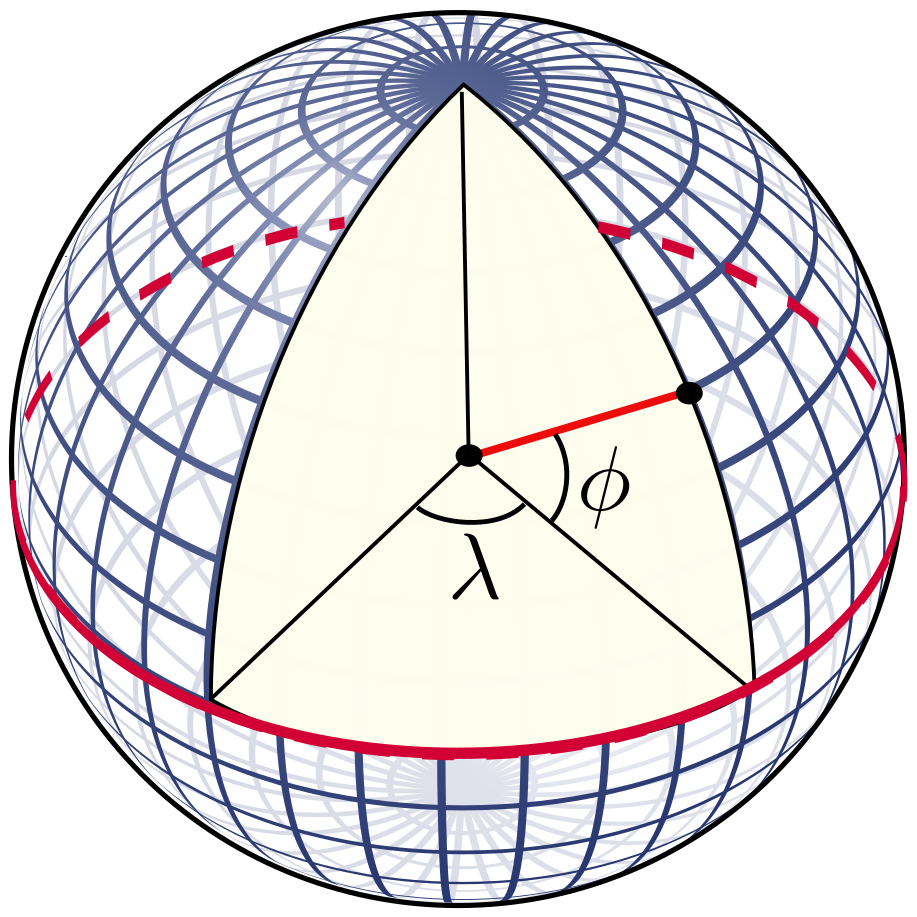
Figure 6.21: Choice of the angles indicating the longitude $\lambda\in\{-\pi/2, \pi/2\}$ and latitude $\phi\in\{-\pi/2, \pi/2\}$ of positions on Earth.}
Therefore, the temporal change of each unit coordinate vector must be orthogonal to $\hat{\boldsymbol z}$,
and it must also be orthogonal to the vector in order to preserve normalization.
Therefore1),
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d} t} \hat{\boldsymbol r} (t) = \Omega \: \hat{\boldsymbol z} \times \hat{\boldsymbol r} (t) \\
\frac{\mathrm{d}}{\mathrm{d} t} \hat{\boldsymbol \lambda}(t) = \Omega \: \hat{\boldsymbol z} \times \hat{\boldsymbol \lambda} (t) \\
\frac{\mathrm{d}}{\mathrm{d} t} \hat{\boldsymbol \phi} (t) = \Omega \: \hat{\boldsymbol z} \times \hat{\boldsymbol \phi} (t)
\end{align*}
and
\begin{align*}
\dot{\mathbf q} = \Omega \: \hat{\boldsymbol z} \times \mathbf q + \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t)
\end{align*}
This provides the Lagrange function as follows the potential energy and the kinetic energy
\begin{align*}
V &= M\, \omega^2 \; \bigl( x^2(t) + y^2(t) \bigr)
\\
T &= \frac{M}{2}\: \dot{\mathbf q}^2
= \frac{M\: \Omega^2}{2} \;\bigl( \hat{\boldsymbol z} \times \mathbf q \bigr)^2
+ M \: \Omega \; \bigl( \hat{\boldsymbol z} \times \mathbf q \bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
+ \frac{M}{2} \; \bigl( \dot x^2 + \dot y^2 \bigr)
\\
&= \frac{M\: \Omega^2 \: \cos^2\phi}{2} \; \mathbf q^2(t)
+ M \: \Omega \; \Bigl( \hat{\boldsymbol z} \times \mathbf q \Bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
+ \frac{M}{2} \; \bigl( \dot x^2(t) + \dot y^2(t) \bigr)
\end{align*}
where we used that
$\lvert \hat{\boldsymbol z} \times \mathbf q \rvert = \lvert \mathbf q \rvert \: \sin\angle(\hat{\boldsymbol z}, \mathbf q) = \lvert \mathbf q \rvert \: \sin\phi$.
Hence, the Lagrange function takes the form
\begin{align*}
\mathcal L &= \frac{M}{2} \; \bigl( \dot x^2(t) + \dot y^2(t) \bigr)
+ M \: \Omega \; \bigl( \hat{\boldsymbol z} \times \mathbf q \bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
\\
&+ \frac{M\: \Omega^2 \: \cos^2\phi}{2} \; \bigl( R^2 + x^2(t) + y^2(t) \bigr)
- \frac{M\, \omega^2}{2} \; \bigl( x^2(t) + y^2(t) \bigr)
\end{align*}
For $x(t)$ we obtain the following contributions to the Euler-Lagrange equation
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d} t} \frac{ \partial \mathcal L }{ \partial\dot x }
&= M \: \ddot x
+ M \: \Omega \; \Bigl[ \bigl(\hat{\boldsymbol z} \times \dot{\mathbf q} \bigr) \cdot \hat{\boldsymbol \lambda}
+ \bigl(\hat{\boldsymbol z} \times \mathbf q \bigr) \cdot \bigl(\hat{\boldsymbol z} \times \hat{\boldsymbol \lambda} \bigr) \Bigr]
\\
&= M \: \ddot x
+ M \: \Omega \: \bigl( \hat{\boldsymbol \lambda} \times \hat{\boldsymbol z} \bigr) \cdot
\bigl( \dot{\mathbf q} - \hat{\boldsymbol z} \times \mathbf q \bigr)
\\
&= M \: \ddot x
+ M \: \Omega \: \bigl( \hat{\boldsymbol \lambda} \times \hat{\boldsymbol z} \bigr) \cdot
\bigl( \dot x \:\hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
\end{align*}
and
\begin{align*}
\frac{ \partial \mathcal L }{ \partial x }
&= M \: \Omega \; \bigl( \hat{\boldsymbol z} \times \hat{\boldsymbol \lambda} \bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
- M\: ( \omega^2 - \Omega^2 \: \cos^2\phi ) \; x(t)
\end{align*}
This provides the EOM
\begin{align*}
\ddot x = 2\, \Omega \; \bigl( \hat{\boldsymbol z} \times \hat{\boldsymbol \lambda} \bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
- ( \omega^2 - \Omega^2 \: \cos^2\phi ) \; x(t)
\end{align*}
Moreover, for $y(t)$ we obtain the same expression up substituting $y(t)$ for $x(t)$ and $\hat{\boldsymbol \phi}$ for $\hat{\boldsymbol \lambda}$,
\begin{align*}
\ddot y = 2\, \Omega \; \bigl( \hat{\boldsymbol z} \times \hat{\boldsymbol \phi} \bigr) \cdot \bigl( \dot x \: \hat{\boldsymbol \lambda}(t) + \dot y \: \hat{\boldsymbol \phi}(t) \bigr)
- ( \omega^2 - \Omega^2 \: \cos^2\phi ) \; y(t)
\end{align*}
Consequently,
\begin{align*}
\begin{pmatrix}
\ddot x \\ \ddot y \\ 0
\end{pmatrix}
&= -2 \: \Omega \, \hat{\boldsymbol z} \times \begin{pmatrix}
\dot x \\ \dot y \\ 0
\end{pmatrix}
- ( \omega^2 - \Omega^2 \: \cos^2\phi ) \: \begin{pmatrix} x \\ y \\ 0 \end{pmatrix}
\end{align*}
Here, we padded the component for the motion in vertical direction by zeros.
Now we observe, that
$\hat{\boldsymbol z} = \sin\phi \: \hat{\boldsymbol r} + \cos\phi \: \hat{\boldsymbol \phi}$
and we observe that the contribution to of $\cos\phi \: \hat{\boldsymbol \phi}$ to the cross product
will give rise to a vector in $\hat{\boldsymbol r}$ direction,
which we do not consider here.
Consequently,
\begin{align*}
\begin{pmatrix}
\ddot x \\ \ddot y
\end{pmatrix}
&= -2 \: \Omega\,\sin\phi \: \begin{pmatrix}
-\dot y \\ \dot x
\end{pmatrix}
- ( \omega^2 - \Omega^2 \: \cos^2\phi ) \: \begin{pmatrix} x \\ y \end{pmatrix}
\end{align*}
This EOM is most transparently solved by introducing the complex variable
$z = x + \mathrm{i} \, y$, and observing that
$-\mathrm{i} \dot z = -\dot y + \mathrm{i}\, \dot x$.
Hence,
\begin{align*}
\ddot z
= \ddot x + \mathrm{i} \ddot y
= 2\, \mathrm{i} \: \Omega\,\sin\phi \: \dot z
- ( \omega^2 - \Omega^2 \: \cos^2\phi ) \: z
\end{align*}
This linear, homogeneous differential equations in solved by superpositions of exponential functions,
$\exp(\gamma\, t)$
where $\gamma$ obeys the characteristic equation
\begin{align*}
0 &= \gamma^2 - 2\, \mathrm{i} \: \Omega\,\sin\phi \: \gamma + ( \omega^2 - \Omega^2 \: \cos^2\phi )
\\
\Rightarrow\quad
\gamma_\pm &= \mathrm{i} \: \Omega\,\sin\phi \pm \mathrm{i}\: \sqrt{ \Omega^2\,\sin\phi^2 + \omega^2 - \Omega^2 \: \cos^2\phi }
\\
&= \mathrm{i} \: \left(\Omega\,\sin\phi \pm \sqrt{ \omega^2 - \Omega^2 \: \cos(2\phi) } \right)
\\
&\simeq \pm\mathrm{i} \, \omega + \mathrm{i} \, \Omega\,\sin\phi
\end{align*}
with corrections to the frequency $\omega$ that are smaller to the leading order by a factor of $(\omega/\Omega)^2$.
The Foucault pendulum is started at a position $z(t_0)$ with velocity $\dot z(t_0)$.
For this initial condition we obtain the solution
\begin{align*}
z(t) = z_0 \: \exp\bigl(\mathrm{i} \: (\Omega\,\sin\phi)\: (t-t_0)\bigr) \; \cos\bigl( \omega\, (t-t_0) \bigr)
\end{align*}
The phase factor of $z_0 \in \mathbb C$ accounts for the initial orientation of the displacement.
The evolution of the phase factor $\exp\bigl(\mathrm{i} \: (\Omega\,\sin\phi)$ induces a rotation of the plain of motion
with a frequency of $\Omega\,\sin\phi$.
At the poles this rotation entails that the orientation of the oscillation is fixed for an outside observer,
while the Earth rotates underneath.
At the equator there is no rotation.
At mid latitudes one observed a rotation frequency of $\Omega\,\sin\phi$.
Note that the sine factors entails that the Foucault pendulum moves clockwise on the Northern hemisphere
and counter-clockwise on the Southern hemisphere.
