4.1 Motivation and outline: EOM are ODEs
From the mathematical point of view the equation of motion is an ordinary differential equation (ODE).
Definition 4.1 Ordinary Differential Equation (ODE)
An ordinary differential equation (ODE) of $n^{\text{th}}$ order
for a function $f(t)$ expresses the $n^{\text{th}}$ derivative of the function,
\begin{align*}
f^{(n)}(t) = \frac{\mathrm{d}^n}{\mathrm{d} t^n} f(t)
\end{align*}
as a function of time and the lower derivatives of the function,
$f^{(n-1)}(t)$, $\dots$,
$f^{(1)}(t) = \frac{\mathrm{d}}{\mathrm{d} t} f(t)$,
$f^{(0)}(t) = f(t)$,
\begin{align*}
f^{(n)}(t) = F( f^{(n-1)}(t), \dots, f(t) , t ) \, .
\end{align*}
Here, $f$ and $F$ may be scalar or vector valued functions.
Remark 4.1. The EOM for a particle at position $\mathbf q \in \mathbb{R}^3$ is a second order ODE where the second time derivative $\ddot{\mathbf q}(t)$ of the vector valued function $\mathbf q(t)$ (the position of the particle) is related to $\mathbf F/m$, which is a vector that depends on $\dot{\mathbf q}$, $\mathbf q$ and $t$; cf Definition 3.3.
Remark 4.2. A differential equation is called an ordinary differential equation, when all derivatives are taken with respect to the same variable. When discussing the physics of waves, e.g., for the full description of Tsunami waves mentioned in Example 1.11, to deal with electromagnetic waves or gravitational waves, one has to deal with differential equations involving space and time derivatives. These type of equations are called partial differential equations (PDE). In Leipzig they are addressed in the course “Theoretical Physics II”.
Commonly, the forces in an EOM for a particle only depend on particle positions and velocities, and not explicitly on time. The forces only depend on the particle configuration, and they will be the same irrespective of whether I measure them today or when my grand-daughter determines them with her grand-children at the dawn of the next century.
Definition 4.2 Autonomous Equations of Motion
An ODE is called autonomous
when its right-hand side does not explicitly depend on time.
In particular an autonomous EOM takes the form
\begin{align*}
m \: \ddot{\mathbf q}(t) = \mathbf F( \dot{\mathbf q} (t), \mathbf q (t) ) \, .
\end{align*}
The forthcoming discussion of ODEs makes use of the very important observation that every ODE can be stated as first order ODE in some abstract phase space. We introduce this idea for $N$ particles with masses $m_i$, $i=1\cdots N$ that are moving in $D$ dimensions. According to Definition 3.3 their motion is described by a system of $N\,D$ differential equations for the coordinates of the $D$ dimensional vectors $\mathbf q_i = ( q_{i,\alpha} , \alpha = 1\cdots D )$ \begin{align*} \ddot{q}_{i,\alpha} & = \frac{1}{m_i} \; F_{i,\alpha}( \{ \dot{\mathbf q}_i , \mathbf q_i \}_{i=1\cdots N}, t ) \, , \quad i=1\cdots N \, , \;\; \alpha=1\cdots D \end{align*} To avoid clutter in the equations we did not explicitly state here the time dependence of $\ddot{q}_{i,\alpha}(t)$, $\dot{q}_{i,\alpha}(t)$, and ${q}_{i,\alpha}(t)$. By introducing the variables $\mathbf v_i = \dot{\mathbf q}_i$ the EOMs can be written as a set of $2\,D\,N$ first order ODEs \begin{align*} \dot q_{i,\alpha} &= v_{i,\alpha} \\ \dot v_{i,\alpha} & = \frac{1}{m_i} \; F_{i,\alpha}( \{ \mathbf q_i, \dot{\mathbf q}_i \}_{i=1\cdots N}, t ) \end{align*} For an autonomous system this can be written in a more compact form by introducing the $2DN$ dimensional phase-space coordinate $\boldsymbol\Gamma$ and the flow $\boldsymbol{\mathcal{V}}$ as follows \begin{align*} \boldsymbol\Gamma &= \bigl( q_{1,1} \cdots q_{1,D} \, , \; q_{2,1} \cdots q_{N,D} \, , \; \dot q_{1,1} \cdots \dot q_{1,D} \, , \; \dot q_{2,1} \cdots \dot q_{N,D} \bigr) \\ \boldsymbol{\mathcal{V}} &= \left( v_{1,1} \cdots v_{1,D} \, , \; v_{2,1} \cdots v_{N,D} \, , \; \frac{F_{1,1}}{m_1} \dots \frac{F_{1,D}}{m_1} \, , \; \frac{F_{2,1}}{m_2} \cdots \frac{F_{N,D}}{m_N} \right) \\ \dot{\boldsymbol\Gamma} &= \boldsymbol{\mathcal{V}} ( \boldsymbol\Gamma ) \qquad \text{for autonomous systems.} \end{align*} Moreover, a non-autonomous system can always be expressed as an autonomous, first order ODE where $\boldsymbol\Gamma$ and $\boldsymbol{\mathcal{V}}$ denote points in a $2DN+1$ dimensional phase space, \begin{align*} \boldsymbol\Gamma &= \bigl( q_{1,1} \cdots q_{1,D} \, , \; q_{2,1} \cdots q_{N,D} \, , \; \dot q_{1,1} \cdots \dot q_{1,D} \, , \; \dot q_{2,1} \cdots \dot q_{N,D} \, , \; t \bigr) \\ \boldsymbol{\mathcal{V}} &= \left( v_{1,1} \cdots v_{1,D} \, , \; v_{2,1} \cdots v_{N,D} \, , \; \frac{F_{1,1}}{m_1} \dots \frac{F_{1,D}}{m_1} \, , \; \frac{F_{2,1}}{m_2} \cdots \frac{F_{N,D}}{m_N} \, , \; 1 \right) \\ \dot{\boldsymbol\Gamma} &= \boldsymbol{\mathcal{V}} ( \boldsymbol\Gamma ) \qquad \text{for non-autonomous systems.} \end{align*} In phase space, $\boldsymbol\Gamma$ denotes a point that characterizes the state of our system, and $\boldsymbol{\mathcal{V}}( \boldsymbol\Gamma )$ provides the unique direction and velocity of the temporal change of this state. In an approximation, that is accurate for sufficiently small $\Delta t$, we have \begin{align*} \boldsymbol\Gamma( t + \Delta t ) \simeq \boldsymbol\Gamma( t ) + \Delta t \; \boldsymbol{\mathcal{V}} ( \boldsymbol\Gamma (t) ) \end{align*} In phase space the ODE therefore can be represented as a field of vectors $\boldsymbol{\mathcal{V}}( \boldsymbol\Gamma )$ that represent signposts signifying which direction a trajectory will take when it continues from this point, and how fast it will proceed.
Definition 4.3 Phase-Space Plot
A phase-space plot provides an overview of all solutions of an ODE by marking the direction of motion of the trajectories in phase space by arrows,
and showing the evolution of a representative set of trajectories by solid lines.
At times such a plot is therefore also denoted as the phase-space portrait of the solutions of an ODE.
Remark 4.3. For an autonomous system with a single DOF \begin{align*} \dot x (t) = v (t) \\ \dot v (t) = m^{-1} \: F\bigl( v(t), x(t) \bigr) \end{align*} the phase-space portrait is a two-dimensional plot with arrows $\bigl( v, F( v, x )/m \bigr)$ at the positions $(x,v)$ in the plane, and trajectories $v(x)$. One can only see the shape of the trajectories, and not their time dependence.
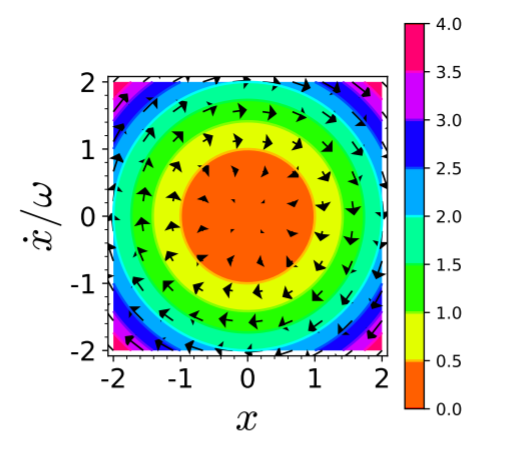 Figure 4.1: Color plot of contour lines of the energy of the harmonic oscillator,
and the flow field of its EOM.
Figure 4.1: Color plot of contour lines of the energy of the harmonic oscillator,
and the flow field of its EOM.
Example 4.1 Phase-space plot for the harmonic oscillator
The EOM of the harmonic oscillator is $\ddot x(t) = -\omega^2 \, x(t)$
where $\omega$ can be absorbed into the time scale by adopting the dimensionless time $\tau=\omega t$.
Its dimensionless energy is then given by
\begin{align*}
E = \frac{v^2}{2} + \frac{x^2}{2}
\quad
\text{with}
\left\{
\begin{array}{ll}
\dot x &= v \\
\dot v &= -x
\end{array} \right.
\end{align*}
The energy is conserved because
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d} t}E = x\,\dot x + v\, \dot v = x\,v - v\,x = 0
\end{align*}
Therefore trajectories in phase space amount to contour lines of the the energy function $E(x,v)$.
This is shown in Figure 4.1
where the energy is marked by color coding and the direction of the flow is provided by arrows.
Outline
The forthcoming discussion in the present chapter will provide
- i. a classification of ODEs with an emphasis on strategies to find solutions for specific initial conditions, and
- ii. further discussion of phase-space plots used to characterize sets of solutions.
The methods will be introduced and motivated based on elementary physical problems that will serve as examples of particular relevance in physics.
