Theoretical Mechanics IPSP

Problem 6.16: Two masses hanging at a rubber band
Two weights of the same mass $m$ are attached on opposite ends of a rubber band that is hanging over a roll. The weights are at height $h_1$ and $h_2$. They move only vertically, either one up and one down at a fixed length of the band, or stretching the band, or releasing tension on the band. We assume that friction and the mass of the band are negligible.

a) Sketch the problem, and indicate the relevant parameters and coordinates.

b) We describe the problem by adopting the coordinates $H = h_1+h_2$ and $D = h_1 - h_2$. Verify that the Lagrange function will then take the following form \[ \mathcal L ( H, D, \dot H, \dot D ) = \frac{\mu}{2} \, \left( \dot H^2 + \dot D^2 \right) - mg \, H - \frac{k}{2} \, H^2 \] Here $k$ is the elastic module of the rubber band, and $\mu$ is an effective mass. How is $\mu$ related to $m$? The expression for the $\mathcal L$ adopts a particular choice of the origin used to specify $h_1$ and $h_2$. Which choice has been used?

c) Determine the equations of motion for $H$ and $D$.

d) Solve the equations of motion and interpret the result. For which values of $H$ and $D$ will you trust the result?

Problem 6.17: Kitchen pendulum
We consider a pendulum that is built from two straws (length $L_1$ and $L_2$), two corks (masses $m_1$ and $m_2$), a paper clip, and some Scotch tape (see picture to the right). It is suspended from a shashlik skewer, and its motion is stabilized by means of the spring taken from a discharged ball-pen. Hence, the arms move vertically to the skewer. We denote the angle between the arms as $\alpha$, and the angle of the right arm with respect to the horizontal as $\theta(t)$.

1. Determine the kinetic energy, $T$, and the potential energy, $V$, of the pendulum. Argue that $T$ and $V$ can only depend on $\theta$ and $\dot\theta$, and determine the resulting Lagrangian $\mathcal{L}(\theta, \dot\theta)$.
2. Determine the EOM of the pendulum.
3. Find the rest positions of the pendulum, and discuss the motion for small deviations from the rest positions. Sketch the according motion in phase space.
4. The EOM becomes considerably more transparent when one selects the center of mass of the corks as reference point. Show that the center of mass lies directly below the fulcrum when the pendulum it at rest.
5. Let $\ell$ be the distance of the center of mass from the fulcrum, and $\varphi(t)$ be the deflection of their connecting line from the vertical. Determine the Lagrangian $\mathcal{L}(\varphi, \dot\varphi)$ and the resulting EOM for $\varphi(t)$.
6. Do you see how the equations for $\ddot\theta(t)$ and $\ddot\varphi(t)$ are related?

Problem 6.18: The driven pendulum
We consider a (mathematical) pendulum of mass $m$ with a pendulum arm of length$\ell$. The deflection of the arm with respect to its rest position is denoted as $\theta(t)$. The fulcrum of the pendulum is moving vertically, residing at the position $z(t)$ at time $t$.

1. Sketch the setup of for this problem, and mark the relevant physical parameters and coordinates.
2. Determine the kinetic energy $T$ and the potential energy $V$ of the pendulum mass.
3. We assume that the mass of the pendulum arm does not play a significant role for the motion. Use the Lagrange formalism to determine the equation of motion for $\theta$. Can you imagine why $\ddot\theta(t) = 0$ for $\ddot z = -g$?
4. Discuss the stability of the fixed points of the motion for $\ddot z > -g$ and $\ddot z < -g$. Sketch corresponding phase-space plots for constant $\ddot z$.
5. Consider now the $T$-periodic motion with

\begin{align*} z (t) = \left\{ \begin{array}{lll} a \, t \, (t - T/2 ) & \quad\text{ for} & 0 < t < T/2 \\ a \, ( T - t ) \, (t - T/2 ) & \quad\text{ for} & T/2 < t < T \end{array} \right . \end{align*} What does this imply for $\ddot z$? How would the trajectories close to $\theta = 0$ and $\theta = \pi$ look like for $a>g$?

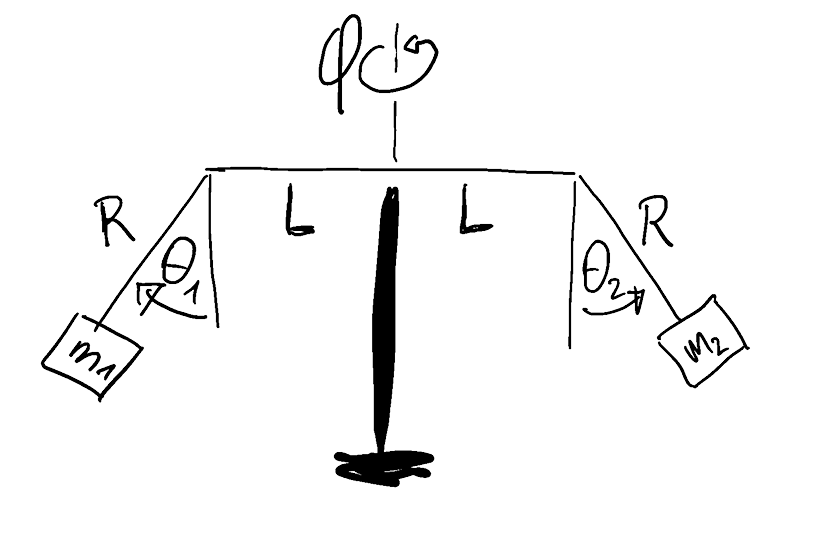
Problem 6.19: Freely rotating carousel

We consider a carousel with two arms of length$R$ that are attached to cantilevers of length$L$. The arms can swing outwards and inwards, and we assume that they move without friction and can take full turns. Their outwards deflection will be denoted as $\theta_1(t)$ and $\theta_2(t)$, respectively. At time $t$ the cantilever turns towards the direction $\varphi(t)$ in the horizontal plane. We consider free rotation; there is no external driving controlling the evolution of $\varphi$. We describe the system in cylinder coordinates, $\hat{\boldsymbol r}$, $\hat{\boldsymbol z}$ and $\hat{\boldsymbol \varphi}$, with $\hat{\boldsymbol z}$ aligned antiparallel to gravity $\mathbf g$.

a) Provide a sketch to illustrate that the positions $\mathbf q_i$ of mass $i \in \{ 1, \:2 \}$ can be expressed as, \begin{align*} \mathbf q_i &= (L + R \: \sin\theta_i ) \; \hat{\boldsymbol r} - R \: \cos\theta_i \: \hat{\boldsymbol z} \, , \end{align*} and take the derivative to show that \begin{align*} \dot{\boldsymbol q_i} &= R\, \dot\theta_i \: \cos\theta_i \: \hat{\boldsymbol r} + (L + R \: \sin\theta_i ) \; \dot\varphi \; \hat{\boldsymbol \varphi} + R \, \dot\theta_i \: \sin\theta_i \: \hat{\boldsymbol z} \, . \end{align*}

b) Establish the kinetic energy, $T$, the potential energy $V$, and the Lagrange function.

c) Verify that $\varphi$ is a cyclic variable and show that the associated conserved quantity takes the form \begin{align*} K = f( \theta_1, \theta_2 ) \: \dot\varphi \end{align*} Provide the explicit form of $f( \theta_1, \theta_2 )$.

d) Determine the equations of motion for $\theta_i(t)$, and select an appropriate time scale (the same for both angles!) such that \begin{align*} \ddot\theta_i = - \sin\theta_i + \frac{k^2}{\bigl( f(\theta_1,\theta_2) \bigr)^2 } \: \cos\theta_i \: \left( \lambda + \sin\theta_i \right) \end{align*} Which time scale has been adopted? How do $k$ and $\lambda$ depend on the masses, lengths scales, and $K$?

e) We have found that the dynamics of $\theta_1$ and $\theta_2$ are coupled due to the appearance of $f(\theta_1,\theta_2)$. Compare this dynamics of the angles to the case where the rotation frequency $\dot\varphi$ is controlled by a motor — like for a carousel. How does the coupling differ? What does this imply for the time evolution?

f) The discussion of the coupled dynamics is too involved for the exam. In the following we therefore consider the case where no weight is attached to arm two (i.e.$m_2=0$). Show that $f(\theta_1,\theta_2)$ will then be proportional to $\left( \lambda + \sin\theta_1 \right)^2$. Show that this implies that \begin{align*} \ddot\theta_1 = - \sin\theta_1 + \frac{\kappa^2}{ \left( \lambda + \sin\theta_1 \right)^\nu } \: \cos\theta_1 \end{align*} What is the relation between $\kappa$, $k$, and the system parameters? Which value do you find for the value of $\nu$?

g) Show that the dynamics is governed by an effective potential \begin{align*} U_{\text{eff}}(\theta_1) = -\cos\theta_1 + \frac{ c }{ \left( \lambda + \sin\theta_1 \right)^2 } \end{align*} Determine the constant $c$ in this expression.

h) When $\lambda$ is large the prefactor of the $\cos\theta_1$ is almost constant. Sketch the phase-space dynamics!

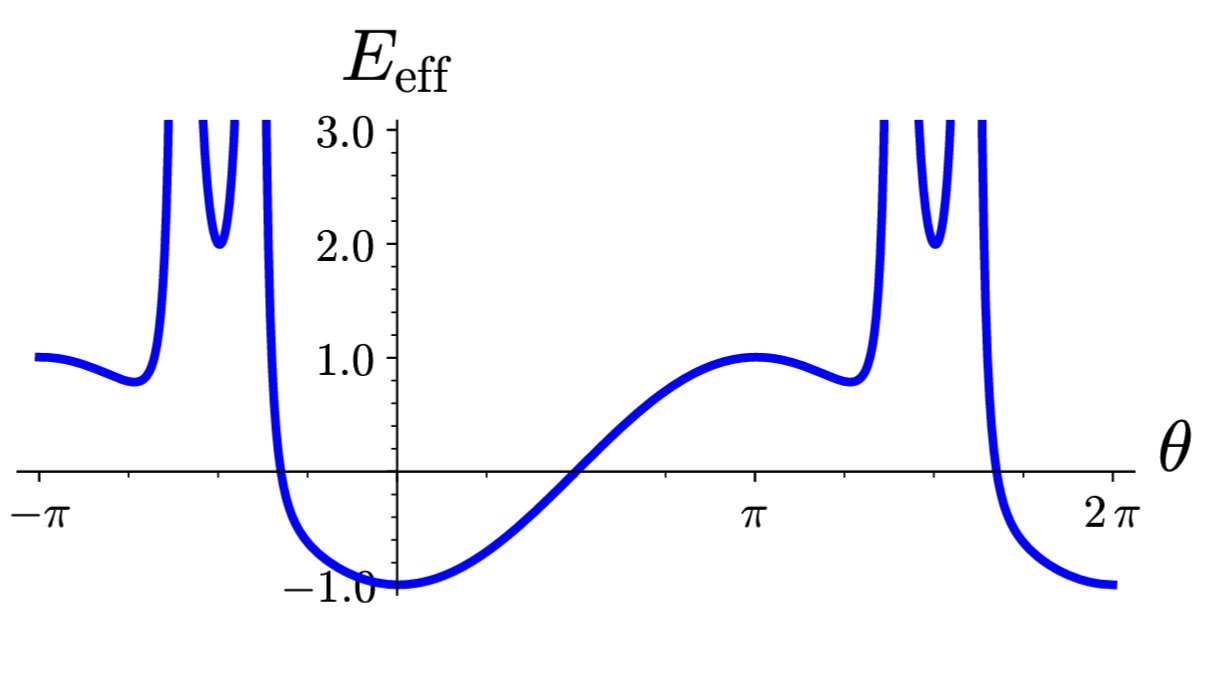
i) For all $\lambda < 1$ the dynamics in phase-space changes dramatically, no matter how small one chooses $\kappa$. For instance the following graph shows the effective potential for $\kappa = 0.1$ and $\lambda = 0.95$.

Sketch the phase-space dynamics for this parameter value.

Bonus: How does the arm move close to the stable fixed points? Why does the effective potential change so dramatically for $\lambda < 1$? What is the physical origin of this change?

j) Finally we consider the case of two equal masses on a carousel with $\lambda \gg 1$. Further we consider the situation where the two masses are oscillating more or less in phase such that $\theta_1 = \theta + \delta$ and $\theta_2 = \theta - \delta$ with $\delta \ll 1$. Show that the equations of motion can then be approximated as \begin{align*} \ddot\theta \pm \ddot\delta = -\cos\theta \mp \delta \: \sin\theta + \frac{\kappa^2}{2} \: \frac{ ( \lambda + \sin\theta ) \pm \delta \: \cos\theta }{ \left( \lambda + \sin\theta \right)^{4} } \end{align*} Take the sum and the difference of the two equations to show that $\theta$ evolves in the same way as for the case where only one mass was attached, while \begin{align*} \ddot\delta \simeq -\delta \; \left( \sin\theta - \frac{\kappa \: \cos\theta}{ \left( \lambda + \sin\theta \right)^{4} } \right] \end{align*} What does this imply when $\theta$ resides at the fixed point $\theta_c$ where also $\theta_c \ll 1$.

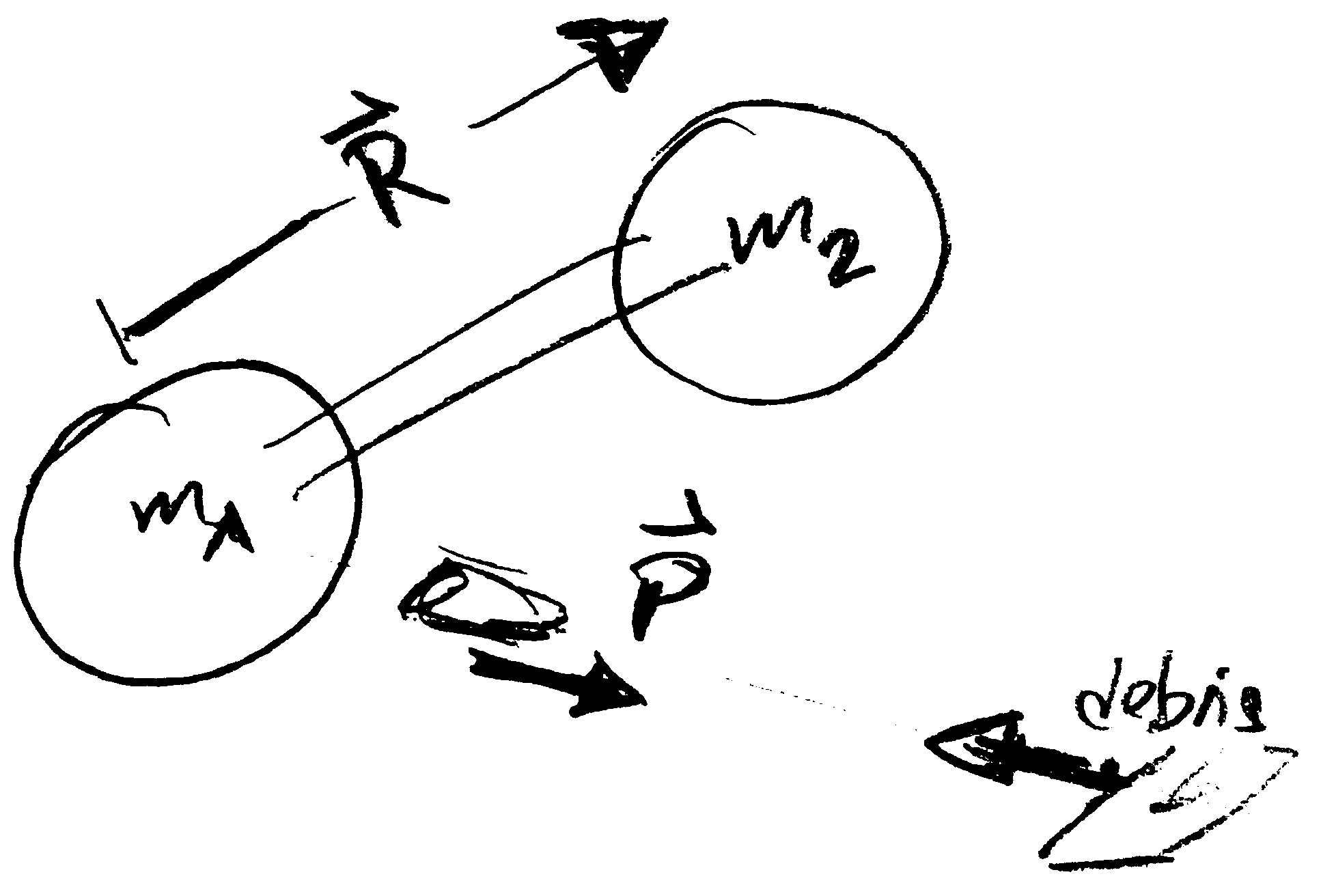
Problem 6.20: Space-station lost

We consider a cluster of two coupled space stations (masses $m_1$ and $m_2$) that are connected by a supply channel whose mass may be neglected as compared to $m_1$ and $m_2$. The supply channel takes the form of a stiff tube that cannot bend. However, it is attached to the stations in such a way that the distance $R$ between the stations may change; with a restoring force $-k\,(R-\ell)$ towards the rest length $\ell$. We consider an emergency where one of the stations is approached by a heavy piece of space debris (\cf sketch in the margin). To prevent damage the debris is intercepted by a space torpedo that leaves the endangered station with momentum $\mathbf P$. We choose a coordinate frame where the station is at rest initially. How will it move after launching the torpedo? We approach the problem by first determining the equations of motion of the coupled space stations. Subsequently, we discuss the situation at hand.

a) Determine the center of mass $\mathbf Q$ of the coupled space stations, and its equation of motion. Before launching the torpedo the center of mass is at rest at the origin of our coordinate system. How does it move after the launch?

b) The launch of the torpedo induces a torque that leads to a rotation of the coupled space stations. We will now discuss this rotation in their center of mass frame, i.e., we discuss the evolution of the vector $\mathbf R(t)$ that describes their orientation in space. Show that the angular momentum $\mathbf L = \mathbf R(t) \times \mu \dot{\mathbf R}(t)$ is preserved.

c) Why does this imply that the coupled space station will rotate in the plane defined by the initial position of $m_1$ and $m_2$, and the approaching piece of debris?

d) Determine the Lagrange function for the motion of $\mathbf R$ in the plane selected by angular-momentum conservation, and determine the equation of motion for$\mathbf R (t)$.

e) Show that the conservation of energy $E$ and the modulus of angular momentum imply that \[ E = a \dot R^2 + \frac{b}{R^2} + c \, R^2 - d\, R + e \] and determine the positive real constants $a$, $b$, $c$, $d$, and $e$ in terms of the masses $m_1$ and $m_2$, the rest length $\ell$ of the supply channel, strength $k$ of the restoring force, and the angular momentum $|\mathbf L| = L$.

f) Determine the effective potential $\Phi_{\text{eff}}(R)$ for the evolution of the distance $R (t)$, and sketch the solutions of its equation of motion in phase space.

g) Mark the initial condition of $R(t)$ in the phase-space plot, i.e.its value and speed immediately after launch of the torpedo, and discuss the entailed evolution of$\mathbf R(t)$.

h) How does the minimum energy required to stop its rotation depend on the direction of approach of the debris?

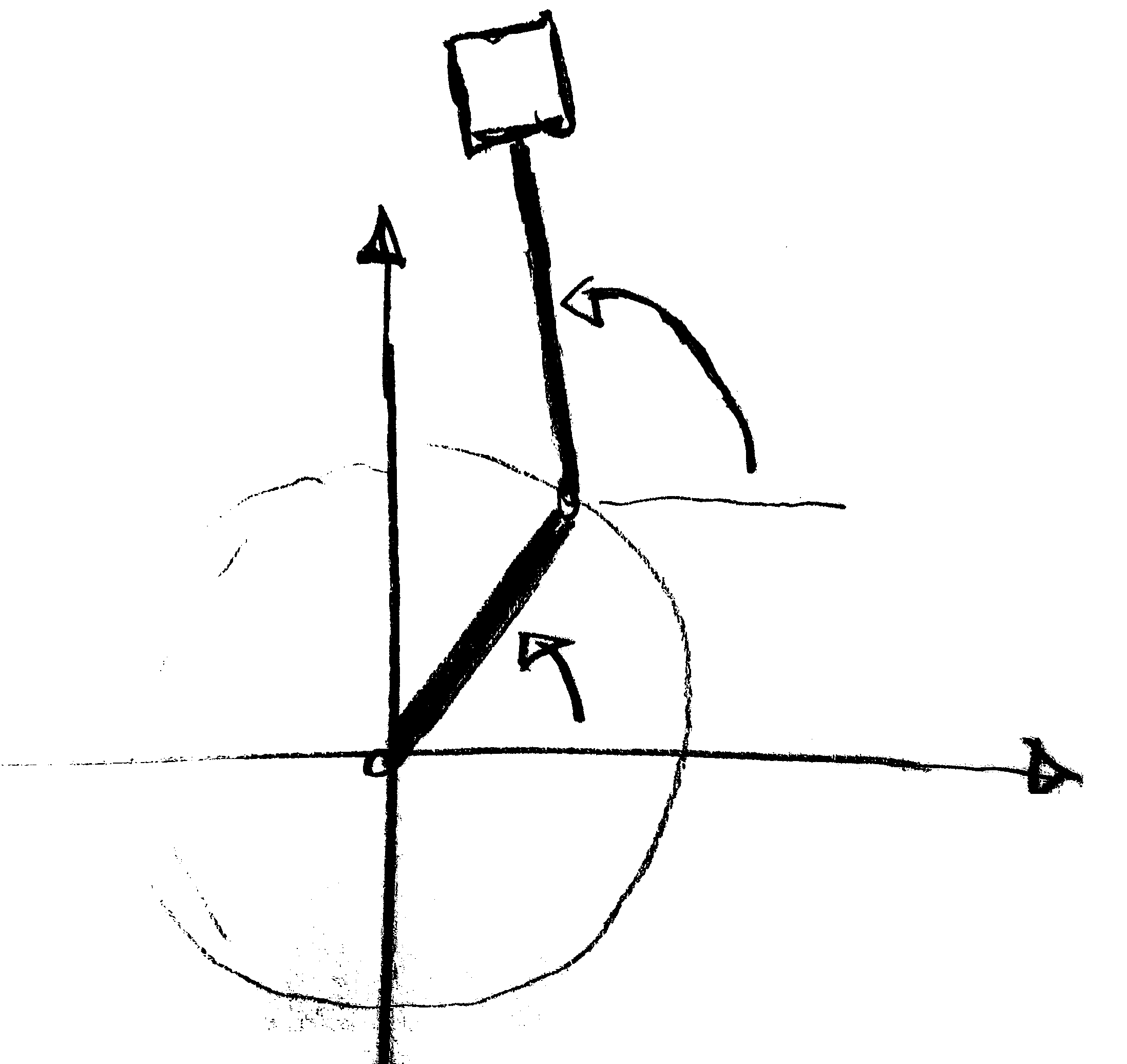
Problem 6.21: Horizontal driven double pendulum
A double pendulum is a mathematical pendulum with another pendulum attached to its loose end (see sketch). We will consider here a horizontal double pendulum where the arms run in a horizontal plane perpendicular to gravity. Moreover, we will control the position of the outer pendulum by a motor such that the angle between the $x$-axis and the outer arms revolves with with a fixed, constant frequency $\Omega$.

a) Label the quantities in the sketch:

The pendulum is moving in the $(x,y)$ plane. How is gravity oriented?
The inner arm has length $R$. Its fixed end lies in the origin of the $(x,y)$-plane, and it is pointing in direction $\theta(t)$ with respect to the positive $x$ axis.
The outer arm has a length $L$. It connects the loose end of the inner arm and a weight of mass$M$. The angle between this arm and the $x$-axis is $\Omega t$.

b) Consider the vectors $\hat{\mathbf{r}} (\phi) = \hat{\mathbf{x}} \: \cos\phi + \hat{\mathbf{y}} \: \sin\phi$ and $\hat{\mathbf{\phi}} (\phi) = \frac{\mathrm{d}}{\mathrm{d}\phi} \hat{\mathbf{r}}(\phi)$. Show that for each value of $\phi$ they form an orthonormal pair of unit vectors in the $(x,y)$-plane.

c) Express the position $\mathbf q$ of the weight with respect to the origin as a linear combination of $\hat{\boldsymbol{r}} (\theta)$ and $\hat{\boldsymbol{r}} (\Omega t)$; i.e.determine $a$ and $b$ such that \begin{align*} \mathbf q(t) = a \: \hat{\boldsymbol{r}} (\theta) + b \: \hat{\boldsymbol{r}} (\Omega t) \\ \end{align*}

d) Determine $\mathbf{\dot q}(t)$ and the kinetic energy of the horizontal driven double pendulum.

e) Determine (i) the potential energy, (ii) the Lagrange function, and (iii) the equation of motion for $\theta(t)$.

f) Show that – with an appropriate choice of the time scale – the dimensionless equation of motion for $\alpha(t) = \theta(t) - \Omega \, t$ takes the form \begin{align*} \ddot \alpha (t) = - \sin \alpha(t) \\ \end{align*} Which time scale was chosen to obtain this result?

g) Show that $\displaystyle E = \frac{\dot\alpha^2}{2} - \cos\alpha$ is a constant of motion.

h) Determine the stable and unstable fixed points of the equation of motion. Sketch its solutions in phase space.

i) The results of f) and g) imply that $\alpha(t)$ behaves like a mathematical pendulum. Interpret its solutions:

• Which motion of the double pendulum is described by the stable fixed points?
• Which track does the double pendulum follow for closed trajectories around a stable fixed point?
• Which motion is described the the unstable fixed points?
• How do trajectories look like where $\dot\alpha$ never changes its sign?
• How does the system's homoclinic trajectory look like in terms of $\theta(t)$?

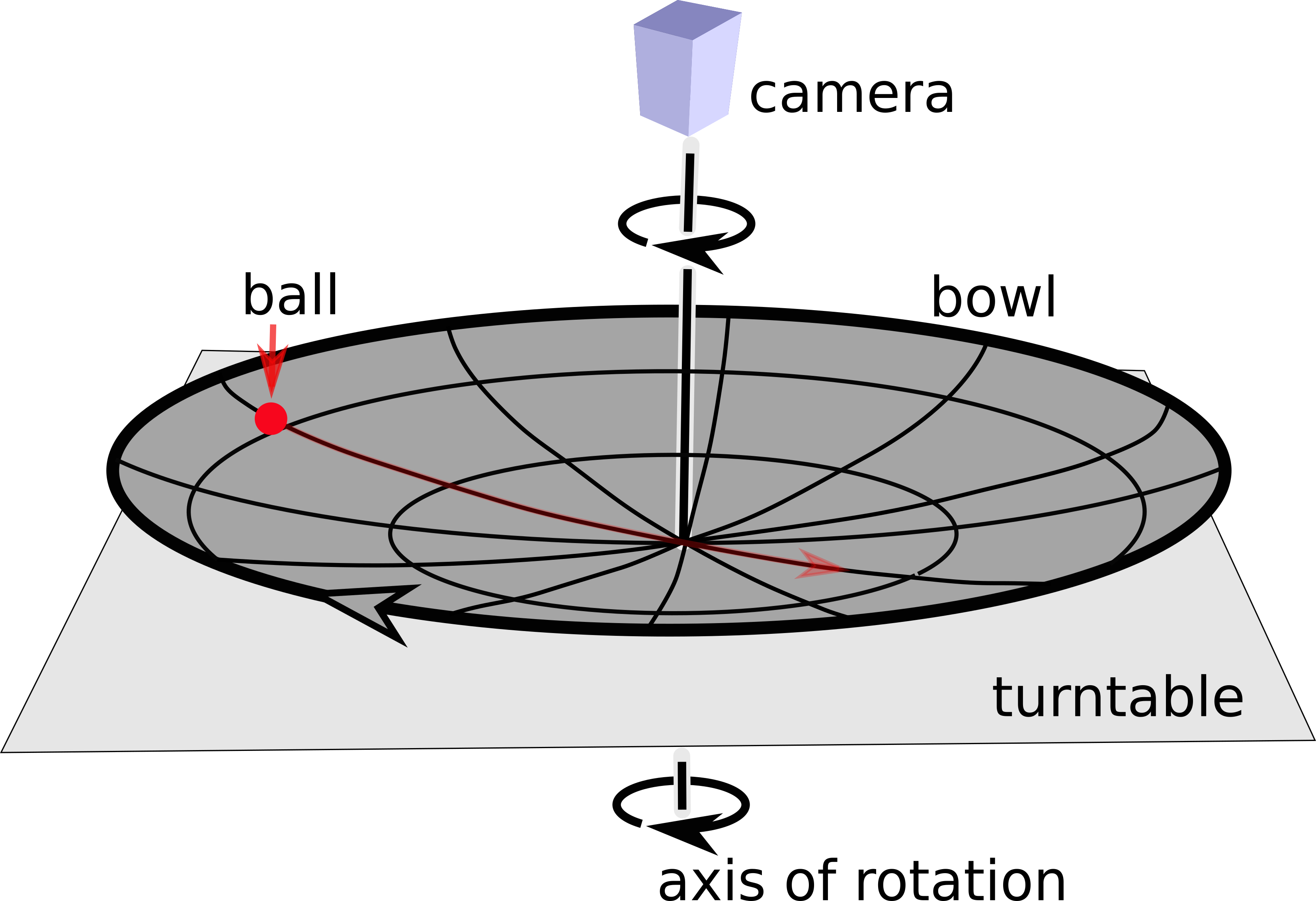
Problem 6.22: Coriolis forces on the turntable

The effect of Coriolis forces on a particle can beautifully be described by the motion of a ball moving in bowl placed on a turntable (\cf sketch in the margin). Let $m$ be the mass of the ball, $\Omega$ the rotation frequency of the turntable, and $z(r)$ the cylinder-symmetric height profile of the bottom of the bowl, as function of the distance$r$ from the rotation axis. We will disregard effects due to friction and the rolling of the ball.

a) We select a bowl with a height profile that gives rise to a harmonic force $\mathbf F = -k \mathbf r$ towards the center of the turntable, and we choose $\Omega$ such that the centripetal force balances the force $\mathbf F$. Determine $\Omega$.

b) First, we describe the motion of the ball from the perspective of an observer standing at rest next to the turntable. The position of the ball is specified by the complex number $r(t)$, that describes the distance to the rotation axis. Show that the motion of the ball takes the form of an ellipse
\begin{align*} r(t) = A \, \mathrm{e}^{\mathrm{i} ( \theta + \phi)} \; \mathrm{e}^{ \mathrm{i} \Omega t } + B \, \mathrm{e}^{\mathrm{i} ( \theta - \phi)} \; \mathrm{e}^{- \mathrm{i} \Omega t } \, , \qquad \text{with\ } \theta, \phi, A, B \in \mathbb{R} \, . \end{align*} How are the parameter of the ellipse related to $\theta$, $\phi$, $A$, and $B$?

c) Now, we describe the motion of the ball from the perspective of a camera that is mounted on the turntable, and follows the motion in the frame of reference moving with the turntable. In this case we describe the position of the ball by the complex number $q(t)$. Demonstrate that the equations of motion take the form \begin{align*} \frac{\delta^2 \mathbf q(t)}{\delta t^2} = -2 \Omega \, \mathrm{i} \, \frac{\delta \mathbf q(t)}{\delta t} \, . \end{align*} Determine the solution of this equation.

d) At time $t_0$ we release the ball with velocity $\dot r(t_0) = 0$ at the position $r(t_0) = R \in \mathbb{R}$. Determine the resulting solutions $r(t)$ and$q(t)$. How are the solutions related?

Problem 6.23: Shortest path on a sphere
We describe the position on the surface of a three-dimensional sphere by the angle$\theta$ with its ``North pole'', and the azimuthal angle$\varphi$ in the horizontal plane. A trajectory on the sphere with radius $R$ can then be specified as $\mathbf q(t) = R \: \hat{\boldsymbol r}\! \bigl( \theta(t), \varphi(t) \bigr)$, or alternatively by $\theta(\varphi)$ or $\varphi(\theta)$. We will now derive conditions for a path of extremal length on the sphere.

a) Without restriction of generality we restrict our discussion to spheres with unit radius, $R=1$. Why is this admissible?

b) Show that the length of the path from $\bigl( \theta(t_i), \varphi(t_i)\bigr) = (\theta_i, \varphi_i)$ to $\bigl(\theta(t_e), \varphi(t_e)\bigr) = (\theta_e, \varphi_e)$ amounts to \begin{align*} L = \int_{t_i}^{t_e} \mathrm{d} t \: \Bigr\lvert \dot{\hat{\boldsymbol r}}\! \bigl(\theta(t), \varphi(t) \bigr) \Bigr\rvert &= \int_{\varphi_i}^{\varphi_e} \mathrm{d}\varphi \; \sqrt{ \sin^2\theta(\varphi) + \left( \frac{\mathrm{d} \theta(\varphi)}{\mathrm{d}\varphi} \right)^2 } \\ &= \int_{\theta_i}^{\theta_e} \mathrm{d}\theta \; \sqrt{ 1 + \sin^2\theta \, \left( \frac{\mathrm{d} \varphi(\theta)}{\mathrm{d}\theta} \right)^2 } \end{align*} Under which conditions do the expressions apply? Why and when do they provide the same length?

c) A necessary condition for the extremality of $L$ is that the variation $\delta L$ vanishes for the integrals that have been defined in (b). Introduce the variation $\theta(\varphi) + \varepsilon\, \delta\theta(\varphi)$ into the second representation of the length (i.e., the one involving an integral over $\varphi$), calculate $\delta L$, and determine the resulting differential equation for paths $\theta(\varphi)$ of extremal length.

d) Repeat the same steps for the variation $\varphi(\theta) + \delta\varphi(\theta)$ and the representation of the length in terms of $\varphi(\theta)$. Determine the resulting differential equation for paths $\varphi(\theta)$ of extremal length. Which derivation is simpler? How could you have seen this before performing the calculations?

e) The result of (d) can be integrated once. Show that this results in the following first order differential equation \begin{align*} \frac{\mathrm{d} \varphi}{\mathrm{d}\theta} = \frac{\cos\alpha}{\sin\theta} \; \left[ \sin^2\alpha - \cos^2\theta \right]^{-1/2} \, . \end{align*} where $\sin\alpha$ is an integration constant.

f) Verify that the following function is a solution of the differential equation \begin{align*} \varphi(\theta) = \varphi_0 - \text{arcsin}\! \frac{\cos\alpha \; \cos\theta }{ \sin\alpha \; \sin\theta } \, . \end{align*} Hint: Express $\sin(\varphi-\varphi_0)$ as a function of $\theta$. Take the $\theta$ derivative of both sides of the equation. Subsequently, you can determine $\varphi'(\theta)$ by eliminating $\cos(\varphi-\varphi_0)$ by means of the known expression for $\sin(\varphi-\varphi_0)$.

g) Show that all the coordinates \[ \mathbf q(\theta) = ( \sin\theta \, \cos\varphi(\theta), \sin\theta \, \sin\varphi(\theta), \cos\theta ) \] of the trajectory obtained in (f) are orthogonal to the vector $( 0, \sin\alpha, \cos\alpha )$.
Then: How does the path look like on the sphere?

h) The path from the initial point to the final point on the sphere is not unique! One of the solutions is the shortest path on the sphere. What type of an extremum does the other path represent?

i) Consider the following ODE for a path on the sphere \begin{align*} \dot{\hat{\boldsymbol r}}\!\bigl( \theta(t), \varphi(t) \bigr) = \Bigl( \hat{\boldsymbol q}_1 \times \hat{\boldsymbol q}_2 \Bigr) \times \hat{\boldsymbol r}\!\bigl( \theta(t), \varphi(t) \bigr) \end{align*} where $\hat{\boldsymbol q}_1$ and $\hat{\boldsymbol q}_2$ are two distinct points on the sphere. Show that for the initial condition $\hat{\boldsymbol q}_1$ the trajectory will proceed through $\hat{\boldsymbol q}_2$. How long does it take to arrive at $\hat{\boldsymbol q}_2$? Does the trajectory represent an extremal path on the sphere? Under which conditions would it be a path of minimal length?

Problem 6.24: 1D dynamical systems with pitchfork and saddle-node bifurcations
We consider the dynamical systems \begin{align} \dot x_a(t) = a + x^2(t) \tag{6.7.1} \end{align} We will analyze now how the solutions $x(t)$ change upon varying the parameter $a \in \mathbb R$.

1. With no loss of generality we will assume that $t_0=0$ and $x_0=x(t_0)=1$. Why is this admissible? Hint: 1. How would the solutions differ when one chooses $t_0=1$ rather than $t_0=0$?
   2. Consider the evolution of $x(t)/x_0^2$ with a suitable change of the time unit and the parameter $a$.
2. With no loss of generality we will assume that $a \in \{ -1, 0, 1 \}$. Why is this admissible? Hint: For $a \neq 0$ you may divide the ODE by $\sqrt{a^2} = ( \sqrt{|a|} )^2$.
3. Solve the differential equation by separation of variables and partial fraction decomposition.
4. Plot the solutions $x_a(t)$ for $a=-1$, $a=0$, and $a=1$. What does this plot tell about the solutions for general $t_0$, $x_0$, and $a$?
5. Determine the fixed points of equation 6.7.1 and plot the bifurcation diagram. Can you see how the structure of the bifurcation diagram fits with the explicit solutions obtained in d)?
6. Repeat the analysis for the system

\begin{align*} \dot x(t) = a\: x(t) + x^3(t) \\ \end{align*}

Problem 6.25: The steel-can pendulum

We consider a pendulum that is built from a steel can with two heavy magnets of identical mass $M$ attached inside (see the figure in the margin). When the can is released it starts oscillating. When pushed, it wobbles along a straight path. The angle between the two magnets is denoted as $\alpha$. We choose our coordinates in such a way that it takes angles in $[0, \pi]$. We describe the configuration of the can by the angle $\theta$ that follows how it is rolling, and we choose the origin of $\theta$ such that the magnets are positioned at $\pm\alpha/2$.

a) Assume that the mass of the can may be neglected as compared to that of the magnets. Determine the kinetic energy, $T$, and the potential energy, $V$, of the can. Use the Lagrange formalism to determine the equation of motion for $\theta$.

b Determine the equilibrium position of the can for $\alpha \not\in \{0\,, \pi\}$, and provide a physical argument why they are stable or unstable. Sketch the according motion in phase space.

c) Discuss the case $\alpha = \pi$. How does the can move in this case? Sketch the trajectories in phase space.

d) For $\alpha = 0$ you should find the following equation of motion \begin{align} 0 = 2\ddot \theta \; \bigl( 1 - \cos \theta \bigr) + \dot \theta^2 \sin\theta + 2\,\omega^2 \: \sin\theta \tag{6.7.2} \end{align} How does $\omega$ depend on the radius $R$ of the can, the mass $M$, and the gravitational acceleration $g$?

e) Verify that the EOM for $\alpha = 0$ simplifies considerably upon introducing the variable $x = \cos(\theta/2)$: \begin{align} \ddot x = \frac{ \omega^2 }{2} \; x \end{align} Hint: 1. Evaluate $\ddot x$.
2. Eliminate $\cos\theta$ and $\sin\theta$ by observing that $1-\cos\theta = 2 \sin^2(\theta/2)$ and $\sin\theta = 2 \sin(\theta/2) \cos(\theta/2)$.
3. Rewrite the remaining expression in terms of $x$.

f)Determine the solution of Equation 6.7.3 for the initial condition as shown in the picture where the steel can is released at rest with some displacement $\theta_0$.

g) \dbend\ Determine the solution of Equation 6.7.3 when the steel can is started at $\theta_0=\pi/2$ with an initial angular speed $-\Omega$. Sketch the phase-space plot for the case $\alpha=0$.