This is an old revision of the document!

2.3 Groups

A group $G$ refers to a set of operations $t\in G$ that are changing some data or objects. Elementary examples refer to reflections in space, turning some sides of a Rubik's cube, or translations in space, as illustrated in \cref{figure:middlePage}. The subsequent action of two group elements $t_1$ and $t_2$ of $G$ is another (typically more complicated) transformation $t_3 \in G$. Analogous to the concatenation of functions, we write $t_3 = t_2 \circ t_1$, and we say $t_3$ is $t_2$ after $t_1$. The set of transformations forms a group iff it obeys the following rules.

Definition 2.6 Group
A set $(G, \circ)$ is called a group with operation $\circ: G \times G \to G$ when the following rules apply

a) The set is closed: $\quad \forall g_1, g_2 \in G : g_1 \circ g_2 \in G$.
b) The set has a neutral element: $\quad \exists e \in G \; \forall g \in G: e \circ g = g$.
c) Each element has an inverse element: $\quad \forall g \in G \; \exists i \in G : g \circ i = e$.
d) The operation $\circ$ is associative: $\quad \forall g_1, g_2, g_3 \in G : ( g_1 \circ g_2 ) \circ g_3 = g_1 \circ ( g_2 \circ g_3 )$.

Definition 2.7 Commutative Group
A group $(G, \circ)$ is called a commutative group when

e) the group operation is commutative: $\forall g_1, g_2 \in G : g_1 \circ g_2 = g_2 \circ g_1$.

Remark 2.5. Commutative groups are also denoted as Abelian groups.

When the group has a finite number of elements the result of the group operation can explicitly be specified by a group table. We demonstrate this by the smallest groups. The empty set can not be a group because it has no neutral element. Therefore the smallest groups have a single element and two elements. Both of these groups are commutative.

Example 2.8 Smallest groups

$(\{ n \}, \odot)$ comprises only the neutral element.

$\odot$	$n$
$n$	$n$

The smallest non-trivial group has two elements $(\{ 0, 1\}, \oplus)$ with

$\oplus$	$0$	$1$
$0$	$0$	$1$
$1$	$1$	$0$

It describes the turning of a piece of paper:
Not turning, $0$, does not change anything (neutral element).
Turning, $1$, shows the other side, and turning twice is equivalent to not turning at all ($1$ is its own inverse).

Remark 2.6. The group properties imply that all elements of the group must appear exactly once in each row and each column of the group table. As a consequence the smallest non-commutative group is the dihedral group of order 6 with six elements that is discussed in \cref{quest:groupSelftest-DihedralD6}.

Rotation of a book by multiples of $\pi/2$ around three orthogonal axes. \label{fig:BuchDrehen}

Example 2.9 Non-commutative groups: rotations
The rotation of an object in space is a group. In particular this holds for the $90^\circ$-rotations of an object around a vertical and a horizontal axis. \cref{fig:BuchDrehen} illustrates that these rotations do not commute.

Remark 2.7. Notations and additional properties:
- Depending of the context the inverse element is denoted as $g^{-1}$ or as $-g$. This depends on whether the operation is considered a multiplication or rather an addition. In accordance with this choice the neutral element is denoted as $1$ or $0$. - The second property of groups, b) $\exists e \in G \; \forall g \in G: e \circ g = g$, implies that also $g \circ e = g$. The proof is provided as \cref{quest:groupSelftest-UniqueNeutralElt}. - When a group is not commutative then one must distinguish the left and right inverse. The condition $g \circ i = e$ does not imply $i \circ g = e$. However, there always is another element $j \in G$ such that $j \circ g = e$. An example is provided in \cref{quest:groupSelftest-DihedralD6}.

2.3.3 Self Test

Problem 2.4: \label{quest:groupSelftest-01} Checking group axioms

Which of the following sets are groups?

a) $\quad ( \mathbb{N}, + )$
b) $\quad ( \mathbb{Z}, + )$

c) $\quad ( \mathbb{Z}, \cdot )$
d) $\quad ( \{+1, -1\}, \cdot )$

$\quad$e) $\quad ( \{ 0 \}, + )$
∗ f) $\quad ( \{ 1, \dots, 12 \}, \oplus )$

where $\oplus$ in f) refers to adding as we do it on a clock,
e.g. $10 \oplus 4 = 2$.

Problem 2.5: \label{quest:groupSelftest-02} The group with three elements

Let $(\mathcal G, \circ)$ be a group with three elements $\{n,l,r\}$, where $n$ is the neutral element.

Show that there only is a single choice for the result of the group operations $a \circ b$ with $a,b \in \mathcal G$.
Provide the group table.
Verify that the group describes the rotations of an equilateral triangle that interchange the positions of the angles.
Show that there is a bijective map $\mathrm{m}:\{n,l,r\} \to \{0,1,2\}$ with the following property:

\begin{align*} \forall a,b \in \mathcal G \: : \: a \circ b = \bigl( \mathrm{m}(a) + \mathrm{m}(b) \bigr) \mathrm{mod} 3 \, . \end{align*} We say that the group $\mathcal G$ is isomorphic to the natural numbers with addition addition modulo 3.¹⁾

Problem 2.6: \label{quest:groupSelftest-03} Symmetry group of rectangles

A polygon has a symmetry with an associated symmetry operation $a$ when $a$ only interchanges the vertices of the polygon. It does not alter the position. To get a grip on this concept we consider the symmetry operations of a rectangle.

Sketch how reflections with respect to a symmetry axis interchange the vertices of a rectangle. What happens when the reflections are repeatedly applied?
Show that the symmetry operations form a group with four elements. Provide a geometric interpretation for all group elements.
Provide the group table.

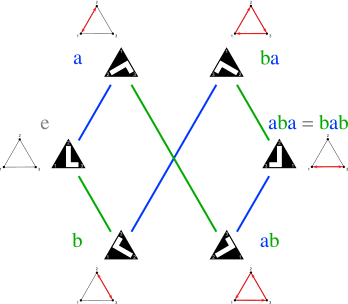
Watchduck (a.k.a. Tilman Piesk), wikimedia CC BY-SA

Reflections of equilateral triangle with respect to the three symmetry axes form a group with six elements; see \cref{quest:groupSelftest-DihedralD6}. \label{fig:DihedralD6}

Problem 2.7: \label{quest:groupSelftest-DihedralD6} Dihedral group of order $6$
\cref{fig:DihedralD6} illustrates the effect of reflections of a triangle with respect to its three symmetry axis. All group elements can be generated by repeated action of two reflections, e.g. those denoted as $a$ and $b$ in the figure.

Verify that the group properties, \Defi{Group}, together with the three additional requirements
$\quad a \circ a = b \circ b = e \quad $ and $\quad a \circ b \circ a = b \circ a \circ b$
imply that the group has exactly six elements,
$\quad \mathcal G = \{ e, a, b, a\circ b, b\circ a, a\circ b\circ a \} \,$.
Work out the group table.
Verify by inspection that $e$ is the neutral element for operation from the right and from the left.
Verify that the group is not commutative, and provide an example of a group element where the left inverse and the right inverse differ.
The group can also be represented in terms of a reflection and the rotations described in \cref{quest:groupSelftest-02}. How would the graphical representation, analogous to \cref{fig:DihedralD6}, look like in that case.

Problem 2.8: \label{quest:groupSelftest-UniqueNeutralElt} Uniqueness of the neutral element
Proof that the group axioms, \Defi{Group}, imply that $e \circ g = g$ implies that also $g \circ e = g$.

¹⁾

The natural number modulo $n$ amount to $n$ classes that represent the remainder of the numbers after division by $n$. For instance, for the natural numbers modulo two the $0$ represents even numbers, and the $1$ odd numbers. Similarly, for the natural numbers modulo three the $0$ represents numbers that are divisible by three, and for the sum of $2$ and $2$ modulo $3$ one obtains $(2+2)\mathrm{mod} 3 = 4\mathrm{mod} 3 = 1$.