Publications
Preprints of my work are available at arXiv
and ResearchGate.
The full list of references is provided by
Orchid
and ResearcherID.
Recent Highlights
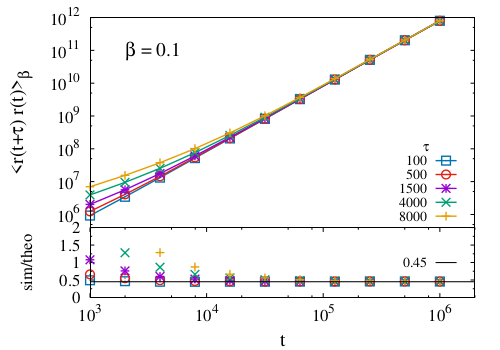
Position Autocorrelation Functions for Anomalous Transport
C. Giberti, L. Rondoni, M. Tayyab, J. Vollmer
We introduce an exactly solvable model featuring anomalous transport, the slicer map (SM). The moments of displacement of the model can be mapped to those of hightly non-trivial 1d transport model with quenched disorder, the Lévy-Lorentz gas (LLg) by matching the exponent for the mean-square displacement. Once this is done also the exact solution of the position-position autocorrelation function of the SM provides a faithful description of the correlations observed in numerical solutions of the LLg.
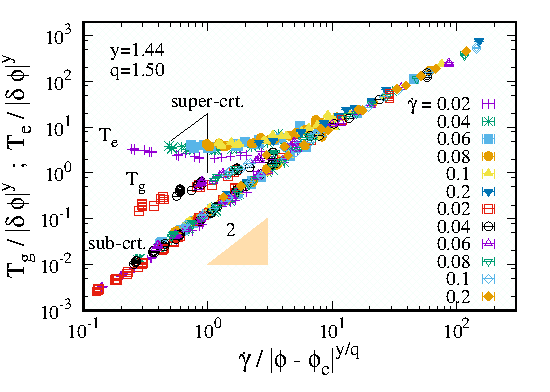
Temperatures of Dense Particulate Flows
S.H.E. Rahbari, A.A. Saberi, H. Park, J. Vollmer
Soft particulate materials comprise dense arrangements of entities, like bubbles or grains, that dissipate energy upon interaction. The description of their flow is a test case for the thermodynamics of far-from-equilibrium materials. We show that rare flucutations of the flows obey a fluctuation theorem, and that it can be used to define a temperature Te of the fluid. In the low density regime it agrees with the kinetic temperature Tg. In the yield-stress regime, where Te is not expected to be a sound physical observable, they differ.
Nature Communications 8 (2017) 11 » press release » arXiv:1702.07137 »
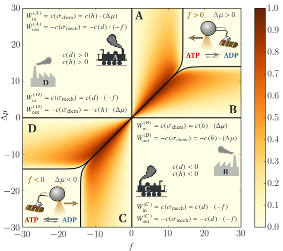
Fluctuating Currents
in Stochastic Thermodynamics
B. Altaner, A. Wachtel, J. Vollmer
Stochastic thermodynamics uses Markovian jump processes to model random transitions between observable mesoscopic states. Physical currents are obtained from antisymmetric jump observables defined on the edges of the graph representing the network of states. The asymptotic statistics of such currents are characterized by scaled cumulants. In the present work, we use the algebraic and topological structure of Markovian models to prove a gauge invariance of the scaled cumulant-generating function. Exploiting this invariance yields an efficient algorithm for practical calculations of asymptotic averages and correlation integrals.
Physical Review E 92 (2015) 042132 »
Physical Review E 92 (2015) 042133 »
arXiv:1407.2065 »
arXiv:1504.03648 »
Archive
Laura Stricker, Jürgen Vollmer
Physical Review E 92 (2015) 042406
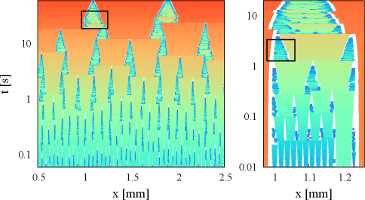
Impact of microphysics on the growth of one-dimensional breath figures
PRE »
arXiv:1502.00566 »
Droplet patterns condensing on solid substrates (breath figures) tend to evolve into a self-similar regime, characterized by a bimodal droplet size distribution. The size distribution of the smaller droplets follows a scaling law characterized by a nontrivial polydispersity exponent. We present a numerical model for three-dimensional droplets on a one-dimensional substrate (fiber) that accounts for droplet nucleation, growth, and merging. The polydispersity exponent retrieved using this model is not universal. Rather it depends on the microscopic details of droplet nucleation and merging.
C. Marschler, J. Vollmer
SIAM J. Appl. Dyn. Systems 13 (2014) 1137–115
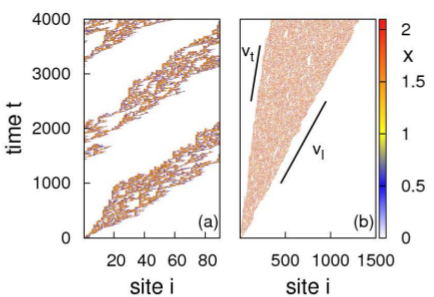
Unidirectionally Coupled Map Lattices with Nonlinear Coupling: Unbinding Transitions and Superlong Transients
SIAM J Appl Dyn Syst »
arXiv:1405.1911 »
We introduce a unidirectionally coupled map lattice that mimics three of the salient features of pipe-flow turbulence: (i) the transition from laminar flow to puffs, (ii) a superexponential scaling of puff lifetime, and (iii) the transition from puffs to slugs by an unbinding transition in an intermittency scenario. In our model all transitions and scalings are theoretically described from a dynamical systems point of view.
Jürgen Vollmer, Ariane Papke, Martin Rohloff
Frontiers in Physics 2 (2014) 18
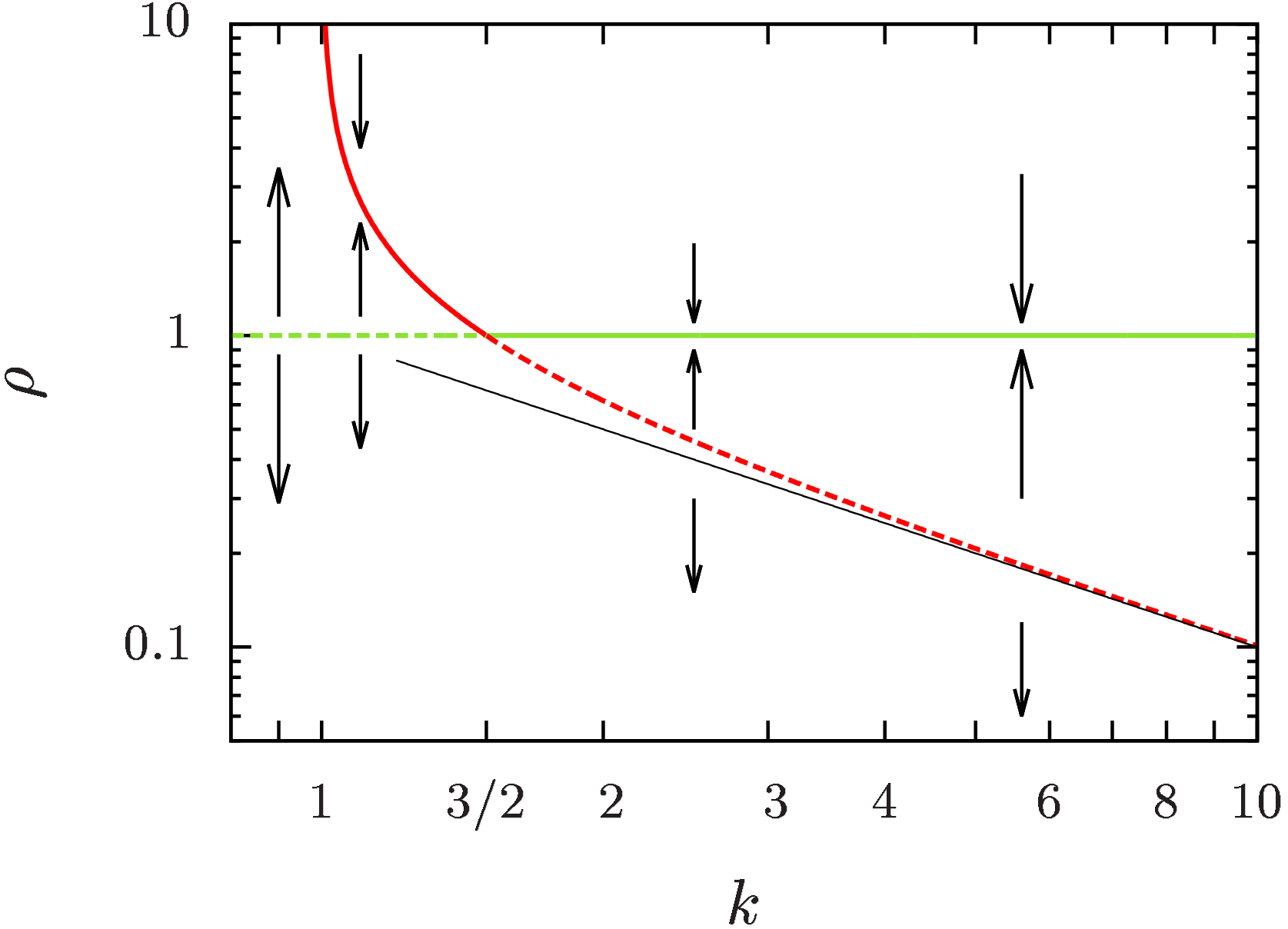
Ripening and focusing of aggregate size distributions with overall volume growth
Frontiers »
arXiv:1403.2661 »
We explore the evolution of the aggregate size distribution in systems where aggregates grow by diffusive accretion of mass. Supersaturation is controlled in such a way that the overall aggregate volume grows linearly in time. Classical Ostwald ripening, which is recovered in the limit of vanishing overall growth, constitutes an unstable solution of the dynamics. In the presence of overall growth the evaporation of aggregates always drives the dynamics into a new, qualitatively different growth regime where ripening ceases, and growth proceeds at a constant number density of aggregates. We provide a comprehensive description of the evolution of the aggregate size distribution in this constant density regime: the size distribution does not approach a universal shape, and even for moderate overall growth rates the standard deviation of the aggregate radius decays monotonically. The implications of this theory for the focusing of aggregate size distributions are discussed for a range of different settings including the growth of tiny rain droplets in clouds, as long as they do not yet feel gravity, and the synthesis of nano-particles and quantum dots.
Johannes Blaschke, Tobias Lapp, Björn Hof, Jürgen Vollmer
Physical Review Letters 109 (2012) 068701
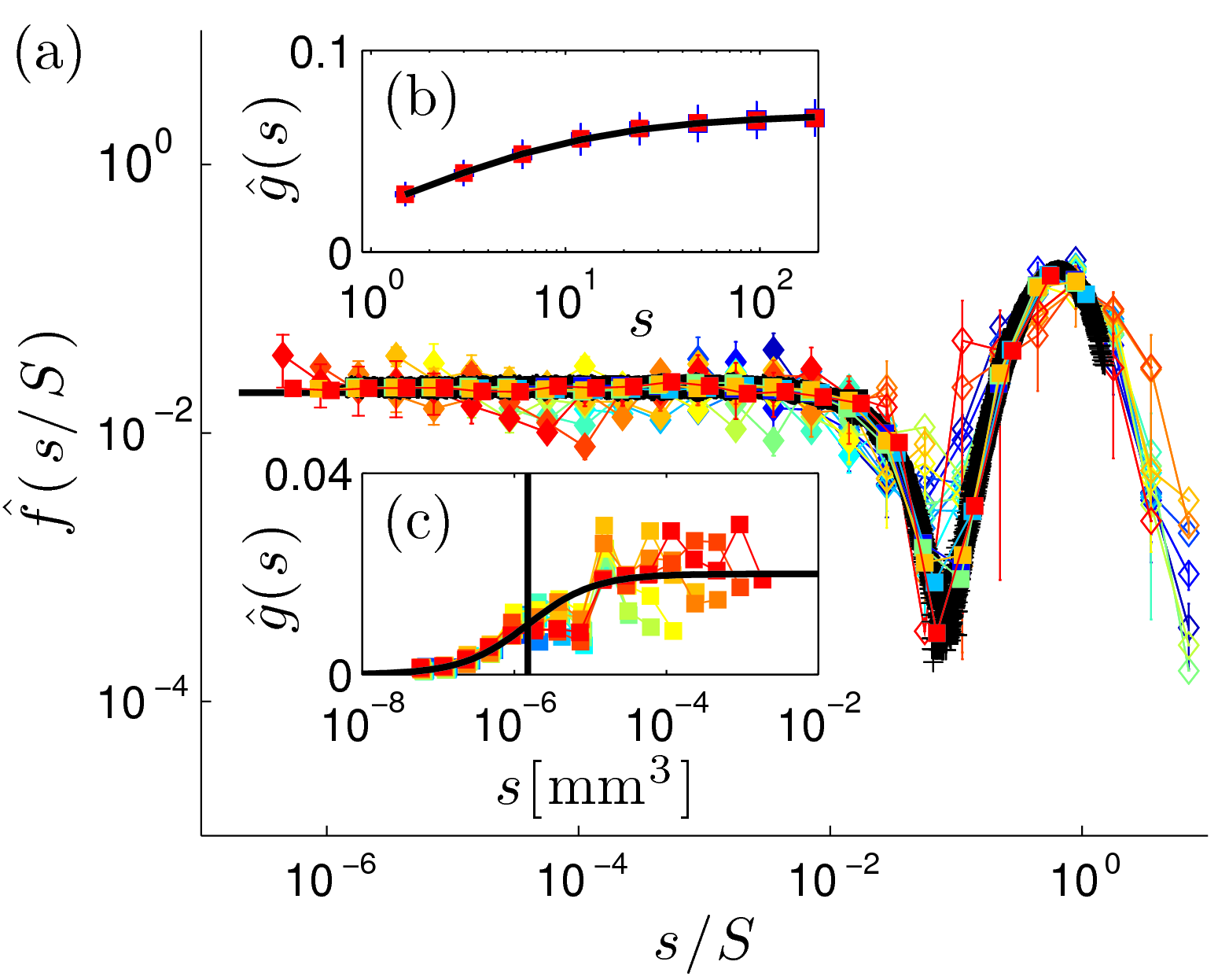
Breath Figures: Nucleation, Growth, Coalescence, and the Size Distribution of Droplets
PRL »
arXiv:1206.6705 »
press release »
The analysis of the size distribution of droplets condensing on a substrate (breath figures) is a test ground for scaling theories. Here, we show that a faithful description of these distributions must explicitly deal with the growth mechanisms of the droplets. This finding establishes a gateway connecting nucleation and growth of the smallest droplets on surfaces to gross features of the evolution of the droplet size distribution.
Bernhard Altaner, Jürgen Vollmer
Physical Review Letters 108 (2012) 228101
Fluctuation-Preserving Coarse Graining for Biochemical Systems
PRL »
arXiv:1112.4745 »
Finite stochastic Markov models play a major role in modeling biological systems. Such models are a coarse-grained description of the underlying microscopic dynamics and can be considered mesoscopic. The level of coarse-graining is to a certain extent arbitrary since it depends on the resolution of accommodating measurements. Here we present a systematic way to simplify such stochastic descriptions which preserves both the meso-micro and the meso-macro connections. The former is achieved by demanding locality, the latter by considering cycles on the network of states. Our method preserves fluctuations of observables much better than naı̈ve approaches.
Tobias Schneider, Bruno Eckhardt, Jürgen Vollmer,
Physical Review E 75 (2007) 066313
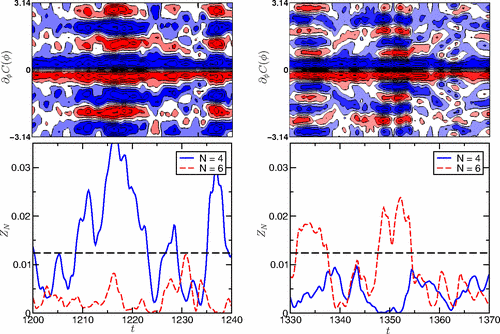
Statistical analysis of coherent structures in transitional pipe flow
PRE »
arXiv:physics/0611020 »
Numerical and experimental studies of transitional pipe flow have shown the prevalence of coherent flow structures that are dominated by downstream vortices. They attract special attention because they contribute predominantly to the increase of the Reynolds stresses in turbulent flow. In the present study we introduce a convenient detector for these coherent states, calculate the fraction of time the structures appear in the flow, and present a Markov model for the transition between the structures. The fraction of states that show vortical structures exceeds 24% for a Reynolds number of about Re=2200, and it decreases to about 20% for Re=2500. The Markov model for the transition between these states is in good agreement with the observed fraction of states, and in reasonable agreement with the prediction for their persistence. It provides insight into dominant qualitative changes of the flow when increasing the Reynolds number.