Modeling Transport Processes
We strive for a fundamental understanding of transport processes by analyzing classes of representative model systems. In particular, this is interesting to us when it involves model hierarchies where complex behaviour emerges on macroscopic scales (self-organization). We aim at developing archetypical models that can be treated analytically. The resulting predictions are compared with experimental findings and numerical simulations (cf. Physics). This comparison involves dedicated algorithms for data and image processing.
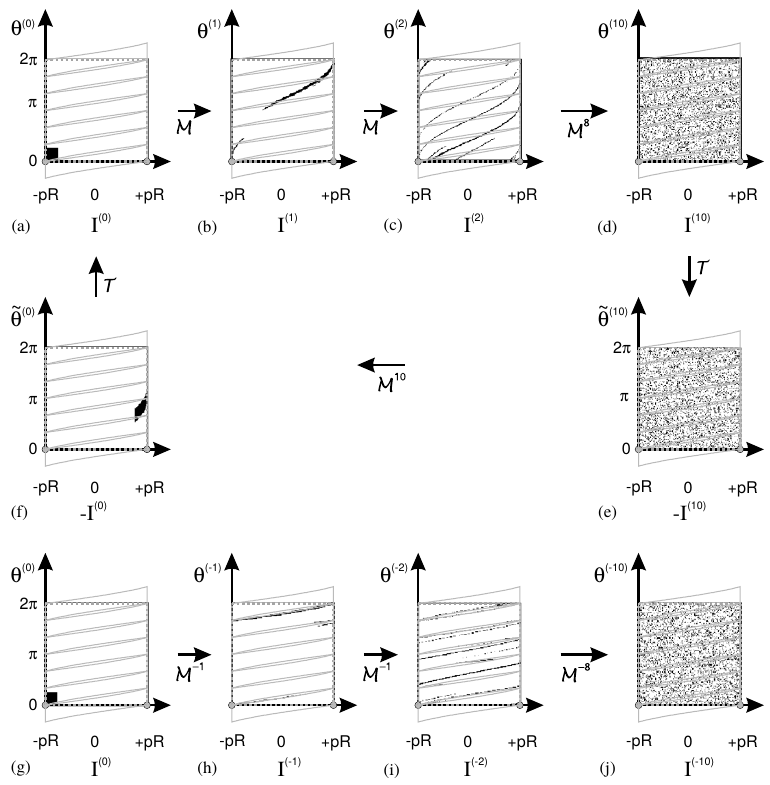
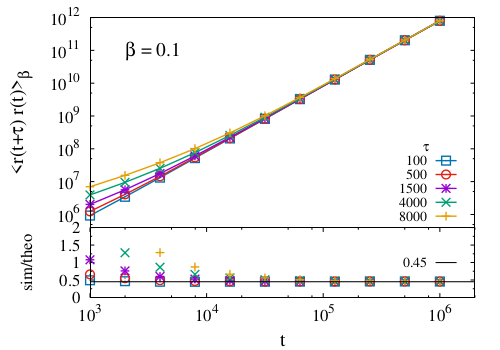
Anomalous Transport. Calculating Position Auto-Correlation Functions.
A transport process is denoted anomalous when nth moment of the displacement is not scaling like the power n/2 of time. There is a considerable volume of theoretical work addressing such an anomalous scaling of the moments. However, little is known about position correlation functions. We introduce an exactly solvable model featuring anomalous transport, the slicer map (SM). By matching its exponent for the mean-square displacement the moments of displacement of the SM are mapped to those of a hightly non-trivial system with quenched disorder, the Lévy-Lorentz gas (LLg). This matching also provides a faithful description of the correlations observed in numerical solutions of the LLg.
with Lamberto Rondoni, Claudio Giberti, Mohammad Tayyab
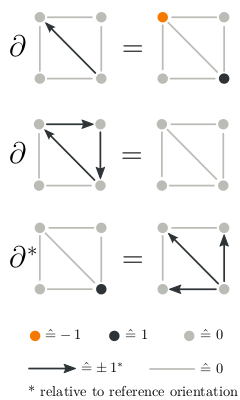
Stochastic Thermodynamics. Calculating Cumulants of Distribution Functions.
Stochastic thermodynamics uses Markovian jump processes to model random transitions between observable mesoscopic states. Physical currents are obtained from antisymmetric jump observables defined on the edges of the graph representing the network of states. The asymptotic statistics of such currents are characterized by scaled cumulants. In the present work, we use the algebraic and topological structure of Markovian models to prove a gauge invariance of the scaled cumulant-generating function.
with Artur Wachtel, Bernhard Altaner
Physical Review E 92 (2015) 042132 » Physical Review E 92 (2015) 042133 »
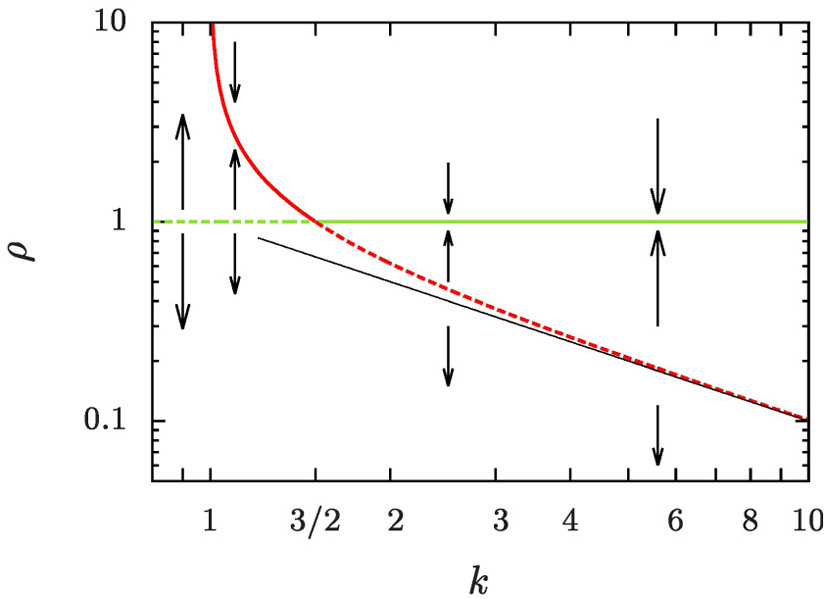
Ripening. Crossing from Scaling to Size Focusing.
We explore the evolution of the aggregate size distribution in systems where aggregates grow by diffusive accretion of mass. Supersaturation is controlled in such a way that the overall aggregate volume grows linearly in time. Classical Ostwald ripening is recovered in the limit of vanishing overall growth. We show that the associated scaling solution constitutes an unstable solution of the dynamics. In the presence of overall growth the dynamics approaches a new, qualitatively different growth regime that features size focusing at a fixed droplet density.
with Martin Rohloff
Coherent Structures and Super-Long Transients in Dynamical Systems Models.
We developed algorithms to detect coherent structures in pipe flow, and characterize their role as a scaffold for an emerging turbulent dynamics. Subsequently, dynamical-systems models were developed that model the transition from transient to permament turbulent behaviour and the associated anomalous scaling.
with Bruno Eckhardt, Tobias Schneider, Christian Marschler
SIAM J. Appl. Dyn. Systems 13 (2014) 1137–115 » New J. Phys. 11 (2009) 013040 » Phys. Rev. E 75 (2007) 066313 »
Multibaker Maps. Microscopic Dynamics and Transport Equations.
Ergodic Theory involves the derivation of the formalism of Equilibrium Statistical Physics and its relation to Thermodynamics from reversible microscipic equations of motion. We have developed Multibaker Maps as a formal generalization of this model hierarchy to address the derivation of transport equations in systems that obey detailed balance.
with Tamas Tel, Wolfgang Breymann, Laszlo Matyas, Lamberto Rondoni
Physics Reports 372 (2002) 131 » Phys. Rev. E 61 (2000) R4679 » Phys. Rev. Lett. 79 (1997) 2759 » Phys. Rev. Lett. 77 (1996) 2945 »