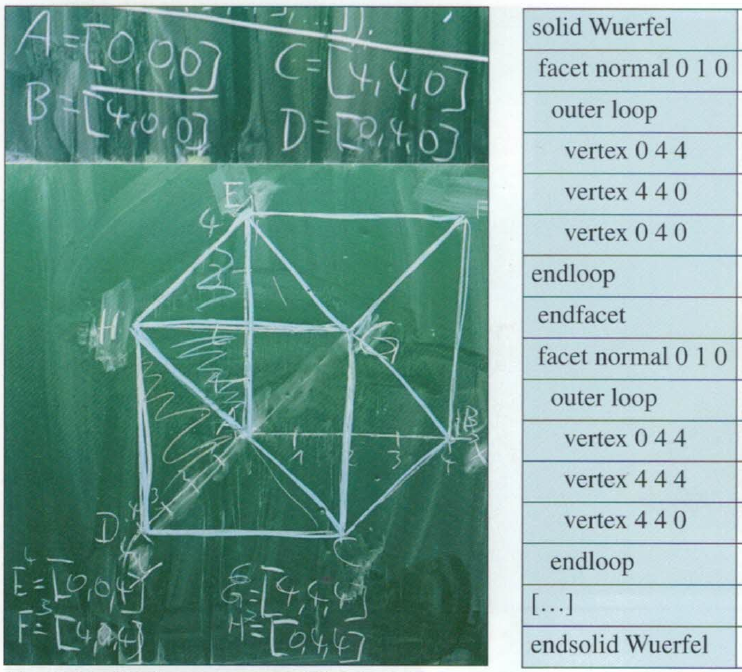
Maths teaching and 3D printing.
3d printing offers a wealth of new opportunities for teaching mathematics.

Digitizing Models.
We digitize the Göttingen Collection of Mathematical Models and Instruments to make it available again for class room teaching. Part of this work is done in the form of research seminars.
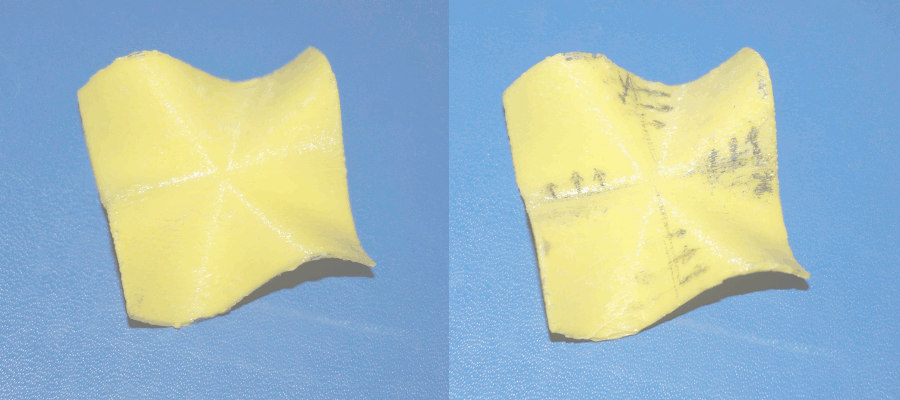
Designing Models and Instruments.
Simple models can be constructed from scratch. More complex models can be constructed in blender, or via straight-forward Python programs.