Table of Contents
4.10 Problems
4.10.1 Rehearsing Concepts
Problem 4.23:
Maximum distance of flight
There is a well-known rule that one should through a ball at an angle of roughly $\theta = \pi/4$
to achieve a maximum width.
- Solve the equation of motion of the ball thrown in $x$ direction with another velocity component in vertical $z$ direction. Do not consider friction in this discussion, and verify that the ball will then proceeds on a parabolic trajectory in the $(x,z)$ plane.
- Well-trained shot put pushers push the put with an initial angle substantially smaller than $\pi/4$, i.e., they provide more forward than upward thrust. Verify that this is a good idea when the height $H$ of the release point of the trajectory over the ground is noticeable as compared to the length $L$ between the release point and touchdown, i.e. when $H/L$ is not small.
What is the optimum choice of $\theta$ for the shot put?
- Consider now friction: Is it relevant for the conclusions on throwing shot puts? Is it relevant for throwing a ball? How much does it impact the maximum distance that one can reach in a gun shot?
Problem 4.24:
Phase-space portraits for a scattering problem
- Sketch the potential $\Phi(x) = 1-1/\cosh x$ for $x \in \mathbb{R}$.
- Sketch the direction field in the phase space for the EOM $\ddot x = -\partial_x\Phi(x)$.
- Show that $E = \frac{1}{2} \, \dot x^2 + \Phi(x)$ is a constant of motion of the EOM.
- Use energy conservation to determine the shape of the trajectories in phase space, and add a few trajectories to the plot started in b).
Add to the sketch a the phase portrait of the motion in this potential, i.e., the solutions of in the phase space $(x, \dot x)$.
Problem 4.25:
Another linear ODEs with constant coefficients
Consider the ODE
\begin{align*}
\ddot x = a \, x
\qquad \text{ with } a \in \mathbb{R}_+
\end{align*}
- Sketch the direction field in phase space.
- Find the solutions of $x(x)$.
- Add the trajectories the are proceeding through the points $(x(t_0), \dot x(t_0)) \in \{ (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1), (1,-1) \}$ to the plot started in a). Hint:
Problem 4.26:
Stokes drag
The EOM for Stokes friction, Equation 4.3.1 is a linear differential equation.
Adopt the strategy for solving linear differential equations, Algorithm 4.3,
to find the solution Equation 4.3.3 b.
4.10.2 Practicing Concepts
Problem 4.27: Egyptian water clocks
In ancient Egypt time was measured by following how water is running out of a
container with a constant cross section $A$.
At a water level $h$ in the container,
the water will then run out at a speed
\begin{align*}
v(t) = -c \; \sqrt{2 g \, h(t)}
\end{align*}
where the numerical constant $c$ accounts for the viscosity of water
and the geometry of the vessel.
The Egyptian water clocks this constant takes values of the order of $c \simeq 0.6$.
- How does the height $h(t)$ of the water in he container evolve after the plug is pulled?
For use as a clock it would be desirable to change the design of the clock such that $h(t)$ would decrease linearly in time. How can the construction of the water clock be amended to reach that aim?
Problem 4.28:
Damped oscillator
Physical systems are subjected to friction.
This can be taken into account by augmenting the EOM of a particle suspended from a spring, Equation 4.5.1, by a friction term
\begin{align*}
m \, \ddot z(t) = -m \, g - k \, z(t) - \mu \, \dot z(t)
\end{align*}
a) How does friction affect the motion $z(t)$ of the particle? What is the condition that there are still oscillations, even though with a damping? For which parameters will they disappear, and how do the solutions look like in that case?
b) Sketch the evolution of the trajectories in phase space, for the two settings with and without oscillations.
c) For the borderline case the characteristic polynomial will only have a single root, $\lambda$. Verify that the general solution can then be written as \begin{align*} z(t) = z_0 + A_1 \, \mathrm{e}^{\lambda \, (t-t_0)} + A_2 \, t \, \mathrm{e}^{\lambda \, (t-t_0)} \end{align*}
d) Determine the solutions for a particle for the following initial conditions:
- the particle is at rest and at a distance $A$ from its equilibrium position,
- the particle is at the equilibrium position, but it has an initial velocity $v_0$.
Indicate the form of these trajectories in the phase-space plots.
Problem 4.29:
One-dimensional collisions in the center-of-mass frame
In Example 3.12 we discussed one-dimensional collisions for settings where the second particle is initially at rest.
Now, we consider the situation where both particles are moving from the beginning.
Specifically, we consider a setting with two particles of masses $m_1$ and $m_2$
with the initial conditions $\bigl( q_1(t_0), v_1 \bigr)$ and $\bigl( q_2(t_0), v_2 \bigr)$.
a) Show that the center of mass
$Q(t) = \bigl( m_1 \, x_1(t) + m_2 \, x_2(t) \bigr)/M$ with $M=m_1+m_2$
of the two particles evolves as
\begin{align*}
Q(t) = Q(t_0) + \dot Q(t_0) \: ( t - t_0 )
\quad\text{ where }\quad
\dot Q(t_0) = a_1 \, v_1 + a_2 \, v_2
\end{align*}
and determine the associated real constants $a_1$ and $a_2$.
b) We denote the relative coordinates as $x_i = q_i - Q$
and associate it with a momentum $m_i \, \dot x_i$.
Show that the relative momenta add up to zero before and after the collision,
\begin{align*}
0 = m_1 \, x_1 + m_2 \, x_2
= m_1 \, \bigl( q_1 - Q \bigr) + m_2 \, \bigl( q_2 - Q \bigr)
\end{align*}
and that they swap signs upon collision. Hint:
c) Determine the time evolution before and after the collision.
d) Verify the consistency of your result with the special case treated in Example 3.12.
Problem 4.30:
Motion in a harmonic central force field
A particle of mass $m$ and at position $\mathbf r(t)$ is moving under the influence of a central force field
\begin{align*}
\mathbf F( \mathbf r ) = - k \, \mathbf r \, .
\end{align*}
- We want to use the force to build a particle trap1), i.e. to make sure that the particle trajectories $\mathbf r(t)$ are bounded: For all initial conditions there is a bound $B$ such that $| \mathbf r(t) | < B$ for all times $t$. What is the requirement on $k$ to achieve this aim?
- Determine the energy of the particle and show that the energy is conserved.
- Demonstrate that the angular momentum $\mathbf L = \mathbf r \times m\,\dot{\mathbf r}$ of the particle is conserved, too. Is this also true when considering a different origin of the coordinate system? Hint:
- Let $(x_1, x_2)$ be the coordinates in the plane that is singled out by the angular momentum conservation. Show that $m \ddot x_i(t) + k\,x_i(t) = 0$ for $i\in\{1,2\}$. Determine the solution of these equations. Sketch the trajectories in the phase space $(x_i, \dot x_i)$. What determines the shape of the trajectories?
- Show that the trajectories in the configuration space $(x_1, x_2)$ are ellipses. What determines the shape of these trajectories?
- Discuss the relation between the amplitude and shape of the trajectory, as determined by the ratio and the geometric mean of the major axes of the ellipse in configuration space, and the period of the trajectory.
4.10.3 Mathematical Foundation
Problem 4.31: Differential equations and functional dependencies
Determine ODEs whose general solutions are of the form
- $y(x) = C \, x^2 -x$
- $y^2(x) = A \, x + B$
Here, $A$, $B$, and $C$ are real constants that will be determined by the IC of the ODE.
Problem 4.32:
Separation of variables for a non-autonomous ODE
We consider the ODE
\begin{align*}
y'(x) = \frac{x}{y}
\end{align*}
a) How many degrees of freedom does this system have? What is its space? State it as a first order ODE in terms of the phase-space variables.
b) Sketch the direction field in phase space.
c) Find the solution of the ODE for ICs $(x_0, y_0)$ with $y_0 \neq 0$ and
- $x_0 < 0$ and $x_0 < y_0 < -x_0$
- $x_0 > 0$ and $x_0 > y_0 > -x_0$
- other ICs with $\lvert x_0 \rvert \neq \lvert y_0 \rvert$
- $\lvert x_0 \rvert = \lvert y_0 \rvert$
d) Determine the largest interval of values $x \in \mathbb{R}$ where the solutions $y(x)$ obtained in b) are defined.
e) Is the function $y(x) = \lvert x \rvert$ a solution of the ODE?
If in doubt: Where do you see problems for this solution?
Problem 4.33: Effective potentials and phase-space portraits
We consider ODEs of the form
\begin{align*}
\ddot x(t) = - \frac{ \mathrm{d} }{\mathrm{d} x} V_{\text{eff}}(x)
\end{align*}
Sketch the solutions for trajectories in the following potentials
in the phase space$(x, \dot x)$.
\begin{align*}
\begin{array}{llll}
\text{a)}\quad
& V_{\text{eff}} = x \, \sin x
& \qquad\qquad\qquad \text{b)}\quad
& V_{\text{eff}} = x \, \cos x
\\
\text{c)}\quad
& V_{\text{eff}} = x - \sin x
& \qquad\qquad\qquad \text{d)}\quad
& V_{\text{eff}} = x - \cos x
\\
\text{e)}\quad
& V_{\text{eff}} = \mathrm{e}^x \, \sin x
& \qquad\qquad\qquad \text{f)}\quad
& V_{\text{eff}} = \mathrm{e}^{-x} \, \sin x
\end{array}
\end{align*}
Problem 4.34:
Central forces conserve angular momentum
Consider a system of $N$ particles at the positions $\mathbf q_i$ with masses $m_i$
where each pair $(ij)$ interacts by a force
$\mathbf F_{ij}( | \mathbf d_{ij} | )$
acting parallel to the displacement vector $\mathbf d_{ij} = \mathbf q_j - \mathbf q_i$ from particle $i$ to $j$.
Proof the following statements:
a) The evolution of the center of mass of the system
\begin{align*}
\mathbf Q = \frac{1}{M} \: \sum_{i=0}^N m_i \mathbf q_i
\quad\text{ with }\quad
M = \sum_{i=0}^N m_i
\end{align*}
is force free, i.e., $\ddot{\mathbf Q} = \mathbf 0$.
b) The total angular momentum can be written as
\begin{align*}
\mathbf L_{\text{tot}}
= M \, \mathbf Q \times \dot{\mathbf Q}
+ \sum_{i<j} \mu_{ij} \; \mathbf d_{ij} \times \dot{\mathbf d}_{ij}
\end{align*}
Determine the factors $\mu_{ij}$.
c) The two contributions to the angular momentum,
$M \, \mathbf Q \times \dot{\mathbf Q}$ and the sum
$\sum_{i<j} \mu_{ij} \; \mathbf d_{ij} \times \dot{\mathbf d}_{ij}$
are both conserved.
Problem 4.35:
Impact of translations on conservation laws
We consider a coordinate transformation where the origin of the coordinate systems is moved to a new time-dependent position $\mathbf x(t)$,
\begin{align*}
\mathbf q_i(t) = \mathbf x(t) + \mathbf r_i(t)
\end{align*}
a) Show that the expressions for the kinetic energy are related by
\begin{align*}
T = \sum_i \frac{m_i}{2} \: \dot{\mathbf q}_i^2
= \frac{M}{2} \; \dot{\mathbf x}^2
+ M \: \dot{\mathbf x} \cdot \dot{\mathbf Q}
+ \sum_i \frac{m_i}{2} \: \dot{\mathbf r}_i^2
\end{align*}
Here, $M = \sum_i m_i$ and $\mathbf Q = M^{-1} \: \sum_i m_i \mathbf q_i$
are the total mass and the center of mass, respectively.
b) Show that the expressions for the total energy for motion in an external field
are related by
\begin{align*}
E = T - M \, \mathbf g \cdot \mathbf Q + \sum_{i<j} \Phi_{ij}\bigl( \lvert \mathbf q_i - \mathbf q_j \rvert \bigr)
= T
- M \, \mathbf g \cdot \mathbf Q
+ \sum_{i<j} \Phi_{ij}\bigl( \lvert \mathbf r_i - \mathbf r_j \rvert \bigr)
- M \, \mathbf g \cdot \mathbf x
\end{align*}
c) Show that the angular momentum transforms as follows
\begin{align*}
L
= \sum_i m_i \, \mathbf q_i \times \dot{\mathbf q}_i
= M \, \mathbf x \times \dot{\mathbf Q}
+ M \, \bigl( \mathbf x + \mathbf Q ) \times \dot{\mathbf x}
+ \sum_i m_i \, \mathbf x_i \times \dot{\mathbf x}_i
\end{align*}
d) Show that conservation laws are mapped to conservation laws
iff we consider a Galilei transformation,
i.e., a transformation where $\dot x = $const.
4.10.4 Transfer and Bonus Problems, Riddles
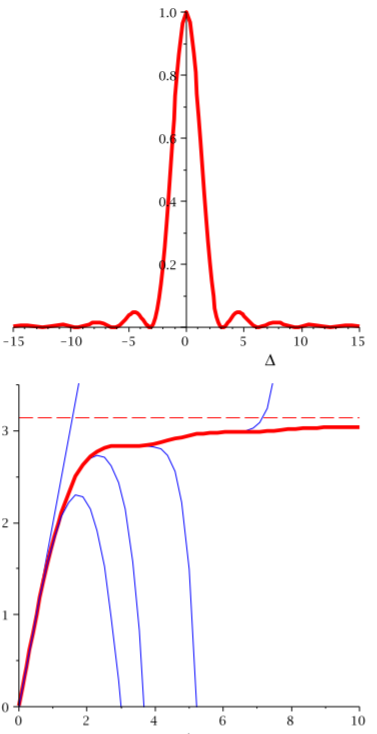
Figure 4.20: The upper panel shows the light intensity
$I( x )/I_{\text{max}}$,
and the lower panel the fraction of light in the center region of width $\Delta$,
i.e., the power
$P(\Delta) = \left[ \int_{-\Delta}^{\Delta}
I( x ) \text{d}x \right] / I_{\text{max}}$.
The red dotted value marks the asymptotic value $\pi$
and the blue line the approximations obtained by a Taylor approximation
up to order
2, 4, 8, 16, and 32. according to the Taylor series evaluated in
Problem 3.6 b).
Problem 4.36: Light intensity at single-slit diffraction
Monochromatic light of wave length $\lambda$
that is passion through a slit
will produce an
diffraction pattern on a screen
where the intensity follows
(cf. Figure 4.20, top panel)
\begin{align*}
I( x ) = I_{\text{max}} \; \left( \frac{ \sin x }{x} \right)^2
\end{align*}
Here the light intensity $I(x)$ is the power per unit area
that is observed at a distance $x$ to the side
from the direction straight ahead from the light source through the slit to the screen.
We are interested in the total power $P(\Delta)$ that falls into a region of width $\lvert x \rvert < \Delta$.
Since there is no antiderivative for $I(x)$ we will find approximate solutions by
considering Taylor approximations of $I(x)$
that can be integrated without effort.
a) Show that $\sin^2 x = ( 1 - \cos 2x )/2$,
and use the Taylor expansion of the cosine-function to show that
\begin{align*}
\frac{ \sin^2 x }{x^2}
= \frac{ 1 - \cos 2x }{ 2 x^2 }
= 2 \; \sum_{n=0}^{\infty} \; \frac{(-1)^n}{(2n+2)!} \; (2x)^{2n}
\end{align*}
b) Determine the Taylor approximations for $P(\Delta)$
by integrating the expression found in a).
c) Write a program that is numerically determines $P(\Delta)$ and compares it to Taylor approximations of different order, as shown in the lower panel of Figure 4.20.
Problem 4.37:
Tricky issues in a classical population model
The Lotka-Volterra model is considered the first model addressing the evolution of populations in theoretical biology.
It predicts oscillations of populations,
and still today it is cited in the context of data of Lynx and Hare
that were collected in Canada in the late 19th century
(cf. Figure 4.21).
Let
$H(t)$ be the population of prey animals (Hare) and
$L(t)$ be the population of its predator (Lynx).
When there are no predators the population of prey grows exponentially with a rate $a$,
and this rate is reduced by $- b L(t)$,
when prey is consumed by predators.
In absence of food the predators die at a rate $d$,
and this rate is reduced by $-c H(t)$, when they find food.
\begin{align*}
\dot H(t) &= H(t) \; \left[ a - b \, L(t) \right]
\\
\dot L(t) &= L(t) \; \left[ c \, H(t) - d \right]
\end{align*}
a) Let
$u(\tau) \propto H(t)$,
$v(\tau) \propto L(t)$, and
$\tau \propto t$.
Find suitable proportionality constants and a dimensionless parameter $\Pi$ such that
\begin{align*}
\dot u(\tau) &= \quad u(\tau) \; \left[ 1 - v(t) \right]
\\
\dot v(\tau) &= \Pi^2 \; v(\tau) \; \left[ u(\tau) - 1 \right]
\end{align*}
b) Show that the EOM for this biological system has fixed points at $(0,0)$ and $(1,1)$.
How does the population model behave close to these fixed points?
c) Sketch the evolution of the solutions in the $(u,v)$-plane,
and compare your result with the data reported on the lynx and hare
that are shown in Figure 4.21.
Can you find the qualitative difference of the data and behavior predicted by the model? **Hint:**
Who would be eating whom?
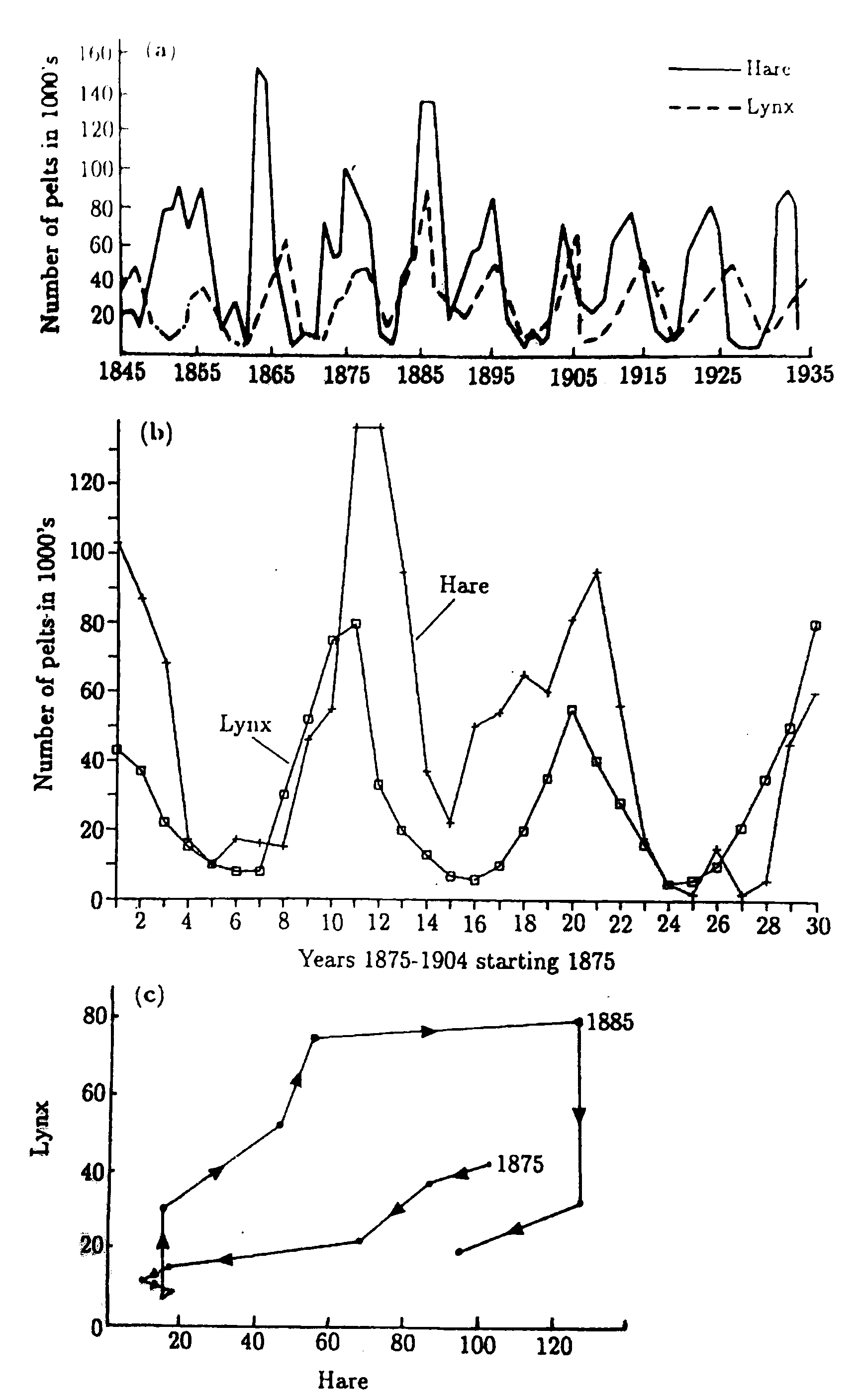 Figure 4.21:
( a) Annual oscillations of the skins of hare and lynx offered to the Hudson Bay company.
( b) Data with higher time resolution for the $30$ years between 1875 and 1904.
( c) Presentation of the data presented in(b) as a phase-space plot.
[reproduced from Fig.3.3. of Murray (2002).
The book provides a thorough discussion of populations models,
their assumptions and artifacts for a range of different populations models.]
Figure 4.21:
( a) Annual oscillations of the skins of hare and lynx offered to the Hudson Bay company.
( b) Data with higher time resolution for the $30$ years between 1875 and 1904.
( c) Presentation of the data presented in(b) as a phase-space plot.
[reproduced from Fig.3.3. of Murray (2002).
The book provides a thorough discussion of populations models,
their assumptions and artifacts for a range of different populations models.]
d) One can infer the form of the trajectories in phase space by observing that
\begin{align*}
\frac{\mathrm{d} v}{\mathrm{d} u} = \frac{\dot v}{\dot u} = \pi^2 \; \frac{v \, (u-1)}{u \, (1-v)} \, .
\end{align*}
Why does this hold?
e) Find the solution of the ODE by separation of variables and
show that the result implies the following constant of motion
\begin{align*}
\Phi( u, v ) = \ln\left( v \, u^{\alpha} \right) - v - \alpha \, u \, ,\\
\qquad\text{with a suitably chosen $\alpha > 0$.}
\end{align*}
Verify this result by also determining the time derivative of $\Phi( u(\tau), v(\tau) )$.
Here $( u(\tau), v(\tau) )$ is a solution of the EOM.
Remark:
The presence of a conservation law should be considered an artifact of the model
whenever there is no model-immanent (i.e., required by the biological problem in this cases) reason for it to exist.