Table of Contents
3.4 Constants of motion (CM)
In the previous section we saw that Newton's laws can be expressed as equations relating the second derivative of the position of a particle to the forces acting on the particle. The forces are determined as part of setting up the physical model. Subsequently, determining the time dependence of the position is a mathematical problem. Often it can be solved by finding constraints on the solution that must hold for all times. Such a constraint is called a
Definition 3.4 Constant of motion
A function $\mathcal{C} (\mathbf q , \dot{\mathbf q} ,t)$ is a constant of motion (CM) iff its time derivative vanishes, \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (\mathbf q , \dot{\mathbf q} ,t) = 0 \end{align*}
It provides us with an opportunity to take a closer look at the expressions that emerge when taking derivatives of functions with arguments that are vectors. In order to evaluate the time derivative of $\mathcal C$ we write $\mathbf q = (q_1 , ....., q_D)$, and apply the chain rule \begin{align} \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (\mathbf q(t) , \dot{\mathbf q}(t) ,t) &= \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (q_1(t), \cdots, q_D(t) , \dot q_1(t), \cdots, \dot q_D(t) ,t) \nonumber \\ &= \sum_{i=1}^{D} \frac{\mathrm{d} q_i}{\mathrm{d} t} \frac{\partial \mathcal C}{\partial q_i} + \sum_{i=1}^{D} \frac{\mathrm{d} \dot q_i}{\mathrm{d} t} \; \frac{\partial \mathcal{C}}{\partial \dot q_i} + \frac{\partial \mathcal{C}}{\partial t} \tag{3.4.1} \end{align} In this expression the operation $\partial$ is called `partial', and the derivative $\partial \mathcal{C} / \partial q_i$ is denoted as partial derivative of $\mathcal C$ with respect to $q_i$. For the purpose of calculating the partial derivative, we consider $\mathcal{C}$ to be a function of only the single argument $q_i$. For sake of a more compact notation we also write $\partial_{q_i} \mathcal{C}$ rather than $\partial \mathcal{C} / \partial q_i$. Moreover, when it is not clear from the context which conditions are adopted, they can explicitly be stated as subscript of a vertical bar to the right of the derivative (or even square brackets).
Example 3.7: Partial derivatives
For $f(x,y) = x/\sqrt{x^2+y^2}$ and $R=\sqrt{x^2+y^2}$ we have \begin{align*} \left. \partial_x f(x,y) \right\rvert_y &= \frac{1}{\sqrt{x^2+y^2}} - \frac{x^2}{\bigl(x^2+y^2\bigr)^{3/2}} = \frac{ y^2 }{R^3} \\ \left. \partial_x f(x,y) \right\rvert_R &= \partial_x \left[ \frac{x}{R} \right]_R = \frac{1}{R} \end{align*}
A compact notation that allows us to state the expression of Equation 3.4.1 in a more transparent way is achieved as follows: We observe that the expressions in the sums amount to writing out in components a scalar product of $\mathbf q$ and $\dot{\mathbf q}$ with vectors that are obtained by the partial derivatives. These vectors are denoted gradients with respect to $\mathbf q$ and $\dot{\mathbf q}$, and they will be written as 1) \begin{align} \nabla\!_{\mathbf q}\, \mathcal C = \begin{pmatrix} \partial_{q_1} \mathcal C \\ \vdots \\ \partial_{q_D} \mathcal C \end{pmatrix} \qquad \text{and} \qquad \nabla\!_{\dot{\mathbf q}}\, \mathcal C = \begin{pmatrix} \partial_{\dot q_1} \mathcal C \\ \vdots \\ \partial_{\dot q_D} \mathcal C \end{pmatrix} \tag{3.4.2} \end{align} such that \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (\mathbf q(t) , \dot{\mathbf q}(t) ,t) &= \dot{\mathbf q} \cdot \nabla\!_{\mathbf q}\, \mathcal C + \ddot{\mathbf q} \cdot \nabla\!_{\dot{\mathbf q}}\, \mathcal C + \frac{\partial \mathcal{C}}{\partial t} \end{align*} In terms of the phase-space coordinates $\boldsymbol\Gamma = (\mathbf q, \dot{\mathbf q})$ one can also adopt the even more compact notation \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (\mathbf q(t) , \dot{\mathbf q}(t) ,t) &= \dot{\boldsymbol\Gamma} \cdot \nabla\!_{\boldsymbol\Gamma}\, \mathcal C + \frac{\partial \mathcal{C}}{\partial t} \end{align*} or even \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathcal{C} (\mathbf\Gamma(t) ,t) &= \dot{\boldsymbol\Gamma} \cdot \nabla\, \mathcal C (\mathbf\Gamma(t) ,t) + \frac{\partial \mathcal{C}}{\partial t} (\mathbf\Gamma(t) ,t) \end{align*} where the index of the nabla operator has been dropped with the understanding that it is clear from the context what the operator refers to. We make use of these derivatives while introducing some important physical quantities that are constants of the motion in specific settings.
3.4.1 The kinetic energy
When no forces are acting on a particle, $\mathbf F_{\text{tot}} = \mathbf 0$, it moves with constant velocity. All functions that depend only on the velocity will then be constant. In particular this holds for the kinetic energy, $T$, that will play a very important role in the following.
Theorem 3.2 Conservation of kinetic energy
The kinetic energy $T = \dfrac{m}{2}\ {\dot{\mathbf q}}^2$ of a particle is conserved
iff no net force acts on the particle, i.e., iff $\mathbf F_{\text{tot}} = \mathbf 0$.
Proof.
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d} t} T
& = \frac{m}{2} \; \frac{\mathrm{d}}{\mathrm{d} t}\; \sum_i \dot q_i \cdot \dot q_i
= m \; \sum_i \dot q_i \cdot \ddot q_i
\\
& = m \dot{ \mathbf q } \cdot \ddot {\mathbf q}
= \dot{\mathbf q} \cdot (m \: \ddot{\mathbf q})
= \dot{\mathbf q} \cdot \mathbf F_{\text{tot}}
= 0
\end{align*}
In the last two steps we used Newton's 2nd law,
and the assumption that $\mathbf F_{\text{tot}} = \mathbf 0$.
qed
3.4.2 Work and total energy
From a physics perspective, work is performed when a body is moved in the presence of an external force.
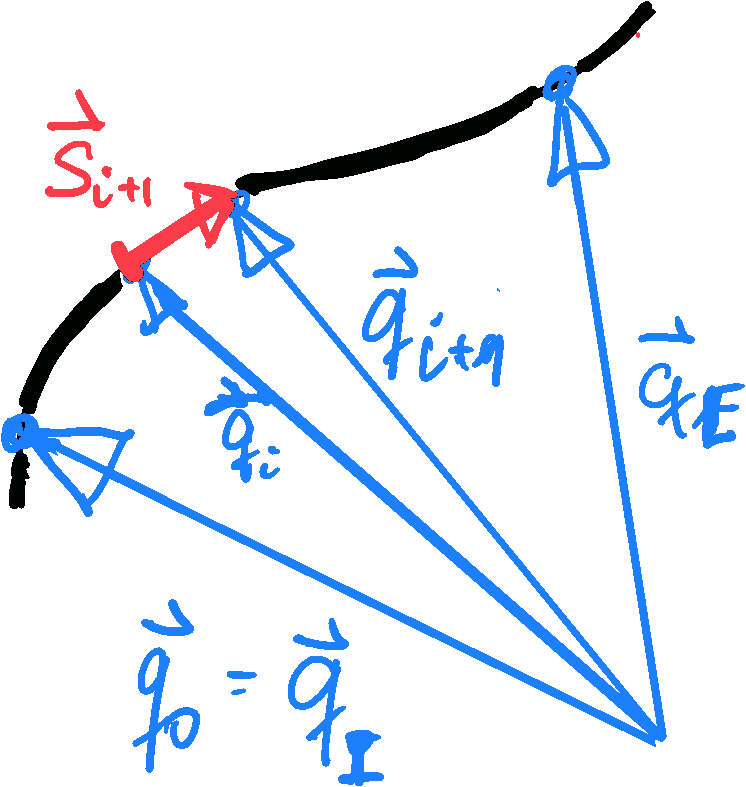 Figure 3.6: Breaking a particle track $\mathbf q(t)$ into a sequence of discrete points $\mathbf q_i$
with segments $\mathbf s_{i+1} = \mathbf q_{i+1} - \mathbf q_i$.}
Figure 3.6: Breaking a particle track $\mathbf q(t)$ into a sequence of discrete points $\mathbf q_i$
with segments $\mathbf s_{i+1} = \mathbf q_{i+1} - \mathbf q_i$.}
- When the force $\mathbf F$ is constant along a straight path of displacement $\mathbf s = \mathbf q_E - \mathbf q_I$, from a position $\mathbf q_I$ to the position $\mathbf q_E$, then the work $W$ amounts to the scalar product $W = \mathbf F \cdot \mathbf s$.
- When the force depends on the position along the path, we parameterize the motion along the path by time, $\mathbf q(t)$, with $\mathbf q(t_I) = \mathbf q_I$ and $\mathbf q(t_E) = \mathbf q_E$ and break it into sufficiently small pieces $\mathbf s_i = \mathbf q(t_i) - \mathbf q(t_{i} - \Delta t)$ where the force $\mathbf F_i = \mathbf F( t_i )$ and the velocity of the particle $\dot q(t_i)$ may be assumed to be constant, such that $\dot{\mathbf q}(t_i) = \bigl( \mathbf q(t_i) - \mathbf q(t_{i-1}) \bigr) / \Delta t$. Then
\begin{align*} W = \sum_i \mathbf F_i \cdot \mathbf s_i =\lim_{\Delta t \to 0} \sum_i \mathbf F_i \cdot \dot{\mathbf q} \; \Delta t = \int_{t_0}^{t_1} \mathbf F (t) \cdot \dot{\mathbf q} (t) \; \mathrm{d} t = \int_{\mathbf q (t)} \mathbf F \cdot \mathrm{d}\mathbf q \end{align*} The last equality should be understood here as a definition of the final expression that is interpreted here in the spirit of the substitution rule of integration. Moreover, $\mathbf F (t)$ denotes here the force acting on the particle at time $t$, where the particle is at the position $\mathbf q (t)$ and moving with velocity $\dot{\mathbf q} (t)$, i.e., one may also have $\mathbf F \bigl( \mathbf q(t) \bigr)$, or $\mathbf F \bigl( \mathbf q(t), \dot{\mathbf q} (t) \bigr)$, or an explicit time dependence on top of the dependence on the particle position.
Definition 3.5 Work and Line Integrals
The work, $W$, of a particle that performs a path $\mathbf q$ under the influence of a force $\mathbf F(t)$ amounts to the result of the line integral \begin{align*} W = \int_{\mathbf q} \mathbf F \cdot \mathrm{d}\mathbf q \\ \end{align*} When the path is parameterized by time, then $W$ amounts to the time integral of dissipated power $P(t) = \mathbf F (t) \cdot \dot{\mathbf q} (t)$, \[ W = \int \mathbf F (t) \cdot \dot{\mathbf q} (t) \; \mathrm{d} t = \int P(t) \; \mathrm{d} t \]
Remark 3.5. Here, $\mathbf F (t)$ denotes the force that is acting on the particle at time $t$, irrespective of how it emerges. Specifically, the time dependence of $\mathbf F (t)$ accounts for changes of the position $\mathbf q(t)$, the velocity $\dot{\mathbf q}(t)$, and any additional time dependences due to external incluences (if applicable).
Remark 3.6. The scalar product $\mathbf F \cdot \mathrm{d}\mathbf q$ or $P(t) = \mathbf F (t) \cdot \dot{\mathbf q} (t)$ singles out only the action of the force parallel to the trajectory. The perpendicular components do not perform work. Hence, a force that is always acting perpendicular to the velocity, i.e., perpendicular to the path of the particle, does not perform any work, \[ W = \int \mathbf F (t) \cdot \dot{\mathbf q} (t) \; \mathrm{d} t = \int 0 \; \mathrm{d} t = 0 \] It only changes the direction of motion.
Remark 3.7. The result of the integral does not rely on the parameterization of the path by time. For instance mathematicians prefer to use the length $\ell$ of the path. The speed of the particle is then $\dot \ell(t) = \left\lvert \dot{\mathbf q} (t) \right\rvert$ and one finds \[ W = \int \mathbf F (t) \cdot \mathrm{d}\mathbf q = \int \mathbf F (t(\ell)) \cdot \dot{\mathbf q} (t(\ell)) \; \frac{\mathrm{d} \ell}{\dot\ell} = \int \mathbf F (\ell) \cdot \frac{\mathrm{d}\mathbf q(\ell)}{\mathrm{d} \ell} \; \mathrm{d} \ell \] where $\mathrm{d}{\boldsymbol q} / \mathrm{d}\ell$ is a unit vector pointing in the direction of the trajectory.
Remark 3.8. Line integrals are also used to determine the length, $L$, of a path in space. After all, the length amounts to the time integral of the speed, $\dot\ell(t)$, and one has \begin{align*} % \label{eq:} L = \int\mathrm{d}\ell = \int \mathrm{d} t \: \dot\ell(t) = \int \mathrm{d} t \: \frac{\dot{\mathbf q}^2(t)}{\dot\ell(t)} = \int \mathrm{d} \vec q \cdot \frac{\dot{\mathbf q}(t)}{\dot\ell(t)} = \int \mathrm{d} \vec q \cdot \frac{\mathrm{d} \vec q(\ell)}{\mathrm{d}\ell} \end{align*} This is further illustrated in Problem 3.22.
The calculation of work simplifies dramatically when the force can be written as gradient of another function, $\Phi$.
Definition 3.6 Potentials and Conservative Forces
A force $\mathbf F (\mathbf q)$ that can be expressed as the negative gradient of a function $\Phi (\mathbf q)$, \begin{align*} \mathbf F (\mathbf q) = - \nabla \Phi (\mathbf q) = -\ \begin{pmatrix} \partial_{q_1} \Phi( q_1, \dots, q_D) \\ \vdots \qquad\qquad \qquad \\ \partial_{q_D} \Phi( q_1, \dots, q_D) \end{pmatrix} \end{align*} is called a conservative force and the function $\Phi$ is the potential associated to the force.
Remark 3.9. Conservative forces only depend on position, $\mathbf F = \mathbf F (\mathbf q)$. They neither explicitly depend on time nor on the velocity $\mathbf q$.
Example 3.8 Conservative forces: (counter-)examples
- Gravitational acceleration $\mathbf g$ is is constant in space. Hence, gravity is a conservative force.
- Friction of a cube sliding over a table is proportional to the particle speed $v$. Therefore, friction is not a conservative force.
- Setting the rope into motion for rope skipping requires an oscillatory force. Due to its time time dependence such a force is not conservative.
Theorem 3.3 Work for conservative forces
For conservative forces, $\mathbf F = -\nabla\Phi(\mathbf q)$,
the work for a path
$\mathbf q(t)$ from $\mathbf q_0$ to $\mathbf q_1$
amounts to the difference of the potential evaluated at the initial and at the final point of the path
\begin{align*}
W = \int_{\mathbf q(t)} \mathbf F \cdot \mathrm{d} \mathbf q
= \Phi( \mathbf q_0 ) - \Phi( \mathbf q_1 )
\end{align*}
Proof.
\begin{align*}
W
&= \int_{t_0}^{t_1} \mathbf F \cdot \dot{\mathbf q} \; \mathrm{d} t
= - \int_{t_0}^{t_1} \nabla \Phi \cdot\dot{\mathbf q} \; \mathrm{d} t
\\
&= - \int_{t_0}^{t_1}
\sum_i \frac{\partial \Phi} {\partial q_i}\; \frac{\partial q_i}{\partial t} \; \mathrm{d} t
= -\int_{t_0}^{t_1} \frac{\mathrm{d}\ \Phi}{\mathrm{d} t}\; \mathrm{d} t
\\
& = - \bigl( \Phi( \mathbf q(t_1)) - \Phi( \mathbf q(t_0)) \bigr)
= \Phi (\mathbf q_0) - \Phi( \mathbf q_1)
\\
\end{align*}
qed
Remark 3.10. The work performed along a closed path vanishes for conservative forces. After all, in that case $\mathbf q_1 = \mathbf q_0$ such that $W = \Phi (\mathbf q_0) - \Phi( \mathbf q_1) = 0$.
Remark 3.11. The potential in itself is not an observable. 2) One can only observe the work, which is the potential difference between two positions, and the force, which is the negative gradient of the potential. Therefore, the potential is only defined up to adding a constant.
Example 3.9 Gravitational Potential
For a particle of mass $m$ gravity on the Earth surface
gives rise to a force of magnitude $\mathbf F(x,y,z) = -m\, g\, \hat{\boldsymbol z}$
that can be derived from the potential $\mathbf \Phi(x,y,z) = m\,g\,z$,
\begin{align*}
- \nabla \Phi_1(x,y,z)
= \begin{pmatrix}
-\partial_x \Phi(x,y,z) \\
-\partial_y \Phi(x,y,z) \\
-\partial_z \Phi(x,y,z)
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0 \\
-m\, g
\end{pmatrix}
= \mathbf F(x,y,z)
\end{align*}
Far away, at a position $\mathbf q = (q_1, q_2, q_3)$ from the center of
Earth,
gravity induces a force $\mathbf F(\mathbf q) = - G \, M_E \, m \, \mathbf q / \lvert \mathbf q \rvert^3$
on a
body of mass $m$. This force can be obtained as
\begin{align*}
-\nabla \phi_2(\mathbf q)
= \nabla \frac{G \, M_E \, m}{ \sqrt{ q_1^2 + q_2^2 + q_3^2 } }
= G \, M_E \, m \:
\begin{pmatrix}
\partial_{q_1} \frac{1}{ \sqrt{ q_1^2 + q_2^2 + q_3^2 }} \\
\partial_{q_2} \frac{1}{ \sqrt{ q_1^2 + q_2^2 + q_3^2 }} \\
\partial_{q_3} \frac{1}{ \sqrt{ q_1^2 + q_2^2 + q_3^2 }}
\end{pmatrix}
\\
= G \, M_E \, m \:
\begin{pmatrix}
\frac{ -q_1 }{ \left[ q_1^2 + q_2^2 + q_3^2 \right]^{3/2} } \\
\frac{ -q_2 }{ \left[ q_1^2 + q_2^2 + q_3^2 \right]^{3/2} } \\
\frac{ -q_3 }{ \left[ q_1^2 + q_2^2 + q_3^2 \right]^{3/2} }
\end{pmatrix}
= \frac{ - G \, M_E \, m }{ \left[ q_1^2 + q_2^2 + q_3^2 \right]^{3/2} } \: \mathbf q
= \mathbf F(\mathbf q)
\end{align*}
Remark 3.12.
According to Theorem 3.3 differences of the value of the potential between two positions
amount to the work performed in the potential.
Different approaches to calculate the value of this scalar observable must yield identical results.
Therefore, the functional dependence of the potential must not depend on the choice of the coordinate system.
This invariance requires that the potential can always be expressed in terms of scalar products.
For the potentials in Example 3.9 this is achieved by writing
\begin{align*}
\Phi_1( \mathbf q ) &= m \, \mathbf g \cdot \mathbf q
\quad\text{ with }\quad \mathbf g = (0,0,-g)
\Phi_2 ( \mathbf q ) &= - G \, M_E \, m / \sqrt{ \mathbf q \cdot \mathbf q }
\end{align*}
Remark 3.13. One can make use of the properties of scalar products to reduce the computational work to determine the force for a given potential by working out the component $i$ of the gradient where $i$ is can be any index of the vector. For conciseness we also write then $\partial_i$ for the partial derivative with respect to component $q_i$ of the argument $\mathbf q$ of $\Phi(\mathbf q)$. For the potentials in Example 3.9 this works as follows \begin{align*} &-\partial_i \Phi_1( \mathbf q ) = -m \, \partial_i \sum_j g_j q_j = -m \, \sum_j g_j \delta_{ij} = -m g_i\\ &-\partial_i \Phi_2( \mathbf q ) = G \, M_E \, m \: \partial_i \Bigl[ \sum_j q_j^2 \Bigr]^{-1/2} = \frac{ - G \, M_E \, m \, q_i }{ \Bigl[ \sum_j q_j^2 \Bigr]^{3/2} } \end{align*} In particular in the second case the advantage is evident.
Example 3.10 Falling men and cat
When a cat, that has a mass of $m = 3 \, \text{kg}$, falls from a balcony in the fourth floor, i.e., from a height $H \simeq 4 \times 3 \, \text{m} = 12 \, \text{m}$, the initial potential energy
\begin{align*} V_{\text{cat}} = mgH = 3 \, \text{kg} \times 10 \, m/s^2 \times 12 \, m = 360 \, \text{kg} m^2/s^2 \end{align*}
will be transformed into kinetic energy and then dissipated when the cat hits the ground. To get an idea about this energy we compare it to the energy dissipated when a man of mass $M = 80 \, \text{kg}$, falls out of his bed that has a height of $h = 50 \, cm$,
\begin{align*} V_{\text{man}} = Mgh = 80 \, \text{kg} \times 10 \, m/s^2 \times 0.5 \, m = 400 \, \text{kg} m^2/s^2 \end{align*}
From the point of view of the dissipated energy the fall of the cat is not as bad as it looks at first sight.
Conservative forces are called conservative forces because motion in such a potential conserves the sum of the potential energy and the kinetic energy.
Theorem 3.4 Conservation of the total energy
The total energy $E= T + \Phi$ of a particle is conserved
if it moves in a conservative force field $\mathbf F = - \nabla\Phi$.
Proof.
\begin{align*}
\frac{\mathrm{d} E}{\mathrm{d} t}
& = \frac{\mathrm{d} T}{\mathrm{d} t} + \frac{\mathrm{d} \Phi}{\mathrm{d} t}
= m\ \dot{\mathbf q} \cdot \ddot{\mathbf q}\ + \nabla\Phi \cdot \dot{\mathbf q}
= \dot{\mathbf q} \cdot \underset{=\ \mathbf 0}{\underbrace{\big( m \ddot{\mathbf q} - \mathbf F \big)}}
=\ \mathbf 0
\end{align*}
In the third equality we used that the force is conservative,
and in the final step, we used Newton's second law which states that $m \ddot{\mathbf q} = \mathbf F$.
qed
Example 3.11 Accidents at work and on the street
A paramedic emergency ambulance receives two calls from an accident site:
i. a craftsmen fell from a roof of height $H$
ii. a teenager hit a tree with his motorcycle with a speed $v$
For which height does the energy of the craftsman approximately match
the one of the motor cyclist when he drove
- in the city, $v_C = 50 \, \text{km / h}$,
- outside the city, $v_L = 100 \, \text{km / h}$,
- on a German autobahn with $v_A = 150 \, \text{km / h}$
- or was really speeding with $v_S = 200 \, \text{km / h}$.
We assume that they both have comparable mass. Energy conservation entails that we have to compare the potential energy $V_{\text{worker}}$ of the craftsman on the roof and the kinetic energy of the teenager on the motorcycle $T_{\text{teenager}}$, \begin{align*} mgH = V_{\text{worker}} = T_{\text{teenager}} = \frac{m}{2} \, v^2 \quad\Leftrightarrow\quad H = \frac{ v^2 }{ 2 g } \end{align*} Hence we find \begin{align*} \begin{array}{lllll} v & 50 \, \text{km / h} & 100 \, \text{km / h} & 150 \, \text{km / h} & 200 \, \text{km / h} \\ H & 12 \, \text{m} & 50 \, \text{m} & 110 \, \text{m} & 200 \, \text{m} \\ \text{floor} & 4 & 16 & 36 & 64 \\ \end{array} \end{align*} Most likely, the teenager will encounter more severe injuries, unless the craftsman is working on a really high building.
3.4.3 Momentum
Theorem 3.5 Conservation of momentum
The momentum $\mathbf P = \sum_{i=1}^N m_i \dot{\mathbf q}_i(t)$ of a set of $N$ particles with masses $m_i$ that reside at the positions $\mathbf q_i(t)$ is conserved if no net force $\mathbf F_{\text{tot}}$ acts on the system.
Proof. The time derivative of the total momentum is $\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} \mathbf P = \sum_{i=1}^N m_i \ddot{\mathbf q}_i(t)$ where $m_i \ddot{\mathbf q}_i(t)$ amounts to the force on particle $i$. This force amounts to the sum of an external force $\mathbf F_i$ on particle $i$ and the forces $\mathbf f_{ji}$ exerted by other particles $j$ on $i$. The net force amounts to the sum of the external forces, $\mathbf 0 = \mathbf F_{\text{tot}} = \sum_i \mathbf F_i$. Newton's third law requires that $\mathbf f_{ji} = -\mathbf f_{ij}$, and we will set $\mathbf f_{ii} = \mathbf 0$ to simplify notations of indices in the sums. Consequently, \begin{align*} \frac{\mathrm{d}}{\mathrm{d} t} \mathbf P = \sum_{i=1}^N \left( \mathbf F_i + \sum_{j=1}^N \mathbf f_{ji} \right) &= \sum_{i=1}^N \mathbf F_i + \sum_{i=1}^N \sum_{j=1}^N \mathbf f_{ij} \\ &= \mathbf F_{\text{tot}} + \frac{1}{2} \; \sum_{i=1}^N \sum_{j=1}^N \bigl( \mathbf f_{ij} + \mathbf f_{ji} \bigr) = \mathbf 0 \end{align*} qed
 Фабрицио, CC BY-SA 4.0
Figure 3.7: Newton's cradle.
When the excited ball to the right is released it will come down,
hit the rightmost ball that is hanging down at rest.
The momentum is transferred to the leftmost ball,
and that is moving up (almost) as far to the left
as the initial ball was excited to the right.
Its motion reverses,
and by the same sequence of events the motion proceeds from left to right.
Фабрицио, CC BY-SA 4.0
Figure 3.7: Newton's cradle.
When the excited ball to the right is released it will come down,
hit the rightmost ball that is hanging down at rest.
The momentum is transferred to the leftmost ball,
and that is moving up (almost) as far to the left
as the initial ball was excited to the right.
Its motion reverses,
and by the same sequence of events the motion proceeds from left to right.
Example 3.12 One-dimensional collisions
We consider two steel balls that can freely move along a line.
They have masses $m_1$ and $m_2$ and reside at positions $x_1$ and $x_2$, respectively.
Initially ball two is at rest in the origin, and ball one is approaching from the right with a constant speed $v_1$.
What is the speed of the balls after the collision?
Before and after the collision the particles feel no forces such that their velocity is constant.
We assume that the collision is elastic such that energy is preserved.
Hence,
\begin{align*}
\text{ before collision } \quad
&= \quad \text{after collision}
\\
\text{momentum:} \qquad\qquad
m_1 \, v_1
\quad&=\quad m_1 \, v_1' + m_2 \, v_2'
\\
\text{energy:} \qquad\qquad
\frac{m_1}{2} \, v_1^2
\quad&=\quad \frac{m_1}{2} \, (v_1')^2 + \frac{m_2}{2} \, (v_2')^2
\end{align*}
where the prime indicates the post-collision velocities.
These velocities can best be determined by writing the momentum and energy balance in the form
\begin{align*}
m_1 \, ( v_1 - v_1' ) = m_2 \, v_2'
\quad\text{and}\quad
m_1 \, ( v_1^2 - v_1'^2 ) = m_2 \, v_2'^2
\end{align*}
and dividing the second by the first equation.
This provides
\begin{align*}
v_1 + v_1' = v_2'
\end{align*}
Together with the momentum balance it provides
\begin{align*}
v_1' = \frac{ m_1 - m_2 }{ m_1 + m_2 } \; v_1
\qquad\text{and}\qquad
v_2' = \frac{ 2 \, m_1 }{ m_1 + m_2 } \; v_1
\end{align*}
In particular, when the two particles have the same mass one obtains that
$v_1'= 0$ and $v_2' = v_1$
which is beautifully exem-\\plified by the dynamics of Newton's cradle.
3.4.4 Angular Momentum
In the immediate vicinity of the collisions the balls in Newton's cradle perform a motion along a horizontal line, as discussed in Example 3.12. However, during the excursions to the left and right they follow a circular track where the chains act as arms and their suspension as fulcrum of the circular motion. In such settings it is often desirable to also consider the evolution of the angular momentum.
Theorem 3.6 Conservation of angular momentum
The angular momentum $\mathbf L = \sum_{i=1}^N m_i \mathbf q_i(t) \times \dot{\mathbf q}_i(t)$ of a set of $N$ particles with masses $m_i$ that reside at the positions $\mathbf q_i(t)$ is conserved if no external forces act on the system and if the interaction forces between pairs of particles act parallel to the line connecting the particles.
Proof.
\begin{align*}
\frac{\mathrm{d}}{\mathrm{d} t} \mathbf L
&= \sum_{i=1}^N m_i \Bigl( \dot{\mathbf q}_i(t) \times \dot{\mathbf q}_i(t)
+ \mathbf q_i(t) \times \ddot{\mathbf q}_i(t) \Bigr)
\\
&= \sum_{i<j} \Bigl( \mathbf q_i(t) \times \mathbf f_{ij} + \mathbf q_j(t) \times \mathbf f_{ji} \Bigr)
\\
&= \sum_{i<j} \Bigl( \mathbf q_i(t) - \mathbf q_j(t) \Bigr) \times \mathbf f_{ij}
= \mathbf 0
\end{align*}
where we used that $\mathbf f_{ij} = - \mathbf f_{ji}$ due to Newton's third law,
and that $(\mathbf q_i(t) - \mathbf q_j(t) )$ is parallel to $\mathbf f_{ij}$ by assumption on the particle interactions.
qed
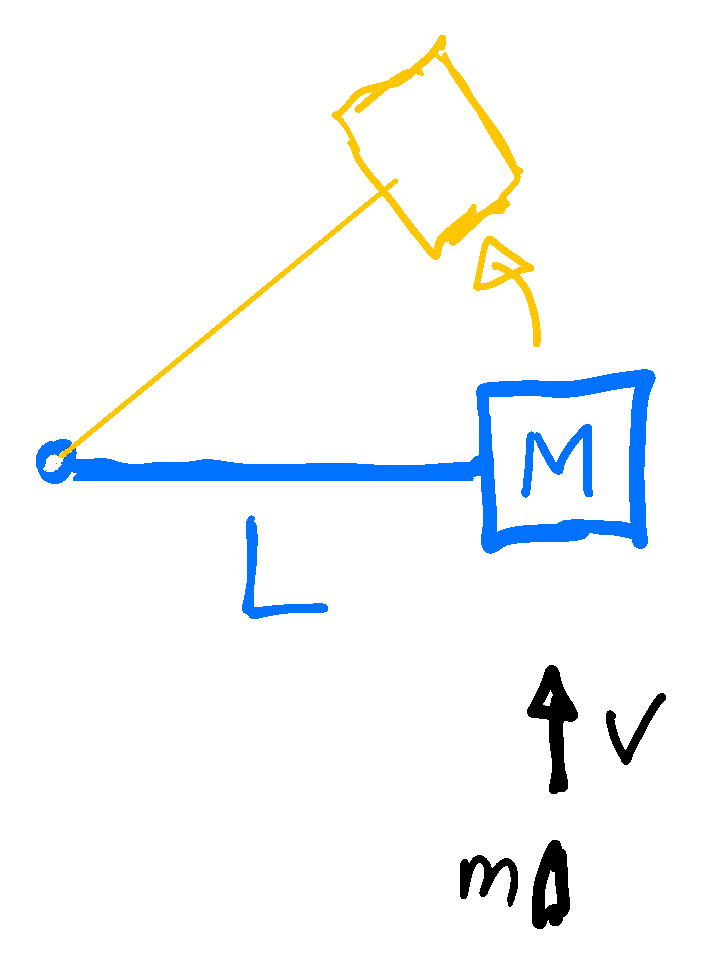 Figure 3.8: Notations adopted in the measurement of the speed $v$ of a bullet of mass $m$
that is hitting a rotor of mass $M$ attached to an arm of length $L$;
see Example 3.13.
Figure 3.8: Notations adopted in the measurement of the speed $v$ of a bullet of mass $m$
that is hitting a rotor of mass $M$ attached to an arm of length $L$;
see Example 3.13.
Example 3.13 Determine the speed of a bullet.
In a CSI lab one tests the speed of a bullet by shooting it into a rotor where a mass $M=1 \, \text{kg}$ can move horizontally with minimal fraction on an arm with length $L=1 \, \text{m}$. For a bullet of a mass $m=8 \, \text{g}$ we find a rotation frequency $f = 0.16 \,Hz$. What is the muzzle velocity $v$ of the gun? During the collision the bullet gets stuck in the rotor mass. Before and after the collision the angular momentum thus is \begin{align*} m \, L \, v &= (m+M) \, L^2 \, \omega = (m+M) \, L^2 \, 2\pi\, f \\ \Leftrightarrow\qquad v &= \frac{ m+M }{m} \: 2\pi \, f \, L = \frac{ 1008 }{ 8 } \times 2\pi \times 0.16 \, \text{m/s} \simeq 125 \, \text{m/s} \end{align*}
3.4.5 Self Test
Problem 3.7: Derivatives of common composite expressions
Evaluate the following derivatives.
- $\frac{\mathrm{d}}{\mathrm{d} x} ( a + x )^b$
- $\frac{\partial}{\partial x} ( x + b \, y )^2$
- $\frac{\mathrm{d}}{\mathrm{d} x} ( x + y(x) )^2$
- $\frac{\mathrm{d}}{\mathrm{d} t} \sin \theta(t)$
- $\frac{\mathrm{d}}{\mathrm{d} t} \bigl( \sin\theta(t) \; \cos\theta(t) \bigr)$
- $\frac{\mathrm{d}}{\mathrm{d} t} \sin\bigl( 2 \theta(t) \bigr)$
- $\frac{\mathrm{d}}{\mathrm{d} z} \sqrt{a + b \, z^2}$
- $\frac{\partial}{\partial x_3} \left[ \sum_{j=1}^6 x_j^2 \right]^{-1/2}$
- $\frac{\partial}{\partial y_1} \ln( \mathbf x \cdot \mathbf y )$
In these expressions $a$ and $b$ are real constants, and $\mathbf x$ and $\mathbf y$ are 6-dimensional vectors.
Problem 3.8:
Running mothers
Demonstrate that
\begin{align*}
I = \dot x_1(t) \: \dot x_2(t) + \omega^2 \; x_1(t) \: x_2(t)
\end{align*}
is a constant of motion of a two-dimensional harmonic oscillator with equation of motion
\begin{align*}
\ddot{\mathbf x} (t) = - \omega^2 \: \mathbf x (t)
\qquad \text{with } \quad
\omega \in \mathbb R
\quad \text{and} \quad
\mathbf x (t) = \bigl( x_1(t), x_2(t) \bigr) \in \mathbb R^2
\end{align*}
Problem 3.9:
Anvil shooting
Anvil shooting is a tradition in some US communities to celebrate St.Clement's Day, honoring Pope Clement I, the patron saint of blacksmiths and metalworkers. Typical anvils have a mass of about $150 \, \text{kg}$ and they are shot up to a height of $60 \, \text{m}$. Which energy must the gun powder release to the anvil for such a feat?
Problem 3.10:
Running mothers
In the Clara Zetkin Park one regularly encounters
blessings3) of dozens of mothers jogging in the park while pushing baby carriages.
Troops of kangaroo mothers rather carry their youngs in pouches.
- Estimate the energy consumption spend in pushing the carriages as opposed to carrying the newborn.
The carriages suffer from friction. Let the friction coefficient be $\gamma=0.3$.
When carrying the baby the kangaroo must lift it up in every jump and the associated potential energy is dissipated. - How does the running speed matter in this discussion?
- How does the mass of the babies/youngs make a difference?
Problem 3.11:
The sledgehammer experiment
In his magnificent book “Thinking Physics” Lewis Carroll (Epstein (2009)) sets out a class room experiment that he used to perform in his physics class:
He placed an anvil on his chest and
asked a student from the audience to hit the anvil with a sledge hammer
as hard as he could manage.
What will happen?4)
Problem 3.12:
The rotating chair experiment
The spin increases when an ice dancer pulls inwards arms and legs.
This is illustrated in the picture of Yuko Kawaguti in the margin,
and the physical principle has beautifully been demonstrated in a
wikimedia movie
by Oliver Zajkov from the Physics Institute at the University of Skopje.
- Assume that a less careful experimenter starts his motion with a spin of $1 \, \text{Hz}$, holding $5 \, \text{kg}$ barbells with stretched-out arms $1 \, \text{m}$ away from the rotation axis.
Estimate his spin rate when he pulls in his arms till the barbells reach a distance of $20 \, \text{cm}$ from the rotation axis. - Which trajectory will they take when the careless experimenter gets dizzy and looses hold on the barbells?


